C#下的摄像机标定

前言：计算机视觉的基本任务之一是从摄像机获取的图像信息出发计算三维空间中物体的几何信息，并由此重建和识别物体，而空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系是由摄像机成像的几何模型决定的，这些几何模型参数就是摄像机参数。在大多数条件下，这些参数必须通过实验与计算才能得到，这个过程称为摄像机标定。标定过程就是确定摄像机的几何和光学参数、摄像机相对于世界坐标系的方位。

内容：

      1.假设摄像机所拍摄到的图像与三维空间中的物体之间存在以下一种简单的线性关系：[像]=M[物]，这里，矩阵M可以看成是摄像机成像的几何模型。 M中的参数就是摄像机参数。通常参数分为摄像机的内参和外参。

      2.摄像机的标定方法分为三类：传统摄像机标定方法、主动视觉摄像机标定方法、摄像机自标定方法。

       传统的摄像机标定方法：特点：利用已知的景物结构信息，常用到标定块；优点：可以使用于任意的摄像机模型，标定精度高；不足：标定过程复杂，需要高精度的已知结构信息，在实际应用中很多情况下无法使用标定块。

       主动视觉摄像机标定方法：特点：已知摄像机的某些运动信息；优点：通常可以线性求解，鲁棒性比较高；不足：不能用于摄像机运动未知和无法控制的场合。

       摄像机自标定方法：特点：仅依靠多幅图像之间的对应关系进行标定；优点：仅需要建立图像之间的对应，灵活性强，潜在应用范围广；不足：非线性标定，鲁棒性不高。

       3.摄像机成像模型：图像是空间物体通过成像系统在平面上的反映，即空间物体在像平面上的投影。图像上每一个像素点的灰度反映了空间物体表面某点的反射光的强度，而该点在图像上的位置则与空间物体表面对应点的几何位置有关。这些位置的相互关系由摄像机成像系统的几何投影模型所决定，理想的成像模型是光学中的中心投影，也成为针孔模型，即假设物体表面的反射光都经过一个针孔而投影到像平面上，也就是满足光的直线传播条件。小孔成像透光量太小，需要长时间的曝光，实际摄像系统通常都由透镜或者透镜组组成。由于透镜设计的复杂性和工艺水平等影响，实际透镜成像系统不可能严格满足针孔模型，这也就产生了所谓的镜头畸变，常见的如径向畸变、切向畸变、薄棱镜畸变等，在远离图像中心处会有较大的畸变，在精密视觉测量等应用方面，应该尽量采用非线性模型来描述成像关系。

       4.常用坐标系及其关系：计算机视觉常用坐标系采用右手准则来定义，通常有三个不同层次的坐标系统：世界坐标系、摄像机坐标系、图像坐标系（图像像素坐标系、图像物理坐标系）。如下图所示：

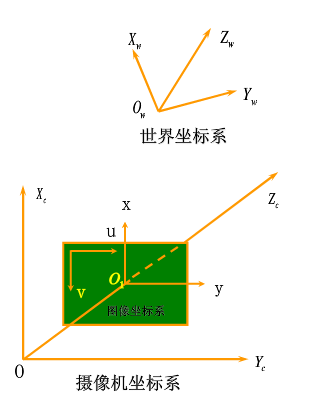
        （1）世界坐标系（O_w-X_w,Y_w,Z_w）：是客观世界的绝对坐标，由用户任意定义的三维空间坐标系，一般的3D场景都用这个坐标系来表示。

        （2）摄像机坐标系（O_c-X_cY_cZ_c）：以小孔摄像机模型的聚焦中心为原点，以摄像机光轴zc轴建立的三维直角坐标系。x，y一般与图像物理坐标系x_f，y_{f平行，且采取前投影模型。}

         （3）理想图像坐标系（O_i-X_uY_u）

         （4）实际图像坐标系（O_i-X_dY_d）

　　　　世界坐标系变为摄像机坐标系（三维空间刚体位置的变换）：

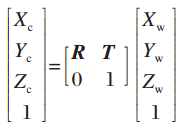　　　　，式中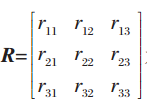：为旋转矩阵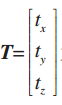；为平移矩阵。

　　　　摄像机坐标系变为理想图像坐标系（投影变换）：

　　　　

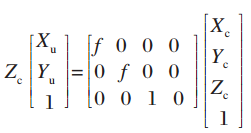
　　　　理想图像坐标系变为实际图像坐标系（考虑畸变）：镜头的畸变主要由径向畸变引起，二级径向畸变的镜头模型为：

　　　　

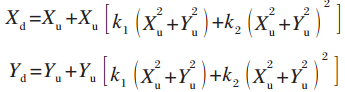
　　　　用齐次坐标表示为：

　　　　

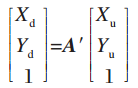
　　　　式中：k₁和k₂为径向畸变系数；A'为两者等效变换矩阵。

　　　　实际图像坐标变换为像素图像坐标：

　　　　

　　　　用齐次坐标表示为：

　　　　

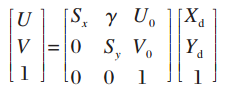
　　　　式中：（U₀，V₀）为图像中心O₁在O-UV中的坐标；S_x、S_y分别为图像平面上X、Y轴方向单位距离上的像素数；γ为两坐标轴间的倾斜因子。

　　　　由上面的公式可以得到：

　　　　

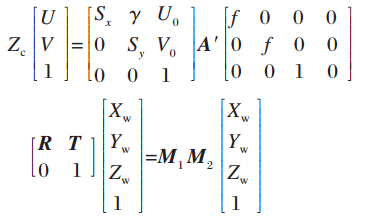
　　　　式中：M₁由S_x，S_y，U₀，V₀，f，k₁，k₂确定，只与摄像机本身的性质有关，这些参数为摄像机的内部参数；M₂由旋转矩阵R和平移向量T确定，为摄像机的外部参数。

　　以上就是标定算法的核心部分。在EMGU中使用CameraCalibration来完成对摄像头的标定，得到内参及外参。

　　代码后期附上：