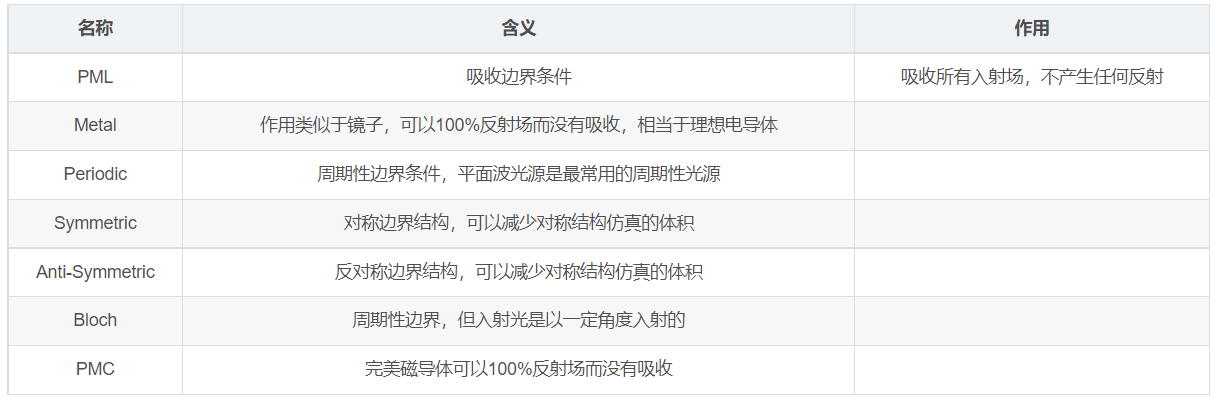
| 符号 | 名称 | SI量纲 | 含义 |
|---|---|---|---|
| E | 电场强度 | V/m | qE=电荷上的电力 |
| D | 电激发 | As/m^2 | 产生场的电荷是这个场的源 |
| P | 极化 | As/m^2 | 偶极矩/体积 |
| B | 磁场强度 | T(特斯拉)=Vs/m^2 | q(v×B)=作用于以速度v运动的电荷q上的磁力 |
| H | 磁激发 | A/m | 产生场的电流是这个场的涡* |
| M | 磁化 | A/m | 磁矩/体积 |
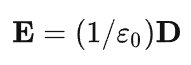
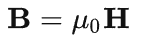
量为电荷量，电荷越多，D场越大；强度是对测试电荷的作用强度，D场越大，引起的E场越大，作用越强。D是电荷多少的描述，E是作用强度的描述
有关总场以及边界效应的概念详见知乎文章 总场－散射场边界的意义和使用相关(1) - 知乎 (zhihu.com)
边界条件详见B站视频《电磁场与电磁波》电磁场的边界条件_哔哩哔哩_bilibili
《电磁场与电磁波（第五版）》讲解视频 第九讲_哔哩哔哩_bilibili
什么是电磁场的边界条件？
边界条件是不同媒质的分界面上两侧的电磁场矢量之间满足的关系，是电磁场在不同媒质分界面上的基本属性。
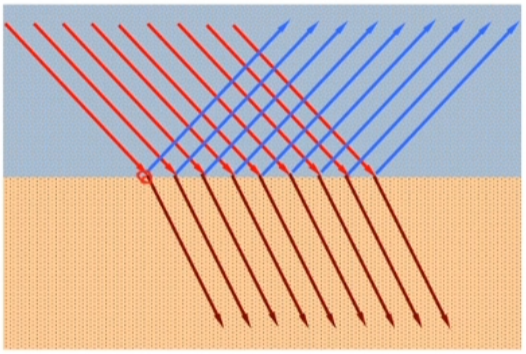
为什么要研究边界条件?
物理:两种不同媒质的分界面两侧的媒质的电磁特性参数发生突变，导致分界面两侧的电磁场也会产生突变。
数学:麦克斯韦方程组是微分方程组，其解是不确定的，边界条件起定解的作用。
如何确定边界条件?
麦克斯韦方程组的积分形式在不同媒质的分界面上仍然适用，由此出发可导出电磁场矢量在不同媒质分界面上的边界条件
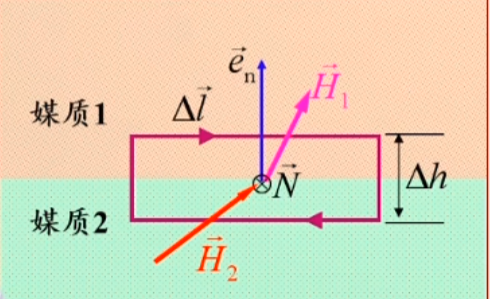
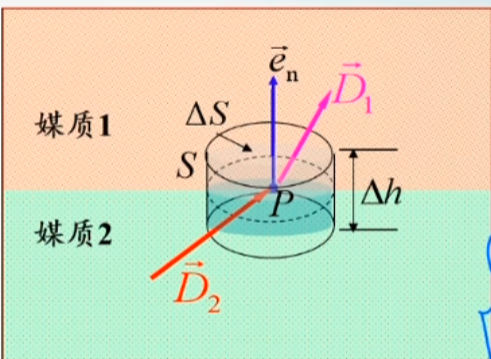
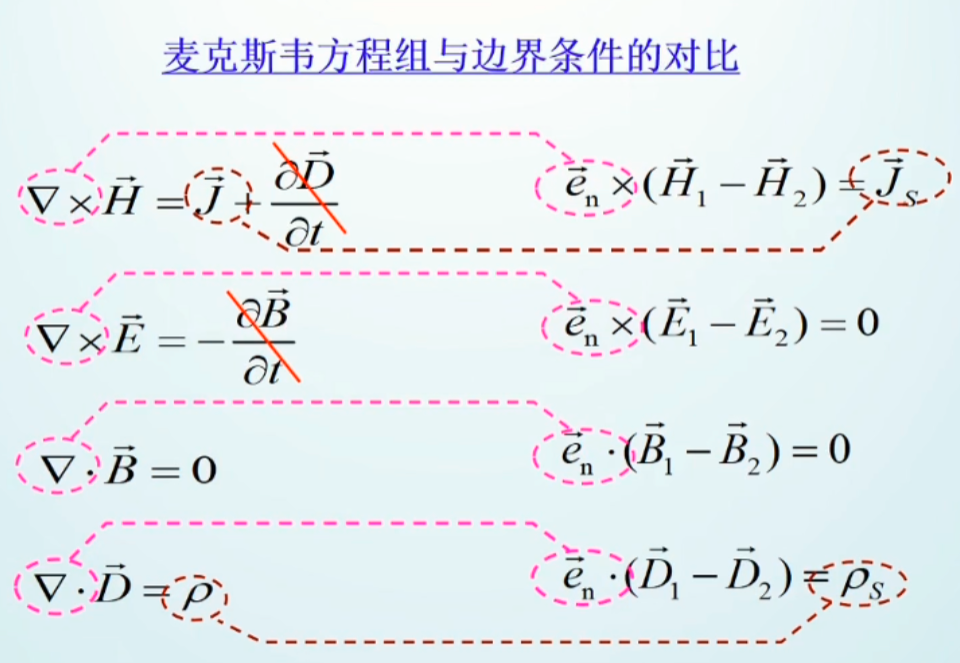
边界条件的普通表达形式
J为分界面上的自由面电流密度
ρ为分界面上的自由电荷面密度
推导
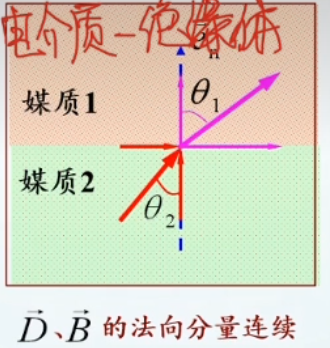
电磁场量的法向量边界条件
以分界面为界限，将空间分为上下两个不同介质，每个介质内的不同电场磁场的向量都可以分为以分界面法向量以及切面向量的两个向量，由此可以引出两个边界条件：法向边界条件、切向边界条件
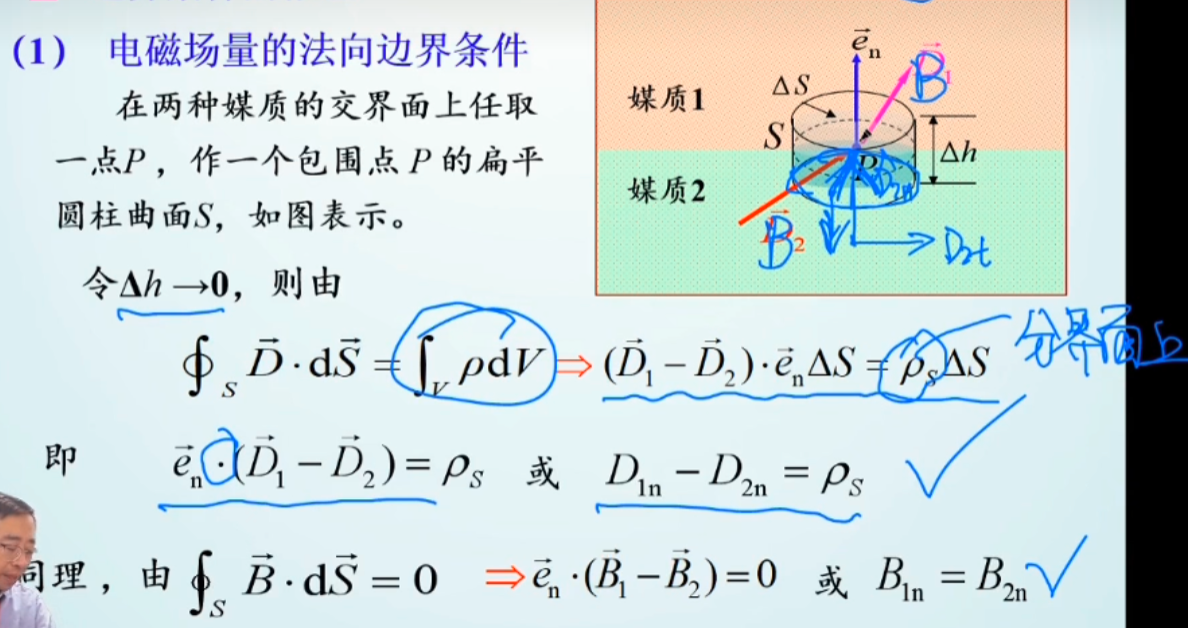
封闭曲面积分=上盖面积分+下底面积分+侧面积分 侧面与法向量正交则侧面积分为0，下盖方向与法向量方向相反则积分为负号
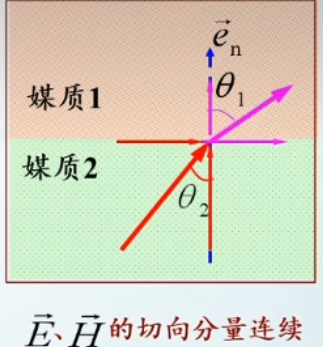
电磁场量的切向边界条件
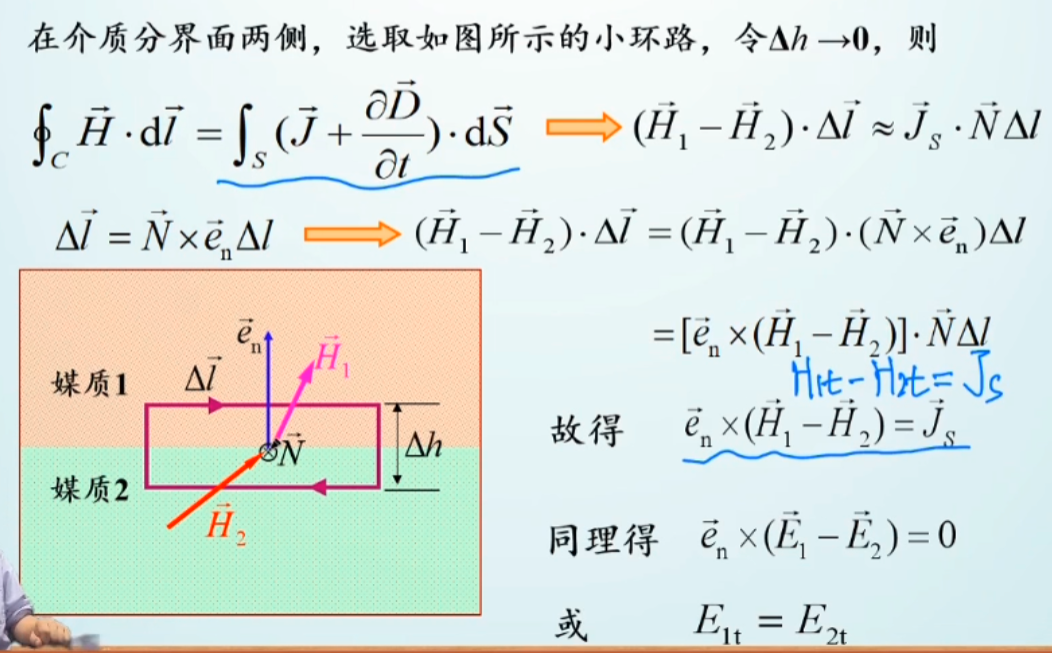
总结
- 电场切向分量连续——对于点来说没有旋度
- 磁场法向分量连续——磁通连续性定理决定
- 电场法相分量不连续
- 磁场切向分量不连续
几种常见的情况
理想介质
电介质指的是绝缘体，例如土壤和玻璃硅胶 电导率σ为0的为理想介质
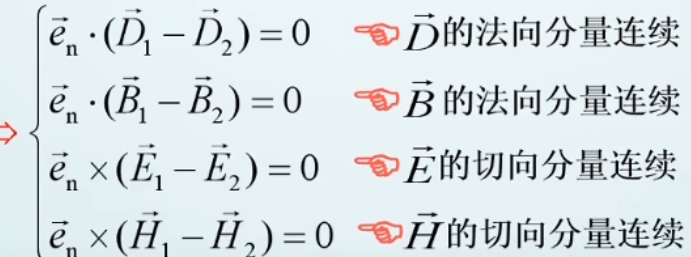
理想导体
首先需要明确一个概念：电导率σ为无穷大的为理想导体，理想导体在电场作用下会达到静电平衡，整个导体表面会形成等势面，导体内部处处电场磁场为零
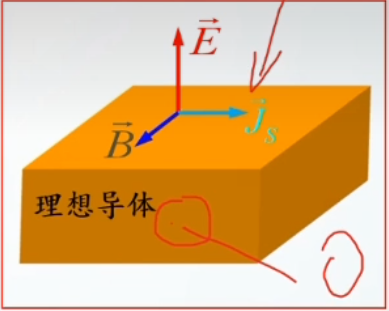
理想导体：电导率σ为无穷大的导电媒质
特点：时变情况下，理想导体内部电磁场为零
en表示垂直于分界面的向量即法向量；点乘为同向即法向向量；叉乘为垂向即切向向量
电立不躺：电场线永远垂直于导体（处于静电平衡）表面——等势面，数学表达也就是梯度（电场线）永远垂直于等值面（等势面）
磁躺不立：磁场只有切向量没有法向量
电壁：电导率σ为无穷大的材料表面（更多研究）
磁壁：磁导率μ为无穷大的材料表面
导电媒质 (0＜σ＜∞)
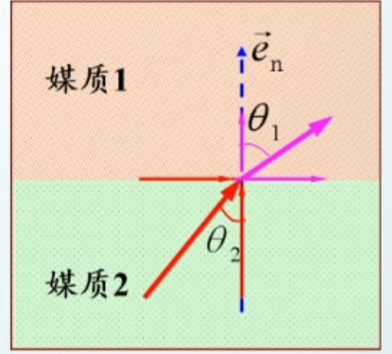
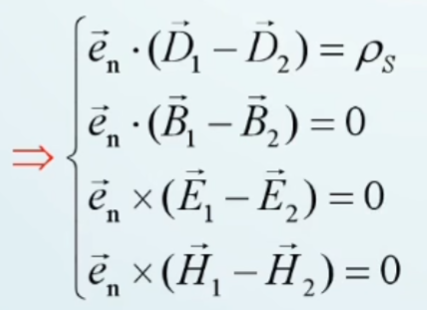
在导电媒质的分界面上，不存在面电流，即Js=0，但是可以存在面电荷，即ρs≠0
posted on
