截图选自Understanding the Finite-Difference Time-Domain Metho 作者是John B. Schneider
有限差分时域（FDTD）方法使用有限差分作为麦克斯韦方程组（特别是安培定律和法拉第定律）的近似。
麦克斯韦方程组乃是由四个方程共同组成的：
- 高斯定律：该定律描述电场与空间中电荷分布的关系。电场线开始于正电荷，终止于负电荷（或无穷远）。计算穿过某给定闭曲面的电场线数量，即其电通量，可以得知包含在这闭曲面内的总电荷。更详细地说，这定律描述穿过任意闭曲面的电通量与这闭曲面内的电荷之间的关系。
- 高斯磁定律：该定律表明，磁单极子实际上并不存在。所以，没有孤立磁荷，磁场线没有初始点，也没有终止点。磁场线会形成循环或延伸至无穷远。换句话说，进入任何区域的磁场线，必需从那区域离开。以术语来说，通过任意闭曲面的磁通量等于零，或者，磁场是一个无源场。
- 法拉第感应定律：该定律描述时变磁场怎样感应出电场。电磁感应是制造许多发电机的理论基础。例如，一块旋转的条形磁铁会产生时变磁场，这又接下来会生成电场，使得邻近的闭合电路因而感应出电流。
- 麦克斯韦-安培定律：该定律阐明，磁场可以用两种方法生成：一种是靠传导电流（原本的安培定律），另一种是靠时变电场，或称位移电流（麦克斯韦修正项）。
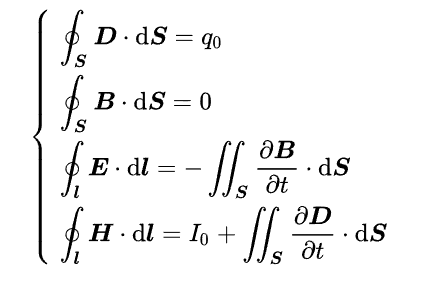
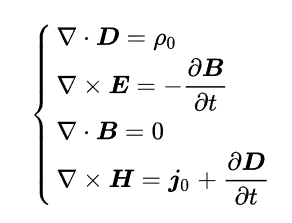
考虑函数f (x)围绕点x0展开的Taylor级数展开式，其偏移量为±δ/2：
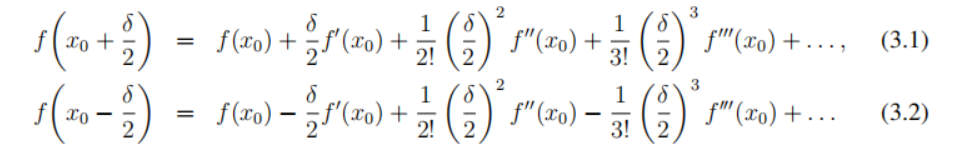
两式相减可得
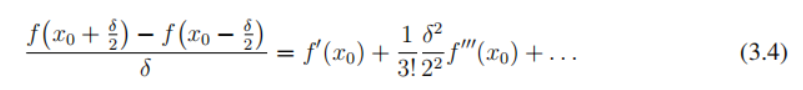
整理一下可以变成
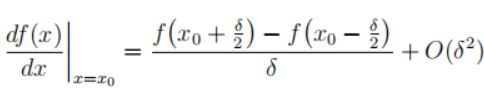
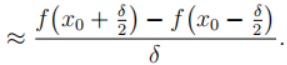左边为关于位移的导数右边为中心差分与高阶无穷小，近似等于中心差分（在极限下，当δ趋于零时，近似就变得精确）
由Kane Yee在1966年首次提出的FDTD算法采用了二阶中心差异。该算法可总结如下：
1.用有限差分代替安培定律和法拉第定律中的所有导数
2.求解得到的差分方程，得到“更新方程”，用（已知的）过去的场来表示（未知的）未来的场。
3.在未来的一个时间步中评估磁场与
4.在未来的一个时间步中评估磁场与
5.重复循环
在一维FDTD中法拉第定律可以写作：
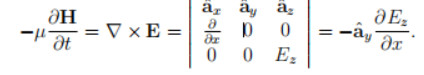变为标量形式为：
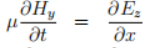根据电场的空间导数给出了磁场的时间导数。
安培定律可以写作：
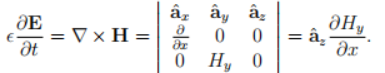变为标量形式为：
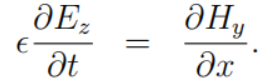根据磁场的空间导数给出了电场的时间导数。
再用有限的差值替换上式中的导数以做到离散化
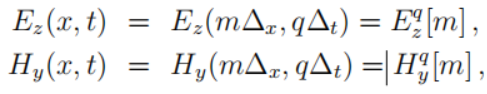m表示空间步，q表示时间步
如下图所示，第一个方程将用于及时推进磁场，而第二个方程将用于推进电场。一种方法，其中一个场是先进的，然后是另一个场，然后重复这个过程，被称为跳蛙法。
更新磁场后
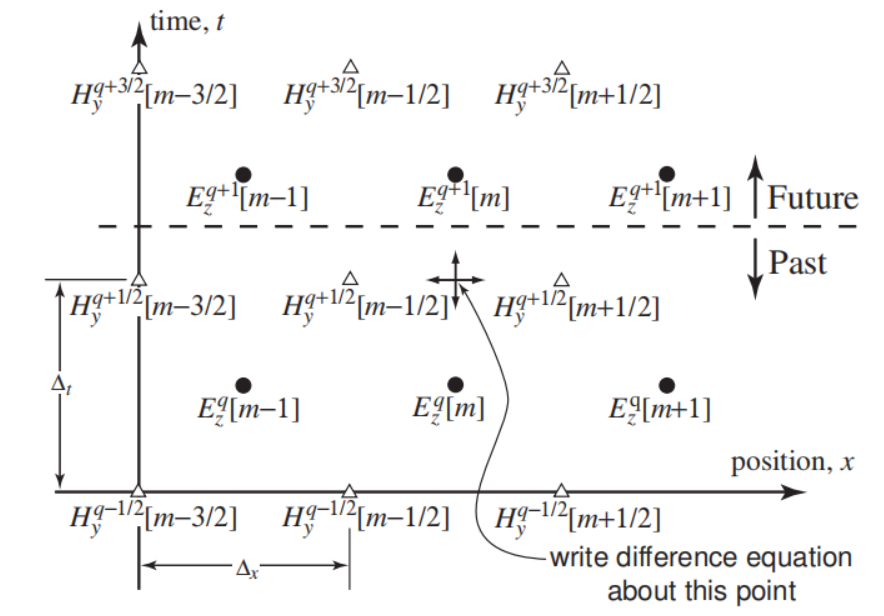
上图更新主要涉及两个差分等式：
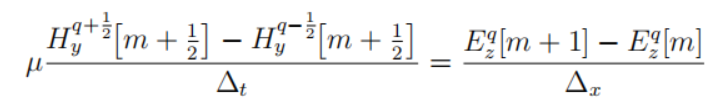整理可得
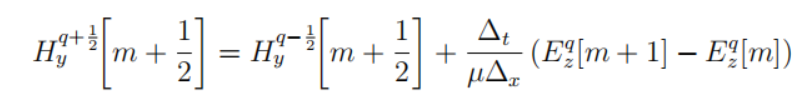代表过去半个时刻的两个相邻位置电场以及过去一个时刻的磁场推导出未来半个时刻的磁场
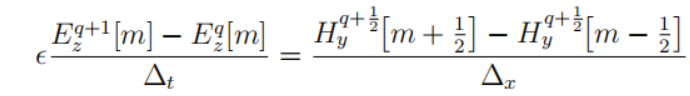整理可得
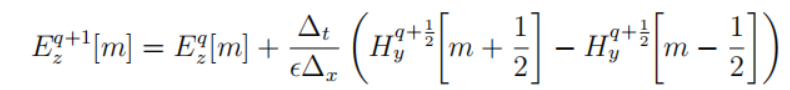代表过去半个时刻的两个相邻位置磁场以及过去一个时刻的电场推导出未来半个时刻的电场
转换成代码就是两句赋值语句（imp0代表自由空间的特征阻抗）：
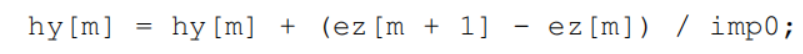
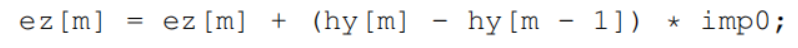
下面为简要代码：
1 /* Bare-bones 1D FDTD simulation with a hard source. */ 2 3 #include <stdio.h> 4 #include <math.h> 5 6 #define SIZE 200 7 8 int main() 9 { 10 double ez[SIZE] = {0.}, hy[SIZE] = {0.}, imp0 = 377.0; 11 int qTime, maxTime = 250, mm; 12 13 /* do time stepping */ 14 for (qTime = 0; qTime < maxTime; qTime++) { 15 16 /* update magnetic field */ 17 for (mm = 0; mm < SIZE - 1; mm++) 18 hy[mm] = hy[mm] + (ez[mm + 1] - ez[mm]) / imp0; 19 20 /* update electric field */ 21 for (mm = 1; mm < SIZE; mm++) 22 ez[mm] = ez[mm] + (hy[mm] - hy[mm - 1]) * imp0; 23 24 /* hardwire a source node */ 25 ez[0] = exp(-(qTime - 30.) * (qTime - 30.) / 100.); 26 27 printf("%g\n", ez[50]); 28 } /* end of time-stepping */ 29 30 return 0; 31 }
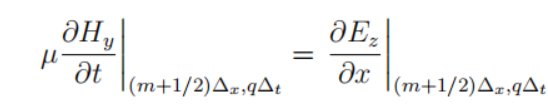
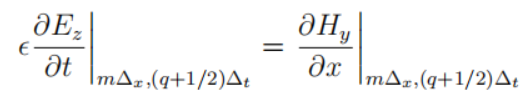
posted on
