第1期 考研中有关函数的一些基本性质《zobol考研微积分学习笔记》

在入门考研微积分中，我们先复习一部分中学学的初等数学的内容。函数是非常有用的数学工具。

1.函数的性质理解：

首先考研数学中的所有函数都是初等函数。而函数的三个关键就是定义域、值域、对应关系f。

其中定义域和值域都必须是实数集，也就是只可以是“数”，并且必须是有理数或无理数。（考研我们不涉及虚数集的映射）。

对应关系f要明确必须是“一对一”或“多对1”，不允许“一对多”

 

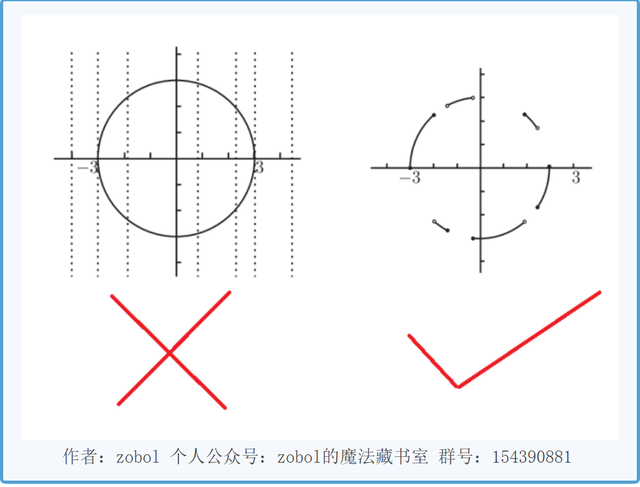
但是如果等式具有对称性，那么我们就可以通过约束定义域、值域，来利用函数研究原本等式的性质（考研给的一般都是圆或者椭圆这类的对称）。

2.函数图像的重要性

考研数学中涉及到的绝大部分函数都可以画出大致的图像，而且解题的思路往往都和图像有关系。

在中学，我们学习过一元二次函数和基本三角函数的图像画法，但是考研微积分中的大部分函数的具体图像在考场上是画不出来的。我们一般都是研究部分定义域内的函数图像的大致走向。

一般都是研究x=0处附近的函数图像，更多的关注，函数的走向（向上还是向下），图像在x轴的上方还是下方，过不过原点，函数图像的拐点。

 

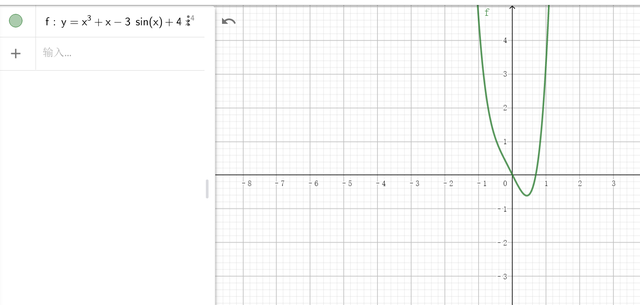
3.如何画出大致的函数图像：

正常采用的是求导求导函数，特殊值代入，已知的其他函数图像类似联想。其中主要还是依靠导函数。