开始讨论离散型随机变量吧！《考研概率论学习之我见》 -by zobol

上一文中，笔者给出了随机变量的基本定义：一个可测映射，从结果空间到实数集，我们的目的是为了引入函数这个数学工具到考研概率论中，但是我们在现实中面对的一些事情结果，映射而成的随机变量和其对应的概率值，并不能映射一个有太多用的函数。这就是离散型随机变量。我们先讨论它，因为离散型随机变量有关的分布都比较简单。如果要学习离散型随机变量，必须要引入可数集的概念。

 

1.为什么要单独提出来离散型随机变量？

2.离散型随机变量的个数可以是无限个吗？

3.先给出"离散"的定义

4.什么是可数集？什么是不可数集？

5.可数和离散的关系？

6.从可数集的角度来定义离散型随机变量

7.从概率质量函数的角度来看离散型随机变量

 

1.为什么要单独提出来离散型随机变量？

这主要是因为我们在考研微积分中学到的所有基本函数，在其单个定义域内都是连续的。所有的数学工具都是基于此的。如果是一个定义域完全离散的函数，它每个点都不可导，求不出极值和导函数，也无法应用牛顿-莱布尼茨积分公式，那其实这个概率函数就在考研范围内没什么讨论价值。

 

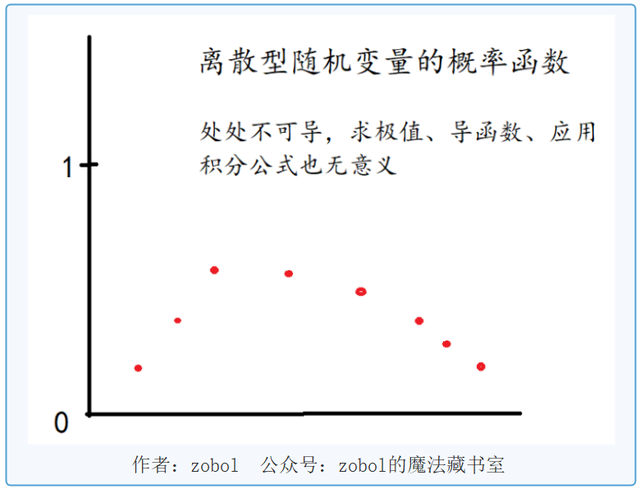
对于这些概率函数所对应的随机变量，我们就单独拿出来叫做离散随机变量，我们也可用一些函数去拟合它们，但就考研来讲，更常用的工具是分布列去研究它们。

 

2.离散型随机变量的个数可以是无限个吗？

可以是无限个，但是是有条件的。严格定义应该是离散型随机变量的实数集必须是有限集或者可数集。通俗理解就是映射集合中任意两个数之间，只能有限个数的。但是本文就不讨论怎么定义两个数紧挨，因为实数集中任意两个数只要不相等，中间就一定有无限个数字。最常见的可数集就是自然数集。

 

3.先给出"离散"的通俗定义

离散的通俗定义，就是任取两个数字，中间只有有限个数字。这是因为在实数集中，任取两个不相等的数字，中间一定有无限个数字。也就是我们常认为那种两个数字之间紧挨的情况实际上是找不到的，所以只要有有限个数字，那么一定无法连续。

 

4.什么是可数集？什么是不可数集？

自然数集是最常见的无穷可数集，实数集是最常见的无穷不可数集。

解释1：可数集还有一个名字就是可列集，就是可排列的数集合，实际是指你在一个集合中任取两个数字，它们中间的数字可以被排列。如果你想排列一组数据，无论是什么排列法则，你都需要遍历一遍，如果两个数字中间有无穷个数字，那你就无法遍历了，也就无法排序。所以可以看做是可数集就是任取两个数字，中间只能有有限个数字。

解释2：可数集就是能与自然数集的某个子集一一对应的集合，就是一定可以和{1、2、3、4.....}构成一个双射，至于无限个还是有限个，到是无所谓。注意自然数集是一个离散型的数集。

 

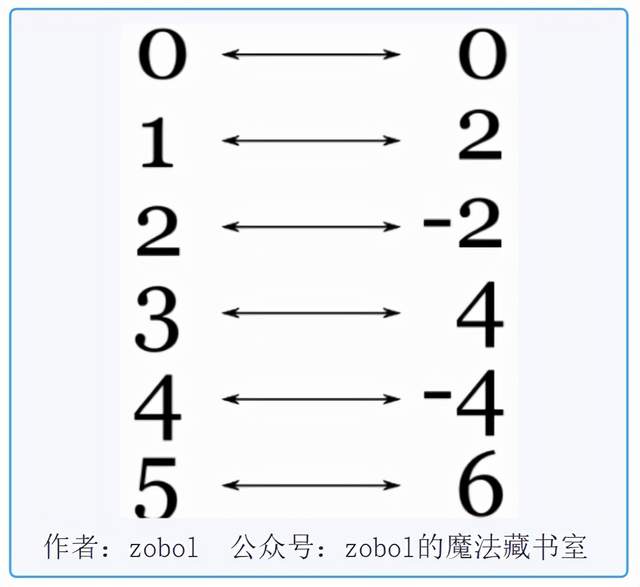
（笔者认为定义2更好理解，书上也是这样定义的）

 

5.可数和离散的关系？

简单来说，可数就代表离散。不可数就代表连续。因为可数集的定义就是能跟自然数集的某个子集形成双射，而自然数集就是离散的。

 

6.从可数集的角度来定义离散型随机变量。

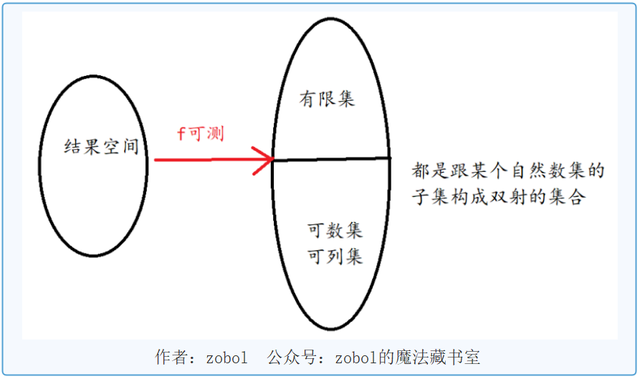
之前我们都是从数集的角度来看，但是我在好多书上，都是从结果空间/样本空间来定义离散型随机变量。

定义：如果一个随机变量的结果空间能跟一个可数集或者有限集构成映射，则认为是离散型随机变量。

（有些书上的定义，有个至多可数集，其实就是可数集-有限集）

 

6.从概率质量函数的角度来看离散型随机变量

有的资料也有从函数角度来看随机变量的。就是指如果一个随机变量对应的概率函数的定义域是离散的，也就是如果这个概率函数是一个离散函数，那就认为是离散型随机变量。不过考研是不研究离散函数的性质的，就不继续讨论了。

 

最后给出离散型随机变量的定义：

***定义1：如果一个随机变量的结果空间能跟自然数集的某个子集构成映射，则认为是离散型随机变量。

定义2：如果一个随机变量的结果空间能跟一个可数集或者有限集构成映射，则认为是离散型随机变量。

定义3：如果一个概率函数是一个离散函数，那其定义域对应的随机变量就是离散型随机变量。