AGC066 题解

题解：AT_agc066_a [AGC066A] Adjacent Difference

笑点解析：没有必要将总成本最小化。

我们将格子间隔的黑白染色（显然有两种染色方法），对于黑点我们要求它是奇数倍 \(d\)，对于白点我们要求它是偶数倍 \(d\)，这样一定满足相邻格子相差至少 \(d\)。

因为两种染色方法的代价和为 \(dN^2\)，所以两种方法中至少有一种满足代价小于 \(\frac{1}{2}dN^2\)，容易实现：

ll n, m, ans = 1e15, Case=1;
ll a[N][N], b[N][N], c[N][N];
void solve() {
	input(n, m);
	for(ll i = 1; i <= n; i++) {
		for(ll j = 1; j <= n; j++) {
			input(a[i][j]);
		}
	}
	for(ll x = 0; x <= 1; x ++) {
		ll sum = 0;
		for(ll i = 1; i <= n; i ++) {
			for(ll j = 1; j <= n; j ++) {
				ll k = a[i][j] / m;
				if((i + j + k + x) % 2 == 0) {
					if(a[i][j] < 0) k --;
					else k ++;
				}
				b[i][j] = k * m;
				sum += abs(b[i][j] - a[i][j]);
			}
		}
		if(sum < ans) {
			for(ll i = 1; i <= n; i ++) {
				for(ll j = 1; j <= n; j ++) {
					c[i][j] = b[i][j];
				}
			}
			ans = sum;
		}
	}
	for(ll i = 1; i <= n; i ++) {
		for(ll j = 1; j <= n; j ++) {
			print(c[i][j]);
		}
		putchar('\n');
	}
//	print(ans);
}

题解：AT_agc066_b [AGC066B] Decreasing Digit Sums

题目大意：给定 \(n\)，求一个 \(x\)，使得对于任意的 \(1\le i\le n\)，满足 \(d(2^{i-1}x)>d(2^ix)\)。其中 \(d(x)\) 指 \(x\) 的数位和。

我们发现，答案是具有单调性的，也就是对于 \(n=50\) 的答案，同样适用于 \(n<50\) 的情况。

所以我们只用考虑 \(n=50\) 的答案即可。

按照直观的感受，给定任意的 \(x\) 与 \(y\)，已知 \(x>y\)，那么 \(d(x)\) 大于 \(d(y)\) 的概率会比较大。

但是随着 \(i\) 的增加，\(2^ix\) 也会随之增加，所以我们要考虑减小 \(d(2^ix)\)。

我们发现，如果某一个数位为 \(0\)，对于 \(d\) 函数就没有贡献。所以考虑构造一个 \(x\)，使得它乘上 \(2^i\) 可以产生若干个 \(0\)。所以设 \(x=5^{50}a\)，那么 \(d(2^ix)=d(2^i5^{50}a)=d(10^i5^{50-i}a)=d(5^{50-i}a)\)，此时随着 \(i\) 的增加，\(5^{50-i}a\) 也会随之减小，那么 \(d(5^{50-i}a)\) 肯定也会趋于减小。具体：

但是这样仍旧不是单调递减的，但是它是趋于单调递减的，所以我们可以考虑把它们拼接起来，这样平均下来，单调递减的概率就会大大上升。

我们随机得到 \(a_1,a_2,\cdots,a_k\)，然后将这 \(k\) 个系数组成的数用 \(0\) 连接起来，这样就可以保证它单调递减的概率比较大：

下面代码中的 bign 是高精度，check 是判断是否合法的函数：

ll n = 50, k = 100;
bign a = 1, ans;
int main() {
	for(ll i = 1; i <= 50; i ++) a = a * 5;
	while(true) {
		ans = 0;
		for(ll i = 1; i <= k; i ++) {
			ll x = rnd() % 100 + 1;
			bign tmp = a * x;
			for(ll j = 1; j <= tmp.len + 50; j ++) ans = ans * 10;
			ans = ans + tmp;
		}
		if(check(ans)) {
			cout << ans << endl;
			break;
		}
	}
	return 0;
}

一种可能的结果

题解：AT_agc066_c [AGC066C] Delete AAB or BAA

这题评黑我觉得有点过了。其实还是比较好想的。

考虑一个区间怎么才能被消除掉：它满足可以分成若干个满足以下条件的子串：每个子串都满足 \(\tt A\) 的数量是 \(\tt B\) 的两倍，左端点或右端点是 \(\tt B\)。

证明可以让时间倒流，我们在这个字符串内不断添加 \(\tt AAB\) 或 \(\tt BAA\)。

如果一个字符串是空字符串，添加 \(\tt AAB\) 或 \(\tt BAA\) 明显符合。

如果一个字符串符合条件，那么在两端添加 \(\tt AAB\) 或 \(\tt BAA\) 相当于添加了一个新的符合条件的子串，如果在中间添加 \(\tt AAB\) 或 \(\tt BAA\)，字符串两端的字符仍旧不变，依旧符合。

所以通过归纳法可以证明。

所以我们设 \(x_i\) 表示 \(1\sim i\) 中 \(\tt B\) 的数量的两倍减去 \(\tt A\) 的数量。若 \(x_l=x_r\)，则 \([l+1,r]\) 明显是一个可以被消除掉的字符串。

所以我们容易设 \(f_i\) 表示处理到第 \(i\) 个字符，最少不删掉的字符的数量，明显我们需要最小化它。

那么有转移方程：

\[f_i=\begin{cases} f_{i-1}+1 \\ f_j & x_i=x_j,s_{j+1}={\tt B} \\ f_j & x_i=x_j,s_{i}={\tt B} \end{cases} \]

对于第二、三种情况，我们可以用两个 map 来储存每种 \(x\) 下的最小 \(f\) 值。

这里不使用 \(f_i\) 表示最多不删除的字符数量的原因是因为不太好打。

void solve() {
	map<ll, ll> ha, hb;
	scanf("%s", s + 1);
	n = strlen(s + 1);
	for(ll i = 1; i <= n; i ++) {
		a[i] = a[i - 1], b[i] = b[i - 1];
		if(s[i] == 'A') {
			a[i] ++;
		}
		else {
			b[i] ++;
		}
		x[i] = a[i] - 2 * b[i];
		ha[x[i]] = hb[x[i]] = inf;
	}
	ha[0] = hb[0] = inf;
	for(ll i = 1; i <= n; i ++) {
		f[i] = inf;
	}
	if(s[1] == 'A') {
		ha[0] = 0;
	} else {
		hb[0] = 0;
	}
	for(ll i = 1; i <= n; i ++) {
		f[i] = min(f[i], f[i - 1] + 1);
		if(s[i] == 'A') {
			f[i] = min(f[i], hb[x[i]]);
		} else {
			f[i] = min(f[i], ha[x[i]]);
			f[i] = min(f[i], hb[x[i]]);
		}
		if(s[i + 1] == 'A') {
			ha[x[i]] = min(ha[x[i]], f[i]);
		} else {
			hb[x[i]] = min(hb[x[i]], f[i]);
		}
	}
	print((n - f[n]) / 3);
	putchar('\n');
}

题解：AT_agc066_e [AGC066E] Sliding Puzzle On Tree

笑点解析：P6277。

发现交换操作有可传递性：如果 \((x,y)\) 两个位置（注意我们这里是位置而不是指石子）可以互相交换，\((y,z)\) 两个位置也可以互相交换，那么 \((x,z)\) 两个位置必定是可以互相交换的。因为可以先交换 \((x,y)\)，再交换 \((y,z)\)，最后再次交换 \((x,y)\)。

我们发现如果当前如果有 \(k\) 个石子，无论它们在哪些位置，我们总是可以移动它们到树上的 \(1\cdots k\) 号位置。也就是说，如果忽略标号的话，任意两个状态都是直达的。

所以我们固定这 \(k\) 个石子在 \(1\cdots k\) 号位置，计算有多少种有标号的排列状态。

假如 \((x,y)\) 两个石子能够在不影响其它石子的情况下交换，我们就给它们连一条边，发现最后面会形成很多个团（完全图）。根据交换操作的可传递性，那么每一个团的情况肯定是可以互相到达的。

我们设这些团大小为 \(s_i\)，那么答案就是 \(\binom{n}{k}\times\prod (s_i!)\)。

考虑怎样的情况下两个石子是可以交换的：

首先，我们可以把石子从位置 \(1\cdots k\) 移出来到任意位置。

然后在不影响其它石子的情况下交换两个石子。

最后，按照相反的顺序移动回位置 \(1\cdots k\)。

此时，两个石子就是可交换的，连一条边。

考虑怎样在不影响其它石子的情况下交换两个石子：

发现当在一条没有石子的链且出现一个分支时，两个石子可以交换：

如上，位置 \(1\) 上的石子和位置 \(6\) 上的石子交换时，可以在这个没有石子且有一个分支 \(4\) 的链 \(2\to5\) 上进行交换。先把 \(1\) 上的石子移动到 \(4\) 上，再把 \(6\) 上的石子移动到 \(1\) 上，最后把移动到 \(4\) 上的石子移动到 \(6\) 上。

总结可以交换的规律：

  1. 没有石子的链；
  2. 有一个分支（有一个位置度数大于二）。

我们将其拓展一下：

在一个中间都是二度点，两端都是非二度点的链上，设两端不包括链的树的大小分别为 \(a\)、\(b\)，链的长度为 \(c\)（它们都包括两端的点）：

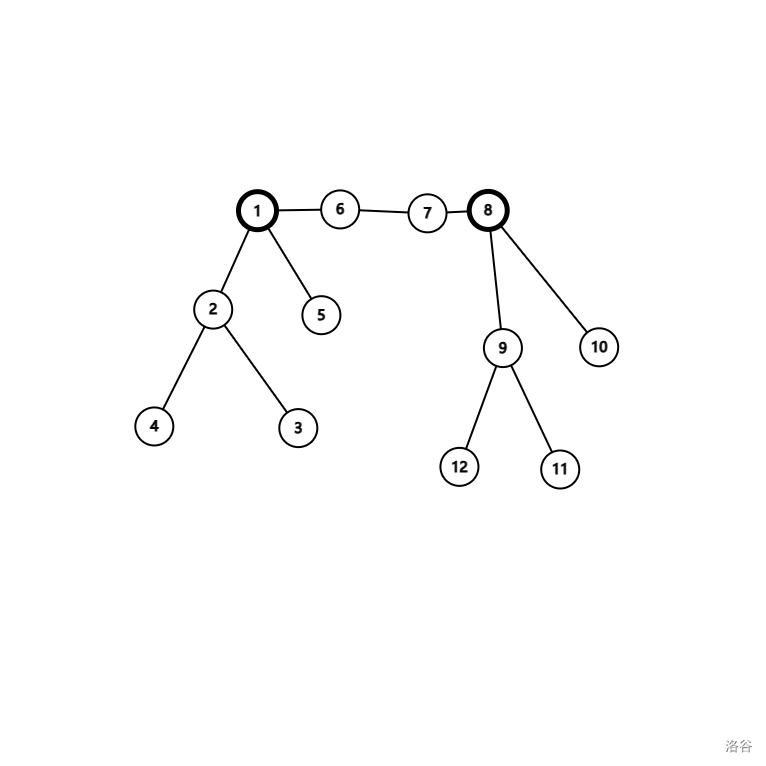
如上，\(1\to8\) 就是合法的中间都是二度点，两端都是非二度点的链。其中 \(a=5\)（位置 \(1\)，\(2\)，\(3\)，\(4\)，\(5\) 都是左端的树），\(b=5\)（位置 \(8\)，\(9\)，\(10\)，\(11\)，\(12\) 都是右端的树），\(c=4\)（位置 \(1\)，\(6\)，\(7\)，\(8\) 都是中间的链）。

我们发现，当 \(k\le(a-1)+(b-1)-1\) 时，两端的树上的每一个位置都可以互相交换，也就是能到达左端的石子和能到达右端的石子一定可以交换，我们对这两个石子连边。

原理：将 \(k\) 个石子任意的移动到两颗树上，留下一个空位置作为交换的分支，然后树上的任意两个石子都可以通过这个分支和没有石子的链进行交换。

总结可以交换的规律：\(k<(a-1)+(b-1)\)，也就是 \(k<n-c\)。

发现，若 \((x,y)\) 是满足这个条件的一条链，也就是能到达 \(x\) 的石子能和能到达 \(y\) 的石子交换。以及若 \((y,z)\) 也是满足这个条件的一条链，那么能到达 \(x\) 的石子能肯定也能和能到达 \(z\) 的石子交换。

也就是说，我们链的两端可以互相连接形成很多个连通块

我们可以把每个满足交换条件，也就是 \(k<n-c\) 的链的两端连接起来，因为可以到达这两个位置的石子就可以和能到达另一个位置的石子交换，所以说，我们计算能到达这些点的石子的个数，即可得到 \(s_i\)，也就是团的大小。

因为当 \(k\) 从小到大枚举时，\(k<n-c\) 也就是 \(c<n-k\) 的边是越来越少的，不好维护。考虑时光倒流，将 \(k\) 从大到小枚举时，\(c<n-k\) 的边将会越来越多，用并查集即可维护。

回到刚刚那个问题，怎么计算能到达这些点的石子的个数？

正難则反，我们可以计算出无法到达这个连通块的石子的个数，再用石子的总数 \(k\) 减去即可。

如果 \(a_i\to b_i\) 不是一条满足上面交换条件的链，设连通块外的树的大小为 \(a_i\)，连通块内树的大小为 \(b_i\)，链的长度为 \(c_i\)。

那么我们能够进入到这个联通块的最多只有 \(b_i-1\) 个石子，也就是把连通块内树全部填满，那么还有 \(k-(b_i-1)\) 的石子无法与之交换。

那么总共的可到达的节点数量为：

\[\begin{aligned} k-\sum_{a_i\to b_i}(k-(b_i-1)) &= k-\sum_{a_i\to b_i}(k-(n-a_i-(c_i-1))) \\ &= k-\sum_{a_i\to b_i}(k-n+a_i+c_i-1) \\ \end{aligned} \]

发现 \(a_i+c_i-1\) 为“联通块内子树” 外的点减一（\(c_i\) 有一端在连通块内），所以设 \(p_i\) 为链方向连通块外的点的个数，有：

\[\begin{aligned} k-\sum_{a_i\to b_i}(k-(b_i-1)) &= k-\sum_{a_i\to b_i}(k-n+p_i+1) \\ &= k-(\sum_{a_i\to b_i}(k-n+1)+\sum_{a_i\to b_i}p_i) \end{aligned} \]

设连通块大小为 \(\text{siz}\)，不合法的 \(a_i\to b_i\) 个数为 \(\text{out}\)。我们发现子树外的点数和 \(\sum_{a_i\to b_i}p_i=n-\text{siz}\)。有：

\[\begin{aligned} k-\sum_{a_i\to b_i}(k-(b_i-1)) &= k-([\text{out}](k-n+1)+n-[\text{siz}]) \\ &= k-[\text{out}](k-n+1)-n+[\text{siz}] \\ &= ([\text{out}]-1)(n-k-1)+[\text{siz}]-1 \end{aligned} \]

我们维护一下连通块的 \(\text{out}\) 和 \(\text{siz}\) 即可。注意在合并的时候，双方的 \(\text{out}\) 和 \(\text{siz}\) 都会减小！

因为每一次连通块个数等于不合法链的数量加上一，而不合法链只能存活链长的时间，所以均摊之后是 \(O(n)\) 的。连通块使用 set 维护。所以时间复杂度为 \(O(n\log n)\)。精细实现能够做到更优。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define N 200010
#define P 998244353
ll t, n;
ll deg[N];
ll head[N], nxt[2 * N], to[2 * N], cnt;
ll fa[N], out[N], siz[N];
ll ans[N], fac[N], ifac[N];
set<ll> s;
struct node {
	ll a, b, c;
	node(ll a = 0, ll b = 0, ll c = 0):a(a), b(b), c(c) {}
} edge[N];
ll tot;
void addEdge(ll u, ll v) {
	cnt ++;
	to[cnt] = v;
	nxt[cnt] = head[u];
	head[u] = cnt;
}
ll find(ll x) {
	if(fa[x] == x) {
		return x;
	}
	return fa[x] = find(fa[x]);
}
void merge(ll a, ll b, ll c) {
	a = find(a), b = find(b);
	fa[a] = b;
	siz[b] += siz[a] + c - 2;
	out[b] += out[a] - 2;
	s.erase(a);
}
void dfs(ll u, ll fa, ll rt, ll c) {
	if(deg[u] != 2) {
		if(rt) {
			edge[++ tot] = node(u, rt, c);
		}
		c = 1;
		rt = u;
	}
	for(ll i = head[u]; i; i = nxt[i]) {
		ll v = to[i];
		if(v == fa) continue;
		dfs(v, u, rt, c + 1);
	}
}
ll qpow(ll x, ll y) {
	if(y == 0) return 1;
	if(y % 2 == 1) return x * qpow(x, y - 1) % P;
	ll tmp = qpow(x, y / 2);
	return tmp * tmp % P;
}
int main() {
	scanf("%lld", &t);
	while(t --) {
		scanf("%lld", &n);
		
		for(ll i = 1; i <= n; i ++) {
			head[i] = 0, deg[i] = 0, fa[i] = 0, siz[i] = 0, out[i] = 0;
		}
		cnt = 0, tot = 0;
		s.clear();
		
		for(ll k = 1; k < n; k ++) {
			ll u, v;
			scanf("%lld %lld", &u, &v);
			addEdge(u, v);
			addEdge(v, u);
			deg[u] ++;
			deg[v] ++;
		}
		for(ll i = 1; i <= n; i ++) {
			if(deg[i] != 2) {
				fa[i] = i;
				siz[i] = 1;
				out[i] = deg[i];
				s.insert(i);
			}
		}
		dfs(*s.begin(), 0, 0, 0);
		sort(edge + 1, edge + 1 + tot, [&](const auto &x, const auto &y) {
			if(x.c == y.c) {
				if(x.a == y.a) return x.b < y.b;
				else return x.a < y.a;
			}
			return x.c < y.c;
		});
		fac[0] = 1;
		for(ll i = 1; i <= n; i ++) {
			fac[i] = fac[i - 1] * i % P;
		}
		ifac[n] = qpow(fac[n], P - 2);
		for(ll i = n; i >= 1; i --) {
			ifac[i - 1] = ifac[i] * i % P;
		}
		ans[n] = 1;
		ll pos = 1;
		for(ll k = n - 1; k >= 1; k --) {
			while(pos <= tot && k < n - edge[pos].c) {
				merge(edge[pos].a, edge[pos].b, edge[pos].c);
				pos ++;
			}
			ans[k] = fac[n] * ifac[k] % P * ifac[n - k] % P;
			for(ll i : s) {
				(ans[k] *= fac[(out[i] - 1) * (n - k - 1) + siz[i] - 1]) %= P;
			}
		}
		for(ll i = 1; i <= n; i ++) {
			printf("%lld ", ans[i]);
		}
		printf("\n");
	}
}
posted @   ZnPdCo  阅读(90)  评论(0)  编辑  收藏  举报
相关博文：
·  算法中的变形金刚——单纯形算法学习笔记
·  2024-01-11 训练总结
·  AGC001 ~ 010
·  AGC066 题解
·  AGC 做题合集 #5
阅读排行：
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型，支持深度思考和联网搜索！
· 使用C#创建一个MCP客户端
· ollama系列1：轻松3步本地部署deepseek，普通电脑可用
· 基于 Docker 搭建 FRP 内网穿透开源项目（很简单哒）
· 按钮权限的设计及实现
点击右上角即可分享
微信分享提示
SQL AI 助手