6980. 【2021.02.03冬令营模拟】你的世界(world) Another Solution
Problem Description
Input
从文件
world.in中读入数据。
Output
输出到文件
world.out中。输出共 T 行,第 i 行表示第 i 组测试数据的答案,如果可行则输出 Yes,否则输出 No。
Sample Input Copy
样例输入1: 1 2 3 000 000 111 001 样例输入2: 1 3 4 0000 0101 0001 1011 0001 1100 样例输入3: 1 4 5 11000 01010 00011 10110 00011 11001 11010 10001 Sample Output Copy
样例输出1: Yes 样例输出2: Yes 样例输出3: No Data Constraint
首先,\(A\gets A\oplus B\),我们的问题就变成了怎么操作使得一个空矩阵变成新的矩阵 \(A\)。
先考虑只能操作行和列,该怎么做。
如果这张图是合法的,我们发现对于任意的 \(2\times2\) 子矩阵 \(\begin{bmatrix} a_{0,0} & a_{0,1} \\ a_{1,0} & a_{1,1} \end{bmatrix}\),有 \(a_{0,0}\oplus a_{0,1}\oplus a_{1,0}\oplus a_{1,1}=0\)。
我们来证明一下,因为对于操作行和列,一定会操作 \(2\times2\) 子矩阵中的任意两个,那么异或结果不变。
所以,我们定义 \(a_{0,0},a_{0,1},a_{1,0},a_{1,1}\) 这类异或结果不变的为固定元素,其余的为不固定元素。
\(2\times2\) 子矩阵中有固定元素,也就是这个子矩阵被固定了,所以它合法。
存不存在更小的子矩阵呢?比如说 \(1\times1\) 子矩阵。
答案是不存在的,因为对于一个 \(1\times1\) 子矩阵 \(\begin{bmatrix} a_{0,0} \end{bmatrix}\),我们可以随意修改这个点,所以不存在固定元素,不合法。
考虑加入对角线操作。
如果还是刚刚的 \(2\times2\) 矩阵,我们发现由于对角线操作的加入可以出现形如 \(\begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix}\),\(\begin{bmatrix} 0 & 0 \\ 0 & 1 \end{bmatrix}\) 等等等等的矩阵,子矩阵中没有一个元素是固定元素,这个子矩阵是不固定的!
所以考虑更大的子矩阵。
考虑一个 \(4\times4\) 子矩阵,我们发现对于任意的 \(4\times4\) 子矩阵 \(\begin{bmatrix} a_{0,0} & \textcolor{red}{a_{0,1}} & \textcolor{red}{a_{0,2}} & a_{0,3} \\ \textcolor{red}{a_{1,0}} & a_{1,1} & a_{1,2} & \textcolor{red}{a_{1,3}} \\ \textcolor{red}{a_{2,0}} & a_{2,1} & a_{2,2} & \textcolor{red}{a_{2,3}} \\ a_{3,0} & \textcolor{red}{a_{3,1}} & \textcolor{red}{a_{3,2}} & a_{3,3} \\ \end{bmatrix}\),有 \(a_{0,1}\oplus a_{0,2}\oplus a_{1,0}\oplus a_{1,3}\oplus a_{2,0}\oplus a_{2,3}\oplus a_{3,1}\oplus a_{3,2}=0\)。(为了方便我将这些固定元素标红)
证明显然:
- 对于 \(a_{0,0},a_{0,3},a_{3,0},a_{3,3}\),可以进行一个对角线操作,所以这些元素是可以随便调整的,是不固定元素;
- 对于 \(a_{0,1},a_{0,2},a_{1,0},a_{1,3},a_{2,0},a_{2,3},a_{3,1},a_{3,2}\),这些元素无法抵消,只能进行对角线同时操作两个固定元素,所以异或结果不会变化;
- 对于 \(a_{1,1},a_{1,2},a_{2,2},a_{2,2}\),这些元素可以通过乱搞抵消,具体自己乱搞。
所以这个子矩阵是固定的。
我们继续发现,不存在比 \(4\times4\) 还小的子矩阵。
所以这道题就很简单了,枚举矩阵 \(A\) 的子矩阵左上角 \((i,j)\),只需要所有的子矩阵均满足满足 \(a_{i,j+1}\oplus a_{i,j+2}\oplus a_{i+1,j}\oplus a_{i+1,j+3}\oplus a_{i+2,j}\oplus a_{i+2,j+3}\oplus a_{i+3,1}\oplus a_{j+3,2}=0\),则这张图有解。
时间复杂度 \(O(nm)\)。
然后这道题就可以开始加强了,比如加入各种新印章,都可以用这种方法轻松解决。
#include <cstdio> #include <chrono> #include <random> using namespace std; using namespace chrono; #define ll long long #define N 1010 ll t, n, m; char a[N][N], b[N][N]; int main() { freopen("world.in", "r", stdin); freopen("world.out", "w", stdout); scanf("%lld", &t); while(t--) { scanf("%lld %lld", &n, &m); for(ll i = 1; i <= n; i++) { scanf("%s", a[i]+1); } for(ll i = 1; i <= n; i++) { scanf("%s", b[i]+1); for(ll j = 1; j <= m; j++) { if(a[i][j] == b[i][j]) a[i][j] = 0; else a[i][j] = 1; } } bool flag = 1; for(ll i = 1; i <= n - 3; i++) { for(ll j = 1; j <= m - 3; j++) { if(a[i][j+1] ^ a[i][j+2] ^ a[i+1][j] ^ a[i+1][j+3] ^ a[i+2][j] ^ a[i+2][j+3] ^ a[i+3][j+1] ^ a[i+3][j+2]) { printf("No\n"); flag = 0; break; } } if(!flag) break; } if(flag) printf("Yes\n"); } }



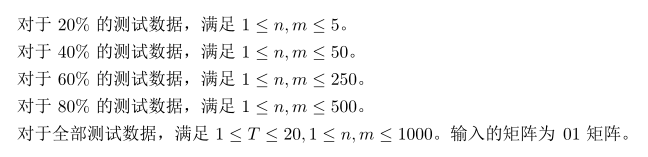


· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 按钮权限的设计及实现