NOI 2024省选OIFC模拟21 蒲巴巴 超繁做法
题目描述
一年一度的 PuBaBa 杯开始了！
今年的 PuBaBa 杯总共有 \(n\) 个选手来参加，编号分别为 \(1,2,\cdots,n\)，他们的水平按编号依次递增，所以他们过的题目数量单调不降。
作为本场比赛的出题人，PuBaBa 总共出了 \(m\) 道题，他希望第 \(i\) 道题至少有 \(l_i\) 个选手通过，至多有 \(r_i\) 个选手通过，PuBaBa 预计所有题的过题人数和为 \(S\)。
作为毒瘤出题人，PuBaBa 例行会在赛前举行“毒奶”活动。不过，PuBaBa 的毒奶是有依据的，他会计算每位选手最多过的题目数量。
不过，PuBaBa 有点太牛了，他决定将这个简单的任务交给您来完成。
输入格式
第一个，三个正整数 \(n,m,S\) 分别表示参赛选手，题目数量，以及总过题人数。
接下来 \(m\) 行，每行两个正整数 \(l_i,r_i\) 表示第 \(i\) 道题至少有 \(l_i\) 个选手通过，至多有 \(r_i\) 个选手通过。
输出格式
若无解，输出 "-1"（不包含双引号）。
否则，为了压缩输出量，我们令 \(ans_i\) 表示第 \(i\) 个选手的最多过题数。
您仅需输出 \(\bigoplus_{i=1}^{n} ans_ii\)。
样例
Input 1
3 5 8 1 3 2 3 1 3 2 3 1 3Output 1
5Input 2
10 8 41 1 7 5 6 5 7 4 9 7 10 1 2 3 10 3 5Output 2
50样例解释
对于样例一：\(ans\) 序列为 \(2,4,5\)。
对于样例二：\(ans\) 序列为 \(4,4,5,5,6,7,7,7,8,8\)。
数据范围
由于输入量很大，请使用快速的读入方式。
出题人为您准备了一份 fread 板子：https://www.luogu.com.cn/paste/xc3a5u5w。
测试点编号 \(n,m\le\) 特殊性质 \(1\sim 2\) \(5\) 无 \(3\) \(100\) 保证 \(l_i=r_i\) \(4\sim 5\) \(100\) 无 \(6\sim8\) \(1000\) 保证 \(l_i=r_i\) \(9\sim 10\) \(1000\) 无 \(11\sim12\) \(2\times 10^5\) 保证 \(l_i=r_i\) \(13\sim14\) \(10^5\) 无 \(15\sim16\) \(2\times 10^5\) 无 \(17\sim18\) \(5\times 10^5\) 无 \(19\) \(2\times10^6\) 无 \(20\) \(5\times10^6\) 无 对于 \(100\%\) 的数据，保证 \(1\le n,m \le 5\times 10^6\)，\(1\le l_i\le r_i\le n\)，\(1\le S\le nm\)。
比某些做法难，总之比题解简单
先问一个问题：一个长度为 \(n\) 的数组 \(a=\{0\}\)，进行 \(m\) 次操作，每次操作选择若干个互不相同的位置使这些位置加 \(1\)。给你一个数组 \(b\)，问这个数组可否通过上述 \(m\) 次操作得出来。
这题非常简单，我们只需要求出 \(\max_b\)，若 \(\max_b\le m\) 则可以，否则不可以。
我们将原问题化为一个二维问题，横方向表示题目，纵方向表示这道题做出的人数，黄色矩形表示 \([l_i,r_i]\)。
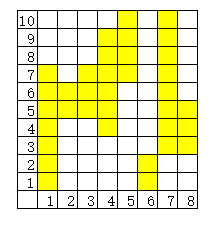
明显得出，我们至少要填 \(\sum l_i\) 个格子，至多能填 \(\sum r_i\) 个格子。如果 \(\sum l_i\le S\le\sum r_i\) 不满足，则答案为 \(-1\)。
我们设考虑到第 \(i\) 个人，则后面有 \(p=n-i+1\) 个人。又设 \(ans_i=j\)。
考虑写一个 check，传入 \(p,j\)，判断是否存在方案。
首先，有一个基础的构造，即必须在这个构造上动工。我们设第 \(i\) 个人的做题数为 \(a_i\)。
明显，这是一个满足递增且第 \(i\) 个人为 \(j\) 的方案。它总共填了 \(p\times j\) 个格子。
先考虑后面 \(p\) 个人的部分。
我们发现，“做题”的操作就很像上面“加一”的操作——选择若干个互不相同的位置使这些位置加 \(1\)。因为有 \(p\) 个人，所以我们就有 \(p\) 次操作。同理，只有每道题过题人数都小于 \(p\) 才合法。（重申一下，先考虑后面 \(p\) 个人的部分）
也就是说，我们需要画一条粗线，只能取粗线下面的部分。（下面这张图举了 \(p=6\) 的例子）
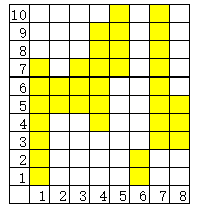
我们发现，对于 \(l_i\le p\)，是合法的，我们可以在后面的部分将其填完，不会超过 \(p\)。至少要填的格子数是 \(\sum l_i[l_i\le p]\)。
但对于 \(l_i>p\)，我们只能填 \(p\) 个。只能填的格子数是 \(\sum p[l_i>p]\)。
我们可以发现，因为存在 \(l_i>p\)，只能填 \(p\) 个的情况。我们需要在前面 \(n-p\) 个人补全这 \(\sum (l_i-p)[l_i>p]\) 个格子，那么现在每个题都满足下边界 \(l_i\) 了。
那么前面的 \(n-p\) 个人有没有足够的位置补全呢？
答案是有的！
设 \(x=\sum [l_i>p]\)，说明 \(a_{n-p+1}\) 至少为 \(x\)，最多有 \((n-p)x\) 个格子需要补全。
前面的 \(a_i\) 必须小于等于 \(x\)，那么最多有 \((n-p)x\) 个位置，恰好可以补全！
我们发现，题目要求我们填恰好 \(S\) 个，我们不一定能填够。由于至少填 \(\sum l_i\) 个，我们有 \(S-\sum l_i\) 个“自由”的格子。
考虑将这些填给后面 \(l_i\le p\) 的题目，努力补全让它们尽量等于 \(p\)。那么总共有 \((S-\sum l_i)+(\sum l_i[l_i\le p])+(\sum p[l_i>p])\) 个格子。将其与至少的格子数 \(pj\) 做比较即可。
完了吗？当然没有。我们是不是忘了某个叫 \(r\) 的东西？
因为我们刚刚进行补全，有可能会补到 \(r\) 之外。我们要与至多的进行比较。
我们求出至多的格子数，同上为：\((\sum r_i[r_i\le p])+(\sum p[r_i>p])\)，与刚刚的总共值取 \(\min\)。
也就是得到了 check 函数。
然后发现答案肯定是递增的。
所以可以均摊线性得到答案。
#include <cstdio>
#include <algorithm>
#include <cctype>
using namespace std;
#define ll long long
#define N 5000010
ll n, m, s, mx, mn, ans[N], ANS;
ll l[N], r[N], sl[N], sr[N], cl[N], cr[N];
int main() {
// freopen("pubaba.in", "r", stdin);
// freopen("pubaba.out", "w", stdout);
scanf("%lld %lld %lld", &n, &m, &s);
for(ll i = 1; i <= m; i++) {
scanf("%lld %lld", &l[i], &r[i]);
mn += l[i], mx += r[i];
sl[l[i]] += l[i];
sr[r[i]] += r[i];
cl[l[i]] ++;
cr[r[i]] ++;
}
if(mn > s || mx < s) return printf("-1"), 0;
for(ll i = 1; i <= n; i++) {
sl[i] += sl[i-1];
sr[i] += sr[i-1];
}
for(ll i = n; i >= 1; i--) {
cl[i] += cl[i+1];
cr[i] += cr[i+1];
}
ll pos = n;
for(ll i = 1; i <= m; i++) {
while(min(s - mn + sl[pos - 1] + pos * cl[pos], sr[pos - 1] + pos * cr[pos]) < pos * i)
pos--;
ans[n - pos + 1] = i;
}
for(ll i = 1; i <= n; i++) {
ans[i] = max(ans[i-1], ans[i]);
ANS ^= ans[i] * i;
}
printf("%lld", ANS);
}
