2024-01-11 训练总结

T1 愤怒的小鸟

[NOIP2016 提高组] 愤怒的小鸟

题目背景

NOIP2016 提高组 D2T3

题目描述

Kiana 最近沉迷于一款神奇的游戏无法自拔。

简单来说，这款游戏是在一个平面上进行的。

有一架弹弓位于 \((0,0)\) 处，每次 Kiana 可以用它向第一象限发射一只红色的小鸟，小鸟们的飞行轨迹均为形如 \(y=ax^2+bx\) 的曲线，其中 \(a,b\) 是 Kiana 指定的参数，且必须满足 \(a < 0\)，\(a,b\) 都是实数。

当小鸟落回地面（即 \(x\) 轴）时，它就会瞬间消失。

在游戏的某个关卡里，平面的第一象限中有 \(n\) 只绿色的小猪，其中第 \(i\) 只小猪所在的坐标为 \(\left(x_i,y_i \right)\)。

如果某只小鸟的飞行轨迹经过了 \(\left( x_i, y_i \right)\)，那么第 \(i\) 只小猪就会被消灭掉，同时小鸟将会沿着原先的轨迹继续飞行；

如果一只小鸟的飞行轨迹没有经过 \(\left( x_i, y_i \right)\)，那么这只小鸟飞行的全过程就不会对第 \(i\) 只小猪产生任何影响。

例如，若两只小猪分别位于 \((1,3)\) 和 \((3,3)\)，Kiana 可以选择发射一只飞行轨迹为 \(y=-x^2+4x\) 的小鸟，这样两只小猪就会被这只小鸟一起消灭。

而这个游戏的目的，就是通过发射小鸟消灭所有的小猪。

这款神奇游戏的每个关卡对 Kiana 来说都很难，所以 Kiana 还输入了一些神秘的指令，使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。

假设这款游戏一共有 \(T\) 个关卡，现在 Kiana 想知道，对于每一个关卡，至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算，所以希望由你告诉她。

输入格式

第一行包含一个正整数 \(T\)，表示游戏的关卡总数。

下面依次输入这 \(T\) 个关卡的信息。每个关卡第一行包含两个非负整数 \(n,m\)，分别表示该关卡中的小猪数量和 Kiana 输入的神秘指令类型。接下来的 \(n\) 行中，第 \(i\) 行包含两个正实数 \(x_i,y_i\)，表示第 \(i\) 只小猪坐标为 \((x_i,y_i)\)。数据保证同一个关卡中不存在两只坐标完全相同的小猪。

如果 \(m=0\)，表示 Kiana 输入了一个没有任何作用的指令。

如果 \(m=1\)，则这个关卡将会满足：至多用 \(\lceil n/3 + 1 \rceil\) 只小鸟即可消灭所有小猪。

如果 \(m=2\)，则这个关卡将会满足：一定存在一种最优解，其中有一只小鸟消灭了至少 \(\lfloor n/3 \rfloor\) 只小猪。

保证 \(1\leq n \leq 18\)，\(0\leq m \leq 2\)，\(0 < x_i,y_i < 10\)，输入中的实数均保留到小数点后两位。

上文中，符号 \(\lceil c \rceil\) 和 \(\lfloor c \rfloor\) 分别表示对 \(c\) 向上取整和向下取整，例如：\(\lceil 2.1 \rceil = \lceil 2.9 \rceil = \lceil 3.0 \rceil = \lfloor 3.0 \rfloor = \lfloor 3.1 \rfloor = \lfloor 3.9 \rfloor = 3\)。

输出格式

对每个关卡依次输出一行答案。

输出的每一行包含一个正整数，表示相应的关卡中，消灭所有小猪最少需要的小鸟数量。

样例 #1

样例输入 #1
2
2 0
1.00 3.00
3.00 3.00
5 2
1.00 5.00
2.00 8.00
3.00 9.00
4.00 8.00
5.00 5.00
样例输出 #1
1
1
样例 #2

样例输入 #2
3
2 0
1.41 2.00
1.73 3.00
3 0
1.11 1.41
2.34 1.79
2.98 1.49
5 0
2.72 2.72
2.72 3.14
3.14 2.72
3.14 3.14
5.00 5.00
样例输出 #2
2
2
3
样例 #3

样例输入 #3
1
10 0
7.16 6.28
2.02 0.38
8.33 7.78
7.68 2.09
7.46 7.86
5.77 7.44
8.24 6.72
4.42 5.11
5.42 7.79
8.15 4.99
样例输出 #3
6
提示

【样例解释1】

这组数据中一共有两个关卡。

第一个关卡与【问题描述】中的情形相同，\(2\) 只小猪分别位于 \((1.00,3.00)\) 和 \((3.00,3.00)\)，只需发射一只飞行轨迹为 \(y = -x^2 + 4x\) 的小鸟即可消灭它们。

第二个关卡中有 \(5\) 只小猪，但经过观察我们可以发现它们的坐标都在抛物线 \(y = -x^2 + 6x\)上，故 Kiana 只需要发射一只小鸟即可消灭所有小猪。

【数据范围】

测试点编号 \(n\leqslant\) \(m=\) \(T\leqslant\)

\(1\) \(2\) \(0\) \(10\)

\(2\) \(2\) \(0\) \(30\)

\(3\) \(3\) \(0\) \(10\)

\(4\) \(3\) \(0\) \(30\)

\(5\) \(4\) \(0\) \(10\)

\(6\) \(4\) \(0\) \(30\)

\(7\) \(5\) \(0\) \(10\)

\(8\) \(6\) \(0\) \(10\)

\(9\) \(7\) \(0\) \(10\)

\(10\) \(8\) \(0\) \(10\)

\(11\) \(9\) \(0\) \(30\)

\(12\) \(10\) \(0\) \(30\)

\(13\) \(12\) \(1\) \(30\)

\(14\) \(12\) \(2\) \(30\)

\(15\) \(15\) \(0\) \(15\)

\(16\) \(15\) \(1\) \(15\)

\(17\) \(15\) \(2\) \(15\)

\(18\) \(18\) \(0\) \(5\)

\(19\) \(18\) \(1\) \(5\)

\(20\) \(18\) \(2\) \(5\)

测试点编号	\(n\leqslant\)	\(m=\)	\(T\leqslant\)
\(1\)	\(2\)	\(0\)	\(10\)
\(2\)	\(2\)	\(0\)	\(30\)
\(3\)	\(3\)	\(0\)	\(10\)
\(4\)	\(3\)	\(0\)	\(30\)
\(5\)	\(4\)	\(0\)	\(10\)
\(6\)	\(4\)	\(0\)	\(30\)
\(7\)	\(5\)	\(0\)	\(10\)
\(8\)	\(6\)	\(0\)	\(10\)
\(9\)	\(7\)	\(0\)	\(10\)
\(10\)	\(8\)	\(0\)	\(10\)
\(11\)	\(9\)	\(0\)	\(30\)
\(12\)	\(10\)	\(0\)	\(30\)
\(13\)	\(12\)	\(1\)	\(30\)
\(14\)	\(12\)	\(2\)	\(30\)
\(15\)	\(15\)	\(0\)	\(15\)
\(16\)	\(15\)	\(1\)	\(15\)
\(17\)	\(15\)	\(2\)	\(15\)
\(18\)	\(18\)	\(0\)	\(5\)
\(19\)	\(18\)	\(1\)	\(5\)
\(20\)	\(18\)	\(2\)	\(5\)

刚刚我写总结时突然发现，我赛时的做法时间复杂度就是正确的，只是我算错了而已🤣。

题目容易让人想到状压，然后设计 \(f_s\) 为击杀状态为 \(s\) 所需的数量，然后可以提前 \(O(n^3)\) 预处理每一条抛物线，具体的，枚举任意两个点然后推式子计算 \(a,b\)，再把 \(n\) 个点跑一遍看有多少个猪可以顺带打到就可以了。

后面有方程 \(f_{s|\text{line}}\gets\min(f_{s|\text{line}},f_s+1)\)。

可能是因为赛时紧张还是什么的，时间复杂度被我算成了 \(O(n^52^n)\)，实际上是 \(O(n^22^n)\)，这种粗心希望下次不要再犯了。

/**
 * @file 愤怒的小鸟.cpp 
 * @tag: #GMOJ#dp#状压dp#数学
 * @author: ZnPdCo
 * @date: 2024-01-11 20:57:17
 * @problem: https://gmoj.net/senior/#main/show/4908
 **/
#include <cstdio>
#include <cmath>
#include <algorithm>
#define ll long long
using namespace std;
#define N 20
ll T, n, m;
double x[N], y[N];
ll line[10*N], cnt;
ll f[1<<N];
int main() {
	freopen("angrybirds.in", "r", stdin);
	freopen("angrybirds.out", "w", stdout);
	scanf("%lld", &T);
	while(T--) {
		scanf("%lld %lld", &n, &m);
		for(ll i = 1; i <= n; i++) {
			scanf("%lf %lf", &x[i], &y[i]);
		}
		cnt = 0;
		for(ll i = 1; i <= n; i++) {
			for(ll j = i+1; j <= n; j++) if(x[i] != x[j] || y[i] != y[j]) {
/*
下面这个公式我数学不好，把推导放在这方便以后来看
$$
\because\begin{cases}
y_i=ax_i^2+bx_i \\
y_j=ax_j^2+bx_j
\end{cases} \\
\therefore\begin{cases}
\frac{y_i}{x_i}=ax_i+b \\
\frac{y_j}{x_j}=ax_j+b
\end{cases} \\
\therefore a(x_i-x_j)=\frac{y_i}{x_i}-\frac{y_j}{x_j} \\
\therefore a=(\frac{y_i}{x_i}-\frac{y_j}{x_j})\div(x_i-x_j) \\
\therefore b=\frac{y_i}{x_i}-ax_i
$$
*/
				double a = (y[i]/x[i]-y[j]/x[j])/(x[i]-x[j]);
				double b = y[i]/x[i]-a*x[i];
				if(a >= 0) continue;
				line[++cnt] = 0;
				for(ll k = 1; k <= n; k++) {
					if(abs(a*x[k]*x[k]+b*x[k]-y[k]) <= 1e-9) {
						line[cnt] |= (1<<(k-1));
					}
				}
			}
			
			
			line[++cnt] = 0;
			for(ll j = i+1; j <= n; j++) if(x[i] == x[j] && y[i] == y[j]) {
				line[cnt] |= (1<<(j-1));
			}
		}
		for(ll s = 1; s < (1<<n); s++) f[s] = 1e15;
		for(ll s = 0; s < (1<<n); s++) {
			for(ll i = 1; i <= cnt; i++) {
				f[s|line[i]] = min(f[s|line[i]], f[s] + 1);
			}
			for(ll i = 1; i <= n; i++) {
				f[s|(1<<(i-1))] = min(f[s|(1<<(i-1))], f[s] + 1);
			}
		}
		printf("%lld\n", f[(1<<n)-1]);
	}
}

T2 换教室

[NOIP2016 提高组] 换教室

题目背景

NOIP2016 提高组 D1T3

题目描述

对于刚上大学的牛牛来说，他面临的第一个问题是如何根据实际情况申请合适的课程。

在可以选择的课程中，有 \(2n\) 节课程安排在 \(n\) 个时间段上。在第 \(i\)（\(1 \leq i \leq n\)）个时间段上，两节内容相同的课程同时在不同的地点进行，其中，牛牛预先被安排在教室 \(c_i\) 上课，而另一节课程在教室 \(d_i\) 进行。

在不提交任何申请的情况下，学生们需要按时间段的顺序依次完成所有的 \(n\) 节安排好的课程。如果学生想更换第 \(i\) 节课程的教室，则需要提出申请。若申请通过，学生就可以在第 \(i\) 个时间段去教室 \(d_i\) 上课，否则仍然在教室 \(c_i\) 上课。

由于更换教室的需求太多，申请不一定能获得通过。通过计算，牛牛发现申请更换第 \(i\) 节课程的教室时，申请被通过的概率是一个已知的实数 \(k_i\)，并且对于不同课程的申请，被通过的概率是互相独立的。

学校规定，所有的申请只能在学期开始前一次性提交，并且每个人只能选择至多 \(m\) 节课程进行申请。这意味着牛牛必须一次性决定是否申请更换每节课的教室，而不能根据某些课程的申请结果来决定其他课程是否申请；牛牛可以申请自己最希望更换教室的 \(m\) 门课程，也可以不用完这 \(m\) 个申请的机会，甚至可以一门课程都不申请。

因为不同的课程可能会被安排在不同的教室进行，所以牛牛需要利用课间时间从一间教室赶到另一间教室。

牛牛所在的大学有 \(v\) 个教室，有 \(e\) 条道路。每条道路连接两间教室，并且是可以双向通行的。由于道路的长度和拥堵程度不同，通过不同的道路耗费的体力可能会有所不同。当第 \(i\)（\(1 \leq i \leq n-1\)）节课结束后，牛牛就会从这节课的教室出发，选择一条耗费体力最少的路径前往下一节课的教室。

现在牛牛想知道，申请哪几门课程可以使他因在教室间移动耗费的体力值的总和的期望值最小，请你帮他求出这个最小值。

输入格式

第一行四个整数 \(n,m,v,e\)。\(n\) 表示这个学期内的时间段的数量；\(m\) 表示牛牛最多可以申请更换多少节课程的教室；\(v\) 表示牛牛学校里教室的数量；\(e\) 表示牛牛的学校里道路的数量。

第二行 \(n\) 个正整数，第 \(i\)（\(1 \leq i \leq n\)）个正整数表示 \(c_i\)，即第 \(i\) 个时间段牛牛被安排上课的教室；保证 \(1 \le c_i \le v\)。

第三行 \(n\) 个正整数，第 \(i\)（\(1 \leq i \leq n\)）个正整数表示 \(d_i\)，即第 \(i\) 个时间段另一间上同样课程的教室；保证 \(1 \le d_i \le v\)。

第四行 \(n\) 个实数，第 \(i\)（\(1 \leq i \leq n\)）个实数表示 \(k_i\)，即牛牛申请在第 \(i\) 个时间段更换教室获得通过的概率。保证 \(0 \le k_i \le 1\)。

接下来 \(e\) 行，每行三个正整数 \(a_j, b_j, w_j\)，表示有一条双向道路连接教室 \(a_j, b_j\)，通过这条道路需要耗费的体力值是 \(w_j\)；保证 \(1 \le a_j, b_j \le v\)，\(1 \le w_j \le 100\)。

保证 \(1 \leq n \leq 2000\)，\(0 \leq m \leq 2000\)，\(1 \leq v \leq 300\)，\(0 \leq e \leq 90000\)。

保证通过学校里的道路，从任何一间教室出发，都能到达其他所有的教室。

保证输入的实数最多包含 \(3\) 位小数。

输出格式

输出一行，包含一个实数，四舍五入精确到小数点后恰好 \(2\) 位，表示答案。你的输出必须和标准输出完全一样才算正确。

测试数据保证四舍五入后的答案和准确答案的差的绝对值不大于 \(4 \times 10^{-3}\)。（如果你不知道什么是浮点误差，这段话可以理解为：对于大多数的算法，你可以正常地使用浮点数类型而不用对它进行特殊的处理）

样例 #1

样例输入 #1
3 2 3 3
2 1 2
1 2 1
0.8 0.2 0.5 
1 2 5
1 3 3
2 3 1
样例输出 #1
2.80
提示

样例 1 说明

所有可行的申请方案和期望收益如下：

不作申请，耗费的体力值的期望为 \(8.0\)。

申请通过的时间段出现的概率耗费的体力值

无 \(1.0\) \(8\)

申请更换第 \(1\) 个时间段的上课教室，耗费的体力值的期望为 \(4.8\)。

申请通过的时间段出现的概率耗费的体力值

\(1\) \(0.8\) \(4\)

无 \(0.2\) \(8\)

申请更换第 \(2\) 个时间段的上课教室，耗费的体力值的期望为 \(6.4\)。

申请通过的时间段出现的概率耗费的体力值

\(2\) \(0.2\) \(0\)

无 \(0.8\) \(8\)

申请更换第 \(3\) 个时间段的上课教室，耗费的体力值的期望为 \(6.0\)。

申请通过的时间段出现的概率耗费的体力值

\(3\) \(0.5\) \(4\)

无 \(0.5\) \(8\)

申请更换第 \(1,2\) 个时间段的上课教室，耗费的体力值的期望为 \(4.48\)。

申请通过的时间段出现的概率耗费的体力值

\(1,2\) \(0.16\) \(4\)

\(1\) \(0.64\) \(4\)

\(2\) \(0.04\) \(0\)

无 \(0.16\) \(8\)

申请更换第 \(1,3\) 个时间段的上课教室，耗费的体力值的期望为 \(2.8\)。

申请通过的时间段出现的概率耗费的体力值

\(1,3\) \(0.4\) \(0\)

\(1\) \(0.4\) \(4\)

\(3\) \(0.1\) \(4\)

无 \(0.1\) \(8\)

申请更换第 \(2,3\) 个时间段的上课教室，耗费的体力值的期望为 \(5.2\)。

申请通过的时间段出现的概率耗费的体力值

\(2,3\) \(0.1\) \(4\)

\(2\) \(0.1\) \(0\)

\(3\) \(0.4\) \(4\)

无 \(0.4\) \(8\)

因此，最优方案为：申请更换第 \(1,3\) 个时间段的上课教室。耗费的体力值的期望为 \(2.8\)。

提示

道路中可能会有多条双向道路连接相同的两间教室。也有可能有道路两端连接的是同一间教室。

请注意区分 \(n,m,v,e\) 的意义, \(n\) 不是教室的数量, \(m\) 不是道路的数量。

数据范围与说明

测试点编号 \(n\le\) \(m\le\) \(v\le\) 是否具有特殊性质 1 是否具有特殊性质 2

1 \(1\) \(1\) \(300\) \(\times\) \(\times\)

2 \(2\) \(0\) \(20\) \(\times\) \(\times\)

3 \(2\) \(1\) \(100\) \(\times\) \(\times\)

4 \(2\) \(2\) \(300\) \(\times\) \(\times\)

5 \(3\) \(0\) \(20\) \(\surd\) \(\surd\)

6 \(3\) \(1\) \(100\) \(\surd\) \(\times\)

7 \(3\) \(2\) \(300\) \(\times\) \(\times\)

8 \(10\) \(0\) \(300\) \(\surd\) \(\surd\)

9 \(10\) \(1\) \(20\) \(\surd\) \(\times\)

10 \(10\) \(2\) \(100\) \(\times\) \(\times\)

11 \(10\) \(10\) \(300\) \(\times\) \(\surd\)

12 \(20\) \(0\) \(20\) \(\surd\) \(\times\)

13 \(20\) \(1\) \(100\) \(\times\) \(\times\)

14 \(20\) \(2\) \(300\) \(\surd\) \(\times\)

15 \(20\) \(20\) \(300\) \(\times\) \(\surd\)

16 \(300\) \(0\) \(20\) \(\times\) \(\times\)

17 \(300\) \(1\) \(100\) \(\times\) \(\times\)

18 \(300\) \(2\) \(300\) \(\surd\) \(\surd\)

19 \(300\) \(300\) \(300\) \(\times\) \(\surd\)

20 \(2000\) \(0\) \(20\) \(\times\) \(\times\)

21 \(2000\) \(1\) \(20\) \(\times\) \(\times\)

22 \(2000\) \(2\) \(100\) \(\times\) \(\times\)

23 \(2000\) \(2000\) \(100\) \(\times\) \(\times\)

24 \(2000\) \(2000\) \(300\) \(\times\) \(\times\)

25 \(2000\) \(2000\) \(300\) \(\times\) \(\times\)

特殊性质 1：图上任意不同的两点 \(u,v\) 间，存在一条耗费体力最少的路径只包含一条道路。

特殊性质 2：对于所有的 \(1≤ i≤ n,\ k_i= 1\)。

申请通过的时间段	出现的概率	耗费的体力值
无	\(1.0\)	\(8\)

申请通过的时间段	出现的概率	耗费的体力值
\(1\)	\(0.8\)	\(4\)
无	\(0.2\)	\(8\)

申请通过的时间段	出现的概率	耗费的体力值
\(2\)	\(0.2\)	\(0\)
无	\(0.8\)	\(8\)

申请通过的时间段	出现的概率	耗费的体力值
\(3\)	\(0.5\)	\(4\)
无	\(0.5\)	\(8\)

申请通过的时间段	出现的概率	耗费的体力值
\(1,2\)	\(0.16\)	\(4\)
\(1\)	\(0.64\)	\(4\)
\(2\)	\(0.04\)	\(0\)
无	\(0.16\)	\(8\)

申请通过的时间段	出现的概率	耗费的体力值
\(1,3\)	\(0.4\)	\(0\)
\(1\)	\(0.4\)	\(4\)
\(3\)	\(0.1\)	\(4\)
无	\(0.1\)	\(8\)

申请通过的时间段	出现的概率	耗费的体力值
\(2,3\)	\(0.1\)	\(4\)
\(2\)	\(0.1\)	\(0\)
\(3\)	\(0.4\)	\(4\)
无	\(0.4\)	\(8\)

测试点编号	\(n\le\)	\(m\le\)	\(v\le\)	是否具有特殊性质 1	是否具有特殊性质 2
1	\(1\)	\(1\)	\(300\)	\(\times\)	\(\times\)
2	\(2\)	\(0\)	\(20\)	\(\times\)	\(\times\)
3	\(2\)	\(1\)	\(100\)	\(\times\)	\(\times\)
4	\(2\)	\(2\)	\(300\)	\(\times\)	\(\times\)
5	\(3\)	\(0\)	\(20\)	\(\surd\)	\(\surd\)
6	\(3\)	\(1\)	\(100\)	\(\surd\)	\(\times\)
7	\(3\)	\(2\)	\(300\)	\(\times\)	\(\times\)
8	\(10\)	\(0\)	\(300\)	\(\surd\)	\(\surd\)
9	\(10\)	\(1\)	\(20\)	\(\surd\)	\(\times\)
10	\(10\)	\(2\)	\(100\)	\(\times\)	\(\times\)
11	\(10\)	\(10\)	\(300\)	\(\times\)	\(\surd\)
12	\(20\)	\(0\)	\(20\)	\(\surd\)	\(\times\)
13	\(20\)	\(1\)	\(100\)	\(\times\)	\(\times\)
14	\(20\)	\(2\)	\(300\)	\(\surd\)	\(\times\)
15	\(20\)	\(20\)	\(300\)	\(\times\)	\(\surd\)
16	\(300\)	\(0\)	\(20\)	\(\times\)	\(\times\)
17	\(300\)	\(1\)	\(100\)	\(\times\)	\(\times\)
18	\(300\)	\(2\)	\(300\)	\(\surd\)	\(\surd\)
19	\(300\)	\(300\)	\(300\)	\(\times\)	\(\surd\)
20	\(2000\)	\(0\)	\(20\)	\(\times\)	\(\times\)
21	\(2000\)	\(1\)	\(20\)	\(\times\)	\(\times\)
22	\(2000\)	\(2\)	\(100\)	\(\times\)	\(\times\)
23	\(2000\)	\(2000\)	\(100\)	\(\times\)	\(\times\)
24	\(2000\)	\(2000\)	\(300\)	\(\times\)	\(\times\)
25	\(2000\)	\(2000\)	\(300\)	\(\times\)	\(\times\)

状态设计经验不足，其实我的状态太复杂导致不好推。

我设计的状态是 \(f_{第i节课,用了j次换课机会,这节课是否换课成功}\) 的最小期望值，这样设计就会导致我需要处理上节课是否换课，而是否成功存在后效性，导致无法做出。

其实题解的状态是 \(f_{第i节课,用了j次换课机会,这节课\mathbf{是否换课}}\) 的最小期望值，这样设计就只需要处理上节课是否换课成功，而这个概率已经由题目给出为 \(k\) 所以很容易。

训练时其实考虑过更换状态，但是后面并没有这么做。

/**
 * @file 换教室.cpp 
 * @tag: #GMOJ#dp
 * @author: ZnPdCo
 * @date: 2024-01-11 20:57:17
 * @problem: https://gmoj.net/senior/#main/show/4905
 **/
#include <cstdio>
#include <algorithm>
using namespace std;
#define ll long long
#define N 2010
#define V 310
ll n, m, v, e;
ll c[N], d[N];
double k[N];
int dis[V][V];
double ans = 1e15;
double f[N][N][2];
// 第i节课 换了j次 当前换没换
int main() {
	freopen("classroom.in", "r", stdin);
	freopen("classroom.out", "w", stdout);
	scanf("%lld %lld %lld %lld", &n, &m, &v, &e);
	for(ll i = 1; i <= n; i++) scanf("%lld", &c[i]);
	for(ll i = 1; i <= n; i++) scanf("%lld", &d[i]);
	for(ll i = 1; i <= n; i++) scanf("%lf", &k[i]);
	for(ll i = 1; i <= v; i++) {
		for(ll j = i+1; j <= v; j++) {
			dis[i][j] = dis[j][i] = 1e9;
		}
	}
	for(ll i = 1; i <= e; i++) {
		ll u, v, w;
		scanf("%lld %lld %lld", &u, &v, &w);
		if(w < dis[u][v]) {
			dis[u][v] = dis[v][u] = w;
		}
	}
	for(ll k = 1; k <= v; k++) {
		for(ll i = 1; i <= v; i++) {
			for(ll j = 1; j <= v; j++) {
				dis[i][j] = min(dis[i][j], dis[i][k]+dis[k][j]);
			}
		}
	}
	for(ll i = 1; i <= n; i++) {
		for(ll j = 0; j <= m; j++) {
			f[i][j][0] = f[i][j][1] = 1e15;
		}
	}
	f[1][0][0] = f[1][1][1] = 0;
	for(ll i = 2; i <= n; i++) {
		f[i][0][0] = f[i-1][0][0] + dis[c[i-1]][c[i]];
		for(ll j = 1; j <= m; j++) {
			f[i][j][0] = min(f[i-1][j][0] + dis[c[i-1]][c[i]],
				f[i-1][j][1] + k[i-1] * dis[d[i-1]][c[i]] + 
				(1-k[i-1]) * dis[c[i-1]][c[i]]);
			f[i][j][1] = min(f[i-1][j-1][0] + k[i] * dis[c[i-1]][d[i]] + 
				(1-k[i]) * dis[c[i-1]][c[i]],
				f[i-1][j-1][1] + k[i-1] * k[i] * dis[d[i-1]][d[i]] + 
				(1-k[i-1]) * k[i] * dis[c[i-1]][d[i]] + 
				k[i-1] * (1-k[i]) * dis[d[i-1]][c[i]] + 
				(1-k[i-1]) * (1-k[i]) * dis[c[i-1]][c[i]]);
		}
	}
	for(ll i = 0; i <= m; i++) {
		ans = min(ans, f[n][i][0]);
		ans = min(ans, f[n][i][1]);
	}
	printf("%.2lf", ans);
}

T3 天天爱跑步

[NOIP2016 提高组] 天天爱跑步

题目背景

NOIP2016 提高组 D1T2

题目描述

小 C 同学认为跑步非常有趣，于是决定制作一款叫做《天天爱跑步》的游戏。《天天爱跑步》是一个养成类游戏，需要玩家每天按时上线，完成打卡任务。

这个游戏的地图可以看作一棵包含 \(n\) 个结点和 \(n-1\) 条边的树，每条边连接两个结点，且任意两个结点存在一条路径互相可达。树上结点编号为从 \(1\) 到 \(n\) 的连续正整数。

现在有 \(m\) 个玩家，第 \(i\) 个玩家的起点为 \(s_i\)，终点为 \(t_i\)。每天打卡任务开始时，所有玩家在第 \(0\) 秒同时从自己的起点出发，以每秒跑一条边的速度，不间断地沿着最短路径向着自己的终点跑去，跑到终点后该玩家就算完成了打卡任务。（由于地图是一棵树，所以每个人的路径是唯一的）

小 C 想知道游戏的活跃度，所以在每个结点上都放置了一个观察员。在结点 \(j\) 的观察员会选择在第 \(w_j\) 秒观察玩家，一个玩家能被这个观察员观察到当且仅当该玩家在第 \(w_j\) 秒也正好到达了结点 \(j\)。小 C 想知道每个观察员会观察到多少人?

注意：我们认为一个玩家到达自己的终点后该玩家就会结束游戏，他不能等待一段时间后再被观察员观察到。即对于把结点 \(j\) 作为终点的玩家：若他在第 \(w_j\) 秒前到达终点，则在结点 \(j\) 的观察员不能观察到该玩家；若他正好在第 \(w_j\) 秒到达终点，则在结点 \(j\) 的观察员可以观察到这个玩家。

输入格式

第一行有两个整数 \(n\) 和 \(m\)。其中 \(n\) 代表树的结点数量, 同时也是观察员的数量, \(m\) 代表玩家的数量。

接下来 \(n-1\) 行每行两个整数 \(u\) 和 \(v\)，表示结点 \(u\) 到结点 \(v\) 有一条边。

接下来一行 \(n\) 个整数，其中第 \(j\) 个整数为 \(w_j\) , 表示结点 \(j\) 出现观察员的时间。

接下来 \(m\) 行，每行两个整数 \(s_i\)，和 \(t_i\)，表示一个玩家的起点和终点。

对于所有的数据，保证 \(1\leq s_i,t_i\leq n, 0\leq w_j\leq n\)。

输出格式

输出 \(1\) 行 \(n\) 个整数，第 \(j\) 个整数表示结点 \(j\) 的观察员可以观察到多少人。

样例 #1

样例输入 #1
6 3
2 3
1 2 
1 4 
4 5 
4 6 
0 2 5 1 2 3 
1 5 
1 3 
2 6
样例输出 #1
2 0 0 1 1 1
样例 #2

样例输入 #2
5 3 
1 2 
2 3 
2 4 
1 5 
0 1 0 3 0 
3 1 
1 4
5 5
样例输出 #2
1 2 1 0 1
提示

样例 1 说明

对于 \(1\) 号点，\(w_i=0\)，故只有起点为 \(1\) 号点的玩家才会被观察到，所以玩家 \(1\) 和玩家 \(2\) 被观察到，共有 \(2\) 人被观察到。

对于 \(2\) 号点，没有玩家在第 \(2\) 秒时在此结点，共 \(0\) 人被观察到。

对于 \(3\) 号点，没有玩家在第 \(5\) 秒时在此结点，共 \(0\) 人被观察到。

对于 \(4\) 号点，玩家 \(1\) 被观察到，共 \(1\) 人被观察到。

对于 \(5\) 号点，玩家 \(1\) 被观察到，共 \(1\) 人被观察到。

对于 \(6\) 号点，玩家 \(3\) 被观察到，共 \(1\) 人被观察到。

子任务

每个测试点的数据规模及特点如下表所示。

提示：数据范围的个位上的数字可以帮助判断是哪一种数据类型。

测试点编号 \(n=\) \(m=\) 约定

\(1\sim 2\) \(991\) \(991\) 所有人的起点等于自己的终点，即 \(\forall i,\ s_i=t_i\)

\(3\sim 4\) \(992\) \(992\) 所有 \(w_j=0\)

\(5\) \(993\) \(993\) 无

\(6\sim 8\) \(99994\) \(99994\) \(\forall i\in[1,n-1]\)，\(i\) 与 \(i+1\) 有边。即树退化成 \(1,2,\dots,n\) 按顺序连接的链

\(9\sim 12\) \(99995\) \(99995\) 所有 \(s_i=1\)

\(13\sim 16\) \(99996\) \(99996\) 所有 \(t_i=1\)

\(17\sim 19\) \(99997\) \(99997\) 无

\(20\) \(299998\) \(299998\) 无

提示

（提示：由于原提示年代久远，不一定能完全反映现在的情况，现在已经对该提示做出了一定的修改，提示的原文可以在该剪贴板查看）

在最终评测时，调用栈占用的空间大小不会有单独的限制，但在我们的工作环境中默认会有 \(1 \text{MiB}\) 的限制。这可能会引起函数调用层数较多时，程序发生栈溢出崩溃，程序中较深层数的递归往往会导致这个问题。如果你的程序需要用到较大的栈空间，请务必注意该问题。

我们可以使用一些方法修改调用栈的大小限制。

Linux

我们可以在终端中输入下列命令：ulimit -s 1048576。此命令的意义是，将调用栈的大小限制修改为 \(1048576\text{KiB}=1 \text{GiB}\)。

例如，对于如下程序 sample.cpp：
#include <bits/stdc++.h>
using namespace std;
int f[1000005];
void dfs(int a){
	if(a == 0){
		f[a] = 0;
		return;
	}
	dfs(a - 1);
	f[a] = f[a - 1] + 1;
}
int main(){
	dfs(1000000);
	return 0;
}
将上述源代码用命令 g++ sample.cpp -o sample 编译为可执行文件 sample 后，使用 ./sample 执行程序。

如果在没有使用命令 ulimit -s 1048576 的情况下运行该程序，sample 会因为栈溢出而崩溃；如果使用了上述命令后运行该程序，该程序则不会崩溃。

特别地，当你打开多个终端时，它们并不会共享该命令，你需要分别对它们运行该命令。

请注意，调用栈占用的空间会计入总空间占用中，和程序其他部分占用的内存共同受到内存限制。

Windows

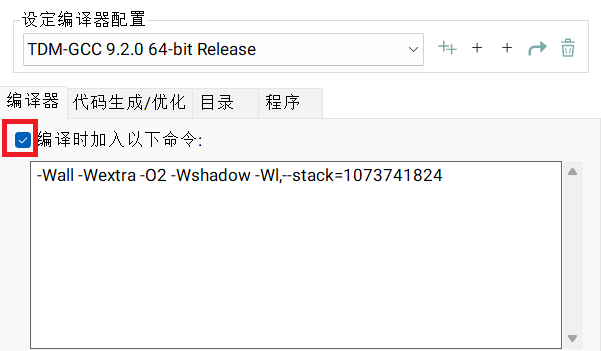
如果你使用 Windows 下的 Dev-C++，请选择 工具-编译选项 并在如下区域填入以下命令 -Wl,--stack=1073741824，填入后注意确认“编译时加入以下命令的”的框是已勾选状态。

此处 1073741824 的单位是 \(\text{B/Bytes}\)。

测试点编号	\(n=\)	\(m=\)	约定
\(1\sim 2\)	\(991\)	\(991\)	所有人的起点等于自己的终点，即 \(\forall i,\ s_i=t_i\)
\(3\sim 4\)	\(992\)	\(992\)	所有 \(w_j=0\)
\(5\)	\(993\)	\(993\)	无
\(6\sim 8\)	\(99994\)	\(99994\)	\(\forall i\in[1,n-1]\)，\(i\) 与 \(i+1\) 有边。即树退化成 \(1,2,\dots,n\) 按顺序连接的链
\(9\sim 12\)	\(99995\)	\(99995\)	所有 \(s_i=1\)
\(13\sim 16\)	\(99996\)	\(99996\)	所有 \(t_i=1\)
\(17\sim 19\)	\(99997\)	\(99997\)	无
\(20\)	\(299998\)	\(299998\)	无

以为是树链剖分，其实也好理解。

考虑把 \(s\to t\) 变成 \(s\to\text{lca}\to t\)，然后分成两个链。

网上推导很多了，在 \(s\to\text{lca}\) 中有 \(\text{dep}_s=\text{dep}_{\text{lca}}-w_{\text{lca}}\)；在 \(\text{lca}\to t\) 中有 \(\text{dist}_{s,t}-\text{dep}_t=w_{\text{lca}}-\text{dep}_{\text{lca}}\)。

明显可以放进桶内统计，困扰我的就是怎么保证 \(s,t\) 在 lca 子树内，这个可以用 dfs 时顺带处理，到达一个点后有添加操作，离开一个 lca 后有删除操作，记录差值即可。

/**
 * @file 天天爱跑步.cpp 
 * @tag: #GMOJ#桶#LCA
 * @author: ZnPdCo
 * @date: 2024-01-11 20:57:17
 * @problem: https://gmoj.net/senior/#main/show/4904
 **/
#include <cstdio>
#include <algorithm>
#include <vector>
#define ll long long
#define N 300000
using namespace std;
ll n, m;
ll head[N];
ll nxt[2*N];
ll to[2*N], cnt;
ll w[N], s[N], t[N];
ll ans[N];

void addEdge(ll u, ll v) {
	cnt++;
	to[cnt] = v;
	nxt[cnt] = head[u];
	head[u] = cnt;
}

ll f[N][30], dep[N];
ll logn[N];
void dfs(ll u, ll fa) {
	dep[u] = dep[fa] + 1;
	f[u][0] = fa;
	for(ll i = head[u]; i; i = nxt[i]) {
		ll v = to[i];
		if(v == fa) continue;
		dfs(v, u);
	}
}
ll LCA(ll x, ll y) {
	if(dep[x] < dep[y]) swap(x, y);
	while(dep[x] != dep[y]) x = f[x][logn[dep[x]-dep[y]]];
	if(x == y) return x;
	for(ll i = logn[dep[x]]; i >= 0; i--) {
		if(f[x][i] && f[y][i] && f[x][i] != f[y][i]) {
			x = f[x][i];
			y = f[y][i];
		}
	}
	return f[x][0];
}

vector<pair<ll, ll> > opt1[N], opt2[N];
ll b1[N], b2[2*N];
void dfs1(ll u, ll fa) {
	ll od = b1[dep[u]+w[u]];
	for(ll i = head[u]; i; i = nxt[i]) {
		ll v = to[i];
		if(v == fa) continue;
		dfs1(v, u);
	}
	for(auto x : opt1[u]) {
		b1[x.first] += x.second;
	}
	ll nw = b1[dep[u]+w[u]];
	ans[u] += nw-od;
}
void dfs2(ll u, ll fa) {
	ll od = b2[w[u]-dep[u]+N];
	for(ll i = head[u]; i; i = nxt[i]) {
		ll v = to[i];
		if(v == fa) continue;
		dfs2(v, u);
	}
	for(auto x : opt2[u]) {
		b2[x.first+N] += x.second;
	}
	ll nw = b2[w[u]-dep[u]+N];
	ans[u] += nw-od;
}

int main() {
	freopen("running.in", "r", stdin);
	freopen("running.out", "w", stdout);
	scanf("%lld %lld", &n, &m);
	logn[1] = 0;
	for(ll i = 2; i <= n; i++) {
		logn[i] = logn[i>>1]+1;
	}
	for(ll i = 1; i < n; i++) {
		ll u, v;
		scanf("%lld %lld", &u, &v);
		addEdge(u, v);
		addEdge(v, u);
	}
	dfs(1, 0);
	for(ll j = 1; j <= 20; j++) {
		for(ll i = 1; i <= n; i++) {
			f[i][j] = f[f[i][j-1]][j-1];
		}
	}
	for(ll i = 1; i <= n; i++) {
		scanf("%lld", &w[i]);
	}
	for(ll i = 1; i <= m; i++) {
		scanf("%lld %lld", &s[i], &t[i]);
		ll ca = LCA(s[i], t[i]);
		// dep_s=dep_{ca}-w_{ca}
		opt1[s[i]].push_back(make_pair(dep[s[i]], 1));	// 在到达s[i]时添加贡献
		opt1[ca].push_back(make_pair(dep[s[i]], -1));	// 在离开会统计s[i]的lca时删除贡献
	}
	dfs1(1, 0);
	for(ll i = 1; i <= m; i++) {
		ll ca = LCA(s[i], t[i]);
		ll dist = dep[s[i]] + dep[t[i]] - 2*dep[ca];
		// dist_{s,t}-w_{ca}=dep_t-dep_{ca}
		// dist_{s,t}-dep_t=w_{ca}-dep_{ca}
		opt2[t[i]].push_back(make_pair(dist - dep[t[i]], 1));		// 在到达t[i]时添加贡献
		opt2[f[ca][0]].push_back(make_pair(dist - dep[t[i]], -1));	// 在离开会统计t[i]的lca时删除贡献
		// 这里为了统计lca自己
	}
	dfs2(1, 0);
	for(ll i = 1; i <= n; i++) {
		printf("%lld ", ans[i]);
	}
}

T4 蚯蚓

[NOIP2016 提高组] 蚯蚓

题目背景

NOIP2016 提高组 D2T2

题目描述

本题中，我们将用符号 \(\lfloor c \rfloor\) 表示对 \(c\) 向下取整，例如：\(\lfloor 3.0 \rfloor = \lfloor 3.1 \rfloor = \lfloor 3.9 \rfloor = 3\)。

蛐蛐国最近蚯蚓成灾了！隔壁跳蚤国的跳蚤也拿蚯蚓们没办法，蛐蛐国王只好去请神刀手来帮他们消灭蚯蚓。

蛐蛐国里现在共有 \(n\) 只蚯蚓（\(n\) 为正整数）。每只蚯蚓拥有长度，我们设第 \(i\) 只蚯蚓的长度为 \(a_i\,(i=1,2,\dots,n)\)，并保证所有的长度都是非负整数（即：可能存在长度为 \(0\) 的蚯蚓）。

每一秒，神刀手会在所有的蚯蚓中，准确地找到最长的那一只（如有多个则任选一个）将其切成两半。神刀手切开蚯蚓的位置由常数 \(p\)（是满足 \(0 < p < 1\) 的有理数）决定，设这只蚯蚓长度为 \(x\)，神刀手会将其切成两只长度分别为 \(\lfloor px \rfloor\) 和 \(x - \lfloor px \rfloor\) 的蚯蚓。特殊地，如果这两个数的其中一个等于 \(0\)，则这个长度为 \(0\) 的蚯蚓也会被保留。此外，除了刚刚产生的两只新蚯蚓，其余蚯蚓的长度都会增加 \(q\)（是一个非负整常数）。

蛐蛐国王知道这样不是长久之计，因为蚯蚓不仅会越来越多，还会越来越长。蛐蛐国王决定求助于一位有着洪荒之力的神秘人物，但是救兵还需要 \(m\) 秒才能到来……（\(m\) 为非负整数）

蛐蛐国王希望知道这 \(m\) 秒内的战况。具体来说，他希望知道：

\(m\) 秒内，每一秒被切断的蚯蚓被切断前的长度（有 \(m\) 个数）；

\(m\) 秒后，所有蚯蚓的长度（有 \(n + m\) 个数）。

蛐蛐国王当然知道怎么做啦！但是他想考考你……

输入格式

第一行包含六个整数 \(n,m,q,u,v,t\)，其中：\(n,m,q\) 的意义见【问题描述】；\(u,v,t\) 均为正整数；你需要自己计算 \(p=u / v\)（保证 \(0 < u < v\)）；\(t\) 是输出参数，其含义将会在【输出格式】中解释。

第二行包含 \(n\) 个非负整数，为 \(a_1, a_2, \dots, a_n\)，即初始时 \(n\) 只蚯蚓的长度。

同一行中相邻的两个数之间，恰好用一个空格隔开。

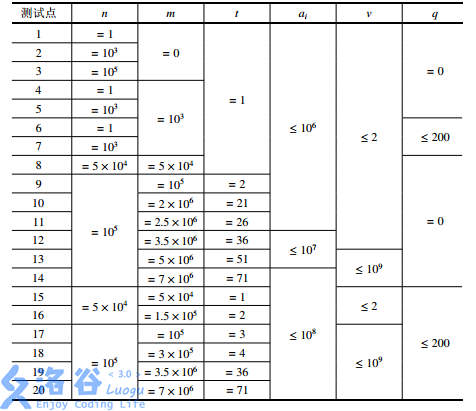
保证 \(1 \leq n \leq 10^5\)，\(0 \leq m \leq 7 \times 10^6\)，\(0 < u < v \leq 10^9\)，\(0 \leq q \leq 200\)，\(1 \leq t \leq 71\)，\(0 \leq a_i \leq 10^8\)。

输出格式

第一行输出 \(\left \lfloor \frac{m}{t} \right \rfloor\) 个整数，按时间顺序，依次输出第 \(t\) 秒，第 \(2t\) 秒，第 \(3t\) 秒，……被切断蚯蚓（在被切断前）的长度。

第二行输出 \(\left \lfloor \frac{n+m}{t} \right \rfloor\) 个整数，输出 \(m\) 秒后蚯蚓的长度；需要按从大到小的顺序，依次输出排名第 \(t\)，第 \(2t\)，第 \(3t\)，……的长度。

同一行中相邻的两个数之间，恰好用一个空格隔开。即使某一行没有任何数需要输出，你也应输出一个空行。

请阅读样例来更好地理解这个格式。

样例 #1

样例输入 #1
3 7 1 1 3 1
3 3 2
样例输出 #1
3 4 4 4 5 5 6
6 6 6 5 5 4 4 3 2 2
样例 #2

样例输入 #2
3 7 1 1 3 2
3 3 2
样例输出 #2
4 4 5
6 5 4 3 2
样例 #3

样例输入 #3
3 7 1 1 3 9
3 3 2
样例输出 #3
//空行
2
提示

样例解释 1

在神刀手到来前：\(3\) 只蚯蚓的长度为 \(3,3,2\)。

\(1\) 秒后：一只长度为 \(3\) 的蚯蚓被切成了两只长度分别为\(1\) 和 \(2\) 的蚯蚓，其余蚯蚓的长度增加了 \(1\)。最终 \(4\) 只蚯蚓的长度分别为 \((1,2),4,3\)。括号表示这个位置刚刚有一只蚯蚓被切断。

\(2\) 秒后：一只长度为 \(4\) 的蚯蚓被切成了 \(1\) 和 \(3\)。\(5\) 只蚯蚓的长度分别为：\(2,3,(1,3),4\)。

\(3\) 秒后：一只长度为 \(4\) 的蚯蚓被切断。\(6\) 只蚯蚓的长度分别为：\(3,4,2,4,(1,3)\)。

\(4\) 秒后：一只长度为 \(4\) 的蚯蚓被切断。\(7\) 只蚯蚓的长度分别为：\(4,(1,3),3,5,2,4\)。

\(5\) 秒后：一只长度为 \(5\) 的蚯蚓被切断。\(8\) 只蚯蚓的长度分别为：\(5,2,4,4,(1,4),3,5\)。

\(6\) 秒后：一只长度为 \(5\) 的蚯蚓被切断。\(9\) 只蚯蚓的长度分别为：\((1,4),3,5,5,2,5,4,6\)。

\(7\) 秒后：一只长度为 \(6\) 的蚯蚓被切断。\(10\) 只蚯蚓的长度分别为：\(2,5,4,6,6,3,6,5,(2,4)\)。所以，\(7\) 秒内被切断的蚯蚓的长度依次为 \(3,4,4,4,5,5,6\)。\(7\) 秒后，所有蚯蚓长度从大到小排序为 \(6,6,6,5,5,4,4,3,2,2\)。

样例解释 2

这个数据中只有 \(t=2\) 与上个数据不同。只需在每行都改为每两个数输出一个数即可。

虽然第一行最后有一个 \(6\) 没有被输出，但是第二行仍然要重新从第二个数再开始输出。

样例解释 3

这个数据中只有 \(t=9\) 与上个数据不同。

注意第一行没有数要输出，但也要输出一个空行。

数据范围

以为是水题，没看数据范围打了一个 \(O((n+m)\log (n+m))\) 的做法，对于全局加可以看作是自己减。

中午没看题解回去躺在床上自己就想到了线性做法，以后做题时一定要测极限数据呀！

然后可以感性理解线性做法，先不看每次生长的 \(q\)，每次取出的会被分裂，所以长度一定是越来越短，可以维护三个队列来做，分别储存原本的，分裂的较大部分，分裂较小部分，然后每次长度肯定是队列中最短的，所以可以放心加到队尾。

至于生长的 \(q\)，同理可以看作是自己减。

/**
 * @file 蚯蚓.cpp 
 * @tag: #GMOJ#队列#数学
 * @author: ZnPdCo
 * @date: 2024-01-11 20:57:17
 * @problem: https://gmoj.net/senior/#main/show/4907
 **/
#include <cstdio>
#include <algorithm>
using namespace std;
#define ll long long
#define N 8000010
ll n, m, q, u, v, t;

ll a1[N], h1=1, t1, a2[N], h2=1, t2, a3[N], h3=1, t3, tot;
bool cmp(ll x, ll y) {
	return x > y;
}
int main() {
	freopen("earthworm.in", "r", stdin);
	freopen("earthworm.out", "w", stdout);
	
	scanf("%lld %lld %lld %lld %lld %lld", &n, &m, &q, &u, &v, &t);
	for(ll i = 1; i <= n; i++) {
		scanf("%lld", &a1[++t1]);
	}
	sort(a1+1, a1+1+n, cmp);
	for(ll i = 1; i <= m; i++) {
		ll head1 = h1<=t1?a1[h1] + q*(i-1):-1;
		ll head2 = h2<=t2?a2[h2] + q*(i-1):-1;
		ll head3 = h3<=t3?a3[h3] + q*(i-1):-1;
		if(head1 >= head2 && head1 >= head3) {
			if(i % t == 0) printf("%lld ", head1);
			h1++;
			a2[++t2] = head1 * u / v - q*i;
			a3[++t3] = head1 - head1 * u / v - q*i;
		} else if(head2 >= head1 && head2 >= head3) {
			if(i % t == 0) printf("%lld ", head2);
			h2++;
			a2[++t2] = head2 * u / v - q*i;
			a3[++t3] = head2 - head2 * u / v - q*i;
		} else {
			if(i % t == 0) printf("%lld ", head3);
			h3++;
			a2[++t2] = head3 * u / v - q*i;
			a3[++t3] = head3 - head3 * u / v - q*i;
		}
	}
	printf("\n");
	for(ll i = 1; i <= n+m; i++) {
		ll head1 = h1<=t1?a1[h1] + q*m:-1;
		ll head2 = h2<=t2?a2[h2] + q*m:-1;
		ll head3 = h3<=t3?a3[h3] + q*m:-1;
		if(head1 >= head2 && head1 >= head3) {
			if(i % t == 0) printf("%lld ", head1);
			h1++;
		} else if(head2 >= head1 && head2 >= head3) {
			if(i % t == 0) printf("%lld ", head2);
			h2++;
		} else {
			if(i % t == 0) printf("%lld ", head3);
			h3++;
		}
	}
}

posted @ 2024-01-11 21:00 ZnPdCo 阅读(17) 评论(0) 编辑收藏举报

刷新页面返回顶部

znpdco

2024-01-11 训练总结

T1 愤怒的小鸟

[NOIP2016 提高组] 愤怒的小鸟

题目背景

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

样例 #3

样例输入 #3

样例输出 #3

提示

T2 换教室

[NOIP2016 提高组] 换教室

题目背景

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

T3 天天爱跑步

[NOIP2016 提高组] 天天爱跑步

题目背景

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

提示

T4 蚯蚓

[NOIP2016 提高组] 蚯蚓

题目背景

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

样例 #3

样例输入 #3

样例输出 #3

提示

公告