20230818比赛
T1 休息(rest)
Description
休息的时候,可以放松放松浑身的肌肉,打扫打扫卫生,感觉很舒服。在某一天,某LMZ 开始整理他那书架。已知他的书有n 本,从左到右按顺序排列。他想把书从矮到高排好序,而每一本书都有一个独一无二的高度Hi。他排序的方法是:每一次将所有的书划分为尽量少的连续部分,使得每一部分的书的高度都是单调下降,然后将其中所有不少于2 本书的区间全部翻转。重复执行以上操作,最后使得书的高度全部单调上升。可是毕竟是休息时间,LMZ 不想花太多时间在给书排序这种事上面。因此他划分并翻转完第一次书之后,他想计算,他一共执行了多少次翻转操作才能把所有的书排好序。LMZ 惊奇地发现,第一次排序之前,他第一次划分出来的所有区间的长度都是偶数。
Input
第一行一个正整数n, 为书的总数。
接下来一行n个数,第i个正整数Hi,为第i 本书的高度。
Output
仅一个整数,为LMZ 需要做的翻转操作的次数。
Sample Input
6 5 3 2 1 6 4 Sample Output
3 【样例解释】 第一次划分之后,翻转(5,3,2,1),(6,4)。之后,书的高度为1 2 3 5 4 6,然后便是翻转(5,4)即可。 Data Constraint
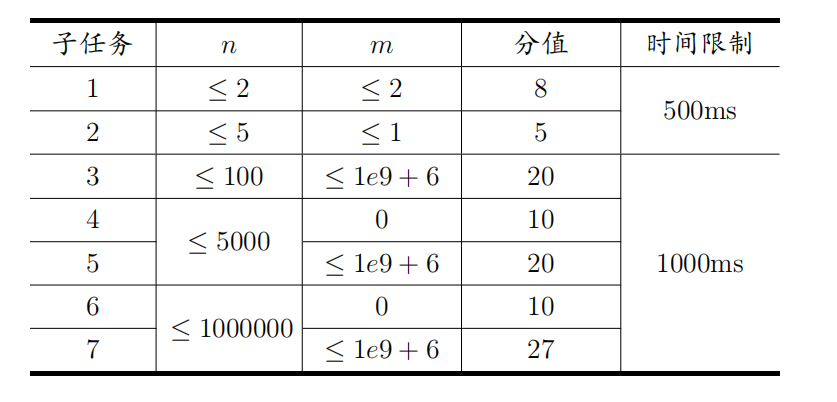
对于10%的数据:n<=50
对于40%的数据:n<=3000
对于100%的数据:1<=n<=100000, 1<=Hi<=n
首先我们先按题目要求翻转一次所有单调下降的连续部分,然后我们就可以知道,原本的乱序瞬间变成了:

那么我们会互相交换的也就只有以下红色部分或者紫色部分:

即因为已经翻转过一次所有单调下降的连续部分了,所以变得有序,也就是说,只有两个小区间之间的数可以进行交换。
这是什么?比赛时的我不知道,于是打了暴力。原来这是逆序对。(洛谷 P1908)
总结:对这种基础的知识不了解导致思路错误。
#include <cstdio> #include <algorithm> #define ll long long #define reg register using namespace std; ll n; ll a[100010]; ll b[100010]; ll ans; void solve(ll l, ll r) { if(l == r) return; ll mid = (l + r) >> 1; solve(l, mid); solve(mid + 1, r); ll pos1 = l, pos2 = mid + 1; for(ll i = l; i <= r; i++) { if(pos1 > mid) { b[i] = a[pos2++]; } else if(pos2 > r) { b[i] = a[pos1++]; } else if(a[pos1] > a[pos2]) { b[i] = a[pos1++]; ans += r - pos2 + 1; } else if(a[pos2] <= a[pos2]) { b[i] = a[pos2++]; } } for(ll i = l; i <= r; i++) { a[i] = b[i]; } } int main() { scanf("%lld", &n); for(ll i = 1; i <= n; i++) { scanf("%lld", &a[i]); } a[n + 1] = 1000000; ll pos = 1; for(ll i = 1; i <= n; i++) { if(a[i] < a[i + 1]) { if(pos != i) { ll l = pos, r = i; while(l <= r) { swap(a[l], a[r]); l++, r--; } ans++; } pos = i + 1; } } solve(1, n); printf("%lld", ans); }
T2 军训(training)
Description
HYSBZ 开学了!今年HYSBZ 有n 个男生来上学,学号为1…n,每个学生都必须参加军训。在这种比较堕落的学校里,每个男生都会有Gi 个女朋友,而且每个人都会有一个欠扁值Hi。学校为了保证军训时教官不会因为学生们都是人生赢家或者是太欠扁而发生打架事故,所以要把学生们分班,并做出了如下要求:
1.分班必须按照学号顺序来,即不能在一个班上出现学号不连续的情况。
2.每个学生必须要被分到某个班上。
3.每个班的欠扁值定义为该班中欠扁值最高的那名同学的欠扁值。所有班的欠扁值之和不得超过Limit。
4.每个班的女友指数定义为该班中所有同学的女友数量之和。在满足条件1、2、3 的情况下,分班应使得女友指数最高的那个班的女友指数最小。
请你帮HYSBZ 的教务处完成分班工作,并输出女友指数最高的班级的女友指数的最小值。
输入数据保证题目有解。
Input
第一行仅2 个正整数n, Limit,分别为学生数量和欠扁值之和的上限。
接下来n 行每行2 个正整数Hi,Gi,分别为学号为i 的学生的欠扁值和女友数。
Output
仅1 个正整数,表示满足分班的条件下,女友指数最高的班级的女友指数的最小值。
Sample Input
4 6 4 3 3 5 2 2 2 4 Sample Output
8 【样例解释】 分班按照(1,2),(3,4)进行,这时班级欠扁值之和为4+2=6<=Limit,而女友指数最高的班级为(1,2),为8。容易看出该分班方案可得到最佳答案。 Data Constraint
对于20%的数据:n,Limit<=100
对于40%的数据:n<=1000
对于100%的数据:1<=n,Gi<=20000,1<=Hi,Limit<=10^7
这种求最小的最大值能用什么?——二分(今天我才知道)
二分查找后我们需要维护一个 \(p\) 。看了网上大部分题解都没有讲清楚 \(p\) 是什么,后面我想了想应该是分割点。
如果没有看过网上的题解那我来说一下。首先,对于一个区间如果只看欠扁值,那么肯定是这个班级人越多越好,这个感性理解。二分出最大的女友指数 \(x\) 后我们需要确保没有区间比这个女友指数更大。不然 \(x\) 就不是最大的女友指数了。
那么我们保确女友指数在 \(x\) 内后,我们需要让这个班级人越多越好,那么我们维护一个 \(p\) 表示这个班级的第一个人(也就是学号最小的那个人,也就是上文的分割点),如果 \(\sum_{i=p}^{now} g_i\) 大于了 \(x\) ,那么就要把第一个人 \(p\) 从这个班里踢出,即 p++。
紧接着,因为我们要求出这个班内最大的欠扁值 \(h_{max}\) ,我们可以选择很多方式求出 \(p\cdots i\) 的最大欠扁值,可以选择 线段树、树状数组、st表、单调队列、暴力(?) 解决。
最后可以得到前 \(i\) 人分好班后的欠扁值之和为:
可以用单调队列优化。
#include <cstdio> #include <algorithm> #define ll long long using namespace std; ll n, lim; ll h[20010]; ll g[20010]; ll s[20010]; ll head, tail, p; ll q[20010]; ll f[20010]; bool check(ll x) { head = 1, tail = 0, p = 1; for(ll i = 1; i <= n; i++) { while(s[i] - s[p - 1] > x) p++; while(head <= tail && q[head] < p) head++; // 没有用的点 while(head <= tail && h[i] >= h[q[tail]]) tail--; // 维持单调性 q[++tail] = i; f[i] = f[p - 1] + h[q[head]]; for(ll j = head; j < tail; j++) { f[i] = min(f[i], f[q[j]] + h[q[j + 1]]); } if(f[i] > lim) return false; } return true; } int main() { scanf("%lld %lld", &n, &lim); for(ll i = 1; i <= n; i++) { scanf("%lld %lld", &h[i], &g[i]); s[i] = s[i - 1] + g[i]; } ll l = 0, r = s[n], ans; while(l <= r) { ll mid = (l + r) >> 1; if(check(mid)) { ans = mid; r = mid - 1; } else { l = mid + 1; } } printf("%lld", ans); }
T3 轻轨([USACO09FEB] Fair Shuttle G)
Description
有N(1<=N<=20,000)个站点的轻轨站,有一个容量为C(1<=C<=100)的列车起点在1号站点,终点在N号站点,有K(K<=50,000)组牛群,每组数量为M_i(1<=M_i<=N),行程起点和终点分别为S_i和E_i(1<=S_i<E_i<=N)
计算最多有多少头牛可以搭乘轻轨。允许小组里的一部分奶牛分开乘坐班车Input
第1行:3个空格隔开的整数K,N,C
第2到K+1行:描述每组奶牛的情况,每行3个空格隔开的整数S_i,E_i和M_iOutput
输出一个整数表示最多可以搭乘轻轨的牛的数量。
Sample Input
8 15 3 1 5 2 13 14 1 5 8 3 8 14 2 14 15 1 9 12 1 12 15 2 4 6 1 Sample Output
10 Data Constraint
Hint
【样例说明】
轻轨从1号站搭2头牛到5号站,搭3头牛从5好站到8号站,2头牛从8号站到14号站,1头牛从9号站到12号站,1头牛从13号站到14号站,1头牛从14号站到15号站。
洛谷版题目:
[USACO09FEB] Fair Shuttle G
题面翻译
逛逛集市,兑兑奖品,看看节目对农夫约翰来说不算什么,可是他的奶牛们非常缺乏锻炼——如果要逛完一整天的集市,他们一定会筋疲力尽的。所以为了让奶牛们也能愉快地逛集市,约翰准备让奶牛们在集市上以车代步。但是,约翰木有钱,他租来的班车只能在集市上沿直线跑一次,而且只能停靠 \(N(1 \leq N\leq 20000)\) 个地点(所有地点都以 \(1\) 到 \(N\) 之间的一个数字来表示)。现在奶牛们分成 \(K(1\leq K\leq 50000)\) 个小组,第i 组有 \(M_i(1\leq M_i\leq N)\) 头奶牛,他们希望从 \(S_i\) 跑到 \(E_i(1\leq S_i< E_i\leq N)\)。
由于班车容量有限,可能载不下所有想乘车的奶牛们,此时也允许小组里的一部分奶牛分开乘坐班车。约翰经过调查得知班车的容量是 \(C(1\leq C\leq 100)\),请你帮助约翰计划一个尽可能满足更多奶牛愿望的方案。
题目描述
Although Farmer John has no problems walking around the fair to collect prizes or see the shows, his cows are not in such good shape; a full day of walking around the fair leaves them exhausted. To help them enjoy the fair, FJ has arranged for a shuttle truck to take the cows from place to place in the fairgrounds.
FJ couldn't afford a really great shuttle, so the shuttle he rented traverses its route only once (!) and makes N (1 <= N <= 20,000) stops (conveniently numbered 1..N) along its path. A total of K (1 <= K <= 50,000) groups of cows conveniently numbered 1..K wish to use the shuttle, each of the M_i (1 <= M_i <= N) cows in group i wanting to ride from one stop S_i (1 <= S_i < E_i) to another stop E_i (S_i < E_i <= N) farther along the route.
The shuttle might not be able to pick up an entire group of cows (since it has limited capacity) but can pick up partial groups as appropriate.
Given the capacity C (1 <= C <= 100) of the shuttle truck and the descriptions of the groups of cows that want to visit various sites at the fair, determine the maximum number of cows that can ride the shuttle during the fair.
输入格式
第一行:包括三个整数:\(K,N\) 和 \(C\),彼此用空格隔开。
第二行到 \(K+1\) 行:在第 \(i+1\) 行,将会告诉你第 \(i\) 组奶牛的信息:\(S_i,E_i\) 和 \(M_i\),彼此用空格隔开。
输出格式
第一行:可以坐班车的奶牛的最大头数。
样例 #1
样例输入
8 15 3 1 5 2 13 14 1 5 8 3 8 14 2 14 15 1 9 12 1 12 15 2 4 6 1 样例输出 #1
10 提示
【样例说明】
班车可以把 \(2\) 头奶牛从 \(1\) 送到 \(5\),\(3\) 头奶牛从 \(5\) 送到 \(8\),\(2\) 头奶牛从 \(8\) 送到 \(14\),\(1\) 头奶牛从 \(9\) 送到 \(12\),\(1\) 头奶牛从 \(13\) 送到 \(14\),\(1\) 头奶牛从 \(14\) 送到 \(15\)。
为什么wa了呢?
因 为 题 目 出 错 啦………………题目漏了个“允许小组里的一部分奶牛分开乘坐班车”(现在应该补上了)
比赛时第一反应就是贪心,结果看到没有允许分开,以为要dp。于是打了个很丑陋的dp:
发现是个我不可做题(可能可以出一道新题目)
如果允许贪心就很简单了。
类比演讲安排,按结束时间排序,但是需要修改。
先是枚举到第几个奶牛区间,然后计算出最多可以添加多少牛(就是判断 \([st, ed)\) 区间的最大值,然后用 \(c\) 减去就是可搭乘的最小值)
如果大于当前组的牛的数量,那么就全上,把整个区间添加这个牛的数量。
如果小于,那么就上最多可以添加牛的数量,把整个区间添加这个牛的数量。
有线段树等做法,但是我懒……
所以我打了个暴力:
然后就有 94.1 pts了?
Why?
于是我又加了一个判断,判断如果当前数量大于等于 \(c\) 的话,就 continue。
然后就A了……
#include <cstdio> #include <algorithm> #define ll long long using namespace std; ll k, n, c, ans; struct node { ll s, e, m; } a[50010], b[50010]; ll num[50010]; bool cmp(node x, node y) { if(x.e == y.e) return x.s > y.s; return x.e < y.e; } void solve(ll l, ll r) { if(l == r) return; ll mid = (l + r) >> 1; solve(l, mid); solve(mid + 1, r); ll pos1 = l, pos2 = mid + 1; for(ll i = l; i <= r; i++) { if(pos1 > mid) { b[i] = a[pos2++]; } else if(pos2 > r) { b[i] = a[pos1++]; } else if(cmp(a[pos1], a[pos2])) { b[i] = a[pos1++]; } else { b[i] = a[pos2++]; } } for(ll i = l; i <= r; i++) { a[i] = b[i]; } } int main() { scanf("%lld %lld %lld", &k, &n, &c); for(ll i = 1; i <= k; i++) { scanf("%lld %lld %lld", &a[i].s, &a[i].e, &a[i].m); } solve(1, k); for(ll i = 1; i <= k; i++) { if(num[a[i].s] < c) { // 可以添加牛 ll mn = 1e15; for(ll j = a[i].s; j < a[i].e; j++) { // 计算出最多可以添加多少牛 mn = min(mn, c - num[j]); } if(mn > 0) { if(mn >= a[i].m) { // 加的空间大于实际牛 for(ll j = a[i].s; j < a[i].e; j++) { // 全加进去 num[j] += a[i].m; } ans += a[i].m; } else { for(ll j = a[i].s; j < a[i].e; j++) { // 只加一部分 num[j] += mn; } ans += mn; } } } } printf("%lld", ans); }
T4 幂矩阵 GMOJ 6405
Description
我们定义n阶m级Pascal幂矩阵如下:
举个例子, 2阶0级和3阶1级Pascal幂矩阵如下:
现在,请你求n阶m级Pascal幂矩阵的逆矩阵的各个元素的平方和(对1e9+
7取模).注:若矩阵B满足AB = BA = I, 那么称B为A的逆矩阵(其中I为单位矩
阵).
Input
从文件c.in中读入数据.
不行一个正整数n和一个自然数m.Output
输出到文件c.out中.
上行, 一个数表示答案.Sample Input
2 1 Sample Output
21 Data Constraint
(upd:20230820补完了)
我不多讲,具体看题解pdf,题解讲得非常清楚,就是我太弱,下面附上题解,最后就是我的补充:

大家应该是在这个地方出的问题:
我们看一看 \(m = 0\) 的情况。
由于我太蒟蒻,所以我只会反过来计算的方法。即我们已经知道逆矩阵的计算公式:
然后把这个代入回去,来证明它。
所以怎么代入呢?我们知道,一个矩阵乘以它的逆矩阵为单位矩阵 \(I\) 。关于单位矩阵,请百度(因为我懒)
出题人通过一个 \(A = P_n^{-1}P_n\) ,通过证明出 \(A = I\) 来得出逆矩阵的计算公式是正确的。
那么问题就来了,出题人怎么得出这个公式的(雾)
好的,按照题目的说法,设 \(A = P_n^{-1}P_n,i\ge j\) ,然后第一步是矩阵乘法定义(人家乘法就是这个公式),关于矩阵乘法,请百度(我懒)
那么有:
然后我们把 \((P_n)(k,j)\) 代入题目定义得出(注意我们已经设定 m = 0)
另外,根据出题人计算出的逆矩阵公式有:
然后我们知道:
同时消去:
那么上图问号处我们就需要填一些东西,凑出另外一对组合数。
那么我们知道:
其中的 \(n=m+(n-m)\)
那么此处我们应该也用相同的方式凑出来,例如用 \(j!\) 和 \((k-j)!\) 凑。但是我们发现会凑出 \(k\) ,这个已经凑过了(原式就是 \(k!\)),我们换一种方式:用 \((i-k)!\) 和 \((k-j)!\) 凑出 \((i-j)!\):
然后换一下顺序:
凑出:
代回去得到:
因为 \(\tbinom{i}{j}\) 和 \(\sum\) 并不相关(\(\sum\) 内枚举的是 \(k\))
所以可以提出来:
再拆开负一次方:
把与 \(\sum\) 不相关的 \((-1)^{i+j}\) 提出:
接着我们把 \(k=j\) 变为 \(k=0\) :
最后我们使用二项式定理(证明这个,请百度,或者以后我再看能不能写):
我们会发现,\(\sum_{k=0}^{i-j}(-1)^{k}\cdot \tbinom{i - j}{k}\) 。这里 \(\sum\) 有了(\(\sum_{k=0}^{i-j}\)), \(b^r\) 有了 (\((-1)^{k}\)),\(\tbinom{n}{r}\) 有了 (\(\tbinom{i - j}{k}\)),还差一个 \(a^{n-r}\) 。加上什么既可以满足这个 \(a^{n-r}\) 又可以不影响结果呢?
对了,是:
有了这个,我们可以得到:
即:
我们知道,在组合数学中, \(0^0=1\) ,其它情况为0。那么这不就是当 \(i=j\) 时 \(0^{i-j}\) 为1,当 \(i\not=j\) 时 \(0^{i-j}\) 为0吗。
所以我们用中括号表示逻辑,当中括号内为真,则中括号值为1,反之为0。
然后因为 \(i\not=j\) 时这个式子恒为0,所以有:
因为 \(i=j\):
这不就是单位矩阵吗?所以得证,上面的逆矩阵计算公式是正确的。
证毕。
接着我们看题解中没有说的 \(m\not=0\) :
一样的,还是要反过来证明:
同样设 \(A = P_n^{-1}P_n,i\ge j\),然后我们套一套上面的。
证毕
然后我们要用 \(n^2\) 是不太好的,我们一行一行看,某一行的平方和为:
那么有:
首先我们有 \(\tbinom{n}{m}=\tbinom{n}{n-m}\)
证明很简单:
所以有:
所以有:
很容易可以得到
所以:
关于 \(\tbinom{n}{0}\tbinom{n}{n}+\tbinom{n}{1}\tbinom{n}{n-1}+\tbinom{n}{2}\tbinom{n}{n-2}+\cdots+\tbinom{n}{n}\tbinom{n}{0}=\tbinom{2n}{n}\) 。我们可以以一种不那么严谨的方式证明。
假设我们有 \(2n\) 个小朋友,我们从中抽选 \(n\) 个小朋友,组合数为 \(\tbinom{2n}{n}\)
换一种方式,我们把这 \(2n\) 个小朋友分成两部分,每份有 \(n\) 个小朋友,我们从中抽选 \(n\) 个小朋友可以的方式有:
从第一组抽 \(0\) 个小朋友和从第二组抽 \(n\) 个小朋友
从第一组抽 \(1\) 个小朋友和从第二组抽 \(n-1\) 个小朋友
从第一组抽 \(2\) 个小朋友和从第二组抽 \(n-2\) 个小朋友
\(\cdots\)
从第一组抽 \(n-1\) 个小朋友和从第二组抽 \(1\) 个小朋友
从第一组抽 \(n\) 个小朋友和从第二组抽 \(0\) 个小朋友
全部的情况数加起来就是 \(\tbinom{2n}{n}\) 啦lol。
回到:
根据 \(\sum_{j=0}^i\tbinom{i}{j}^2=\tbinom{2i}{i}\)
所以:
最终得到第 \(i\) 行的平方和为:
枚举第 \(i\) 行计算,然后就a啦!!!
耶!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
#include <cstdio> #define ll long long #define P ((ll)1e9+7) ll n, m; ll ans; ll i2Fact = 1; ll iiFact = 1; ll qpow(ll x, ll y) { if(y == 0) return 1; if(y % 2 == 0) { ll res = qpow(x, y / 2); return res * res % P; } return qpow(x, y - 1) * x % P; } int main() { freopen("c.in", "r", stdin); freopen("c.out", "w", stdout); scanf("%lld %lld", &n, &m); for(ll i = 1; i <= n; i++) { (i2Fact *= (2 * i - 1) % P * (2 * i) % P) %= P; (iiFact *= (i % P * i % P)) %= P; (ans += qpow(i, 2 * m) * (((i2Fact * qpow(iiFact, P - 2) % P) - 1) % P + P % P)) %= P; } printf("%lld", ans); }





· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 按钮权限的设计及实现