20230816比赛
T1 矩形
Description
现在我们在一个平面上画了n个矩形。每一个矩形的两边都与坐标轴相平行,且矩形定点的坐标均为整数。现我们定义满足如下性质的图形为一个块:
每一个矩形都是一个块;
如果两个块有一段公共的部分,那么这两个块就会形成一个新的块,否则这两个块就是不同的。
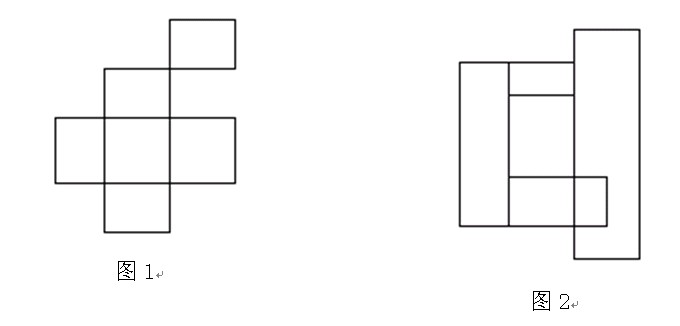
示例:
图1中的矩形形成了两个不同的块。
图2中的矩形形成了一个块。
任务:
请写一个程序:
从文本文件PRO.IN中读入各个矩形的顶点坐标;
找出这些矩形中不同的块的数目;
把结果输出到文本文件PRO.OUT中。
Input
在输入文件PRO.IN的第一行又一个整数n,1 <= n <=7000,表示矩形的个数。接下来的n行描述矩形的顶点,每个矩形用四个数来描述:左下顶点坐标(x,y)与右上顶点坐标(x,y)。每个矩形的坐标都是不超过10000的非负整数。
Output
输出唯一的一个整数——这些矩形所形成的不同的块的数目。
Sample Input
9 0 3 2 6 4 5 5 7 4 2 6 4 2 0 3 2 5 3 6 4 3 2 5 3 1 4 4 7 0 0 1 4 0 0 4 1Sample Output
2Data Constraint
数据规模
对于60%的数据,有N<=80
对于100%的数据如题目。
一眼冰茶几(并查集),枚举两个矩形,如果这两个矩形存在公告部分就可以加入并查集。
问题就是怎么判存在公共部分。
我定义了以下函数:
-
check1用于检查 a 的 x1 或 x2 在 b 的 x1 到 x2 中间+--+ |b | +--+-+| | a| || +--+-+| | | +--+ -
check2用于检查 a 的 y1 或 y2 在 b 的 y1 到 y2 中间+--+ |a | +--+--+--+ | | | | | +--+b | +--------+ -
check3用于检查 a 的 端点 与 b 的 端点 重合+--+ |a | +--+--+ | | | b| +--+ -
inside用于检查 a 在 b 的内部,防止check3误判以下情况+--+--+ | |a | | +--+ | b | | | +-----+
同时讲一个我在比赛时想到,但忘了函数名,现在查到的一个仅在Windows环境下对拍的方法:
链接:intersectRect 函数 (winuser.h) - Win32 apps | Microsoft Learn
intersectRect 函数 (winuser.h)
IntersectRect 函数计算两个源矩形的交集,并将交集矩形的坐标置于目标矩形中。 如果源矩形不相交,则 (将所有坐标设置为零的空矩形,) 放置在目标矩形中。
语法
BOOL IntersectRect( [out] LPRECT lprcDst, [in] const RECT *lprcSrc1, [in] const RECT *lprcSrc2 );参数
[out] lprcDst指向 RECT 结构的指针,用于接收 lprcSrc1 和 lprcSrc2 参数指向的矩形的交集。 此参数不能为 NULL。
[in] lprcSrc1指向包含第一个源矩形的 RECT 结构的指针。
[in] lprcSrc2指向包含第二个源矩形的 RECT 结构的指针。
返回值
如果矩形相交,则返回值为非零。
如果矩形不相交,则返回值为零。
注解
由于应用程序可以将矩形用于不同目的,因此矩形函数不使用显式度量单位。 相反,所有矩形坐标和维度都以有符号的逻辑值提供。 使用矩形的映射模式和函数确定度量单位。
示例
有关示例,请参阅 使用矩形。
注意,如果你调试,记得加上 #include <windows.h> ,同时提交时记得删掉。
#include <cstdio>
#define ll long long
ll n, ans;
ll fa[7010];
bool vis[7010];
struct RECT {
ll x1, y1, x2, y2;
} a[7010];
ll find(ll x) {
if(fa[x] == x) return fa[x];
return fa[x] = find(fa[x]);
}
bool check1(RECT a, RECT b) {
return (a.x1 <= b.x2 && b.x2 <= a.x2) || (a.x1 <= b.x1 && b.x1 <= a.x2);
}
bool check2(RECT a, RECT b) {
return (a.y1 <= b.y2 && b.y2 <= a.y2) || (a.y1 <= b.y1 && b.y1 <= a.y2);
}
bool inside(RECT a, RECT b) {
return (b.x1 <= a.x1 && a.x2 <= b.x2 && b.y1 <= a.y1 && a.x2 <= b.x2);
}
bool check3(RECT a, RECT b) {
return !(a.x1 == b.x2 && a.y1 == b.y2 && (inside(a, b) || !inside(b, a))) &&
!(a.x1 == b.x2 && b.y1 == a.y2 && (inside(a, b) || !inside(b, a)));
}
int main() {
freopen("pro.in", "r", stdin);
freopen("pro.out", "w", stdout);
scanf("%lld", &n);
for(ll i = 1; i <= n; i++) fa[i] = i;
for(ll i = 1; i <= n; i++) {
scanf("%lld %lld %lld %lld", &a[i].x1, &a[i].y1, &a[i].x2, &a[i].y2);
}
for(ll i = 1; i <= n; i++) {
for(ll j = i + 1; j <= n; j++) {
if((check1(a[i], a[j]) || check1(a[j], a[i])) && (check2(a[i], a[j]) || check2(a[j], a[i])) && (check3(a[i], a[j]) && check3(a[j], a[i]))) {
ll x = find(i);
ll y = find(j);
fa[x] = y;
}
}
}
for(ll i = 1; i <= n; i++) {
if(!vis[find(i)]) {
vis[fa[i]] = 1;
ans++;
}
}
printf("%lld", ans);
}
T2 平坦的折线(lam)
Description
现在我们在一张纸上有一个笛卡尔坐标系。我们考虑在这张纸上用铅笔从左到右画的折线。我们要求任何两个点之间连接的直线段与x轴的夹角在-45~45之间,一条满足以上条件的折线称之为平坦的折线。假定给出了n个不同的整点(坐标为整数的点),最少用几条平坦的折线可以覆盖所有的点?
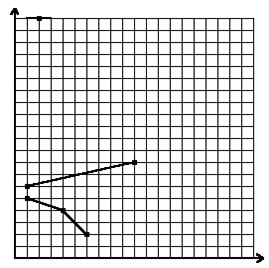
例子:
图中有6个整点:(1,6), (10,8), (1,5), (2,20), (4,4), (6,2),要覆盖它们至少要3条平坦的折线。任务:
写一个程序:
从文件lam.in中读入点的个数以及它们的坐标。
计算最少需要的折线个数。
将结果写入文件lam.out。Input
在输入文件lam.in的第一行有一个正整数n,不超过30000,代表点的个数。接下来的n行表示这些点的坐标,每行有两个用一个空格隔开的整数x,y,0 <= x <= 30000, 0 <= y <= 30000。第i+1行的数字代表第i个点的坐标。
Output
在输出文件lam.out的第一行应当有且仅有一个整数——表示覆盖所有的点最少需要的折线数。
Sample Input
6 1 6 10 8 1 5 2 20 4 4 6 2Sample Output
3Data Constraint
数据规模
对于20%的数据,有N<=15。
对于100%的数据如题目。
比赛时想到可以不用暴力旋转,只需要打一个平衡树(其实当时我想的是我最喜欢的权值线段树)然后找后继就行了,但是处理很麻烦,没打出来。
考虑整个图旋转45°,然后因为题目的要求,我们的折线现在只能严格递增。用f储存折线结尾的y坐标,然后从右到左跑一遍就行了。对于小于当前所有点的y坐标就新开折线,否则二分查找后继(或者平衡树)。
#include <cstdio>
#include <set>
#include <cmath>
#include <climits>
#define ll long long
using namespace std;
ll n;
struct POINT {
ll x, y;
friend bool operator> (const POINT &x, const POINT &y) {
if(x.x == y.x) return x.y < y.y;
return x.x > y.x; // 注意是从大到小排,具体原因自己想想吧QWQ
}
} a[30010], g[30010];
void solve(ll l, ll r) {
if(l == r) return;
ll mid = (l + r) >> 1;
solve(l, mid);
solve(mid + 1, r);
ll pos1 = l, pos2 = mid + 1;
for(ll i = l; i <= r; i++) {
if(pos2 > r || (pos1 <= mid && a[pos1] > a[pos2])) {
g[i] = a[pos1++];
} else {
g[i] = a[pos2++];
}
}
for(ll i = l; i <= r; i++) {
a[i] = g[i];
}
}
ll f[30010], ans;
int main() {
freopen("lam.in", "r", stdin);
freopen("lam.out", "w", stdout);
scanf("%lld", &n);
for(ll i = 1; i <= n; i++) {
ll x, y;
scanf("%lld %lld", &x, &y);
a[i].x = y - x;
a[i].y = y + x;
}
solve(1, n);
f[0] = INT_MAX;
for(ll i = 1; i <= n; i++) {
if(f[ans] > a[i].y) f[++ans] = a[i].y; // 要求单调递增,所以这里只能开新链了
else {
// 选一个最适合的ans来连接
ll l = 1, r = ans, res = 1;
while(l <= r) {
ll mid = (l + r) >> 1;
if(f[mid] <= a[i].y) {
res = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
f[res] = a[i].y;
}
}
printf("%lld", ans);
}
T3 Idiot 的间谍网络
Description
作为一名高级特工,Idiot 苦心经营多年,终于在敌国建立起一张共有n 名特工的庞大间谍网络。
当然,出于保密性的要求,间谍网络中的每名特工最多只会有一名直接领导。现在,Idiot 希望整理有关历次特别行动的一些信息。
初始时,间谍网络中的所有特工都没有直接领导。之后,共有m 次下列类型的事件按时间顺序依次发生:
• 事件类型1 x y:特工y 成为特工x 的直接领导。数据保证在此之前特工x 没有直接领导;
• 事件类型2 x:特工x 策划了一起特别行动,然后上报其直接领导审批,之后其直接领导再上报其直接领导的直接领导审批,以此类推,直到某个特工审批后不再有直接领导;
• 事件类型3 x y:询问特工x 是否直接策划或审批过第y 次特别行动。所有特别行动按发生时间的顺序从1 开始依次编号。数据保证在询问之前,第y 次特别行动已经发生过。
作为一名高级特工,Idiot 当然不会亲自办事。于是,Idiot 便安排你来完成这个任务。Input
第一行两个正整数n 和m,分别表示间谍网络中的特工总数,以及事件的总数。
接下来m 行,第i 行给出第i 个事件的信息,格式及含义参见题面。Output
输出共t 行,其中t 表示询问的总数。第i 行输出”Y ES” 或者”NO”,表示第i 次询问的答案。
Sample Input
6 12 2 1 1 4 1 3 4 1 1 3 4 2 3 3 4 1 2 3 3 4 2 3 1 1 3 1 3 3 1 2 1 2 4Sample Output
NO NO YES YES YES YESData Constraint
对于30% 的数据,n <= 3 10^3,m <= 5 10^3;
对于60% 的数据,n <=2 * 10^5,m <= 2 * 10^5;
额外20% 的数据,保证在任意时刻,整张间谍网络由若干条互不相交的链构成;
对于100% 的数据,n <= 5 * 10^5,m <= 5 * 10^5;
C + + 选手的程序在评测时使用编译选项-Wl;--stack = 104857600。
考试时看到这道题想的是离线,然后打了个暴力离线加优化。
结果真的是离线。
题目要求我们实现:
- 设置 \(x\) 为 \(y\) 的祖先
- 将 \(x\) 及其祖先打上标记
- 判断在某一时刻 \(x\) 是否有 \(y\) 的标记。
我们稍微转换操作 3. ,可以先把查询储存下来,遍历我们的操作 2. 的行动编号 ,如果刚好有对操作 2. 的查询,那么我们就在进行完操作 2. 后(因为题目保证在询问之前,第 y 次特别行动已经发生过。),查询 \(x\) 是否为行动 \(y\) 的发起者的祖先,这样就可以去掉 某一时刻 这个条件。
那么怎么判断 \(x\) 是 \(y\) 的祖先呢?
说到祖先,我们总可以想到并查集。
那么我们只需要查询两人的祖先即可……吗?
非也,因为可能为这样,在这里,x与y的祖先虽然相同,可是却是y是x的祖先:
那么我们就可以判断两人的深度……吗?
非也,因为可能为这样,在这里,x与y的祖先虽然相同,x与y无关系:
那么应该怎么办呢?这时,时间戳就派上用场了。
当我们在遍历一个节点的子树前,我们先要添加一个 \(st\) 时间戳为 ++ti 。
当我们在遍历完一个节点的子树后,我们先要添加一个 \(ed\) 时间戳为 ++ti 。
那么这样,但凡时间戳在 \([st, ed]\) 内的都是这个节点的子树。
所以我们在判祖先相同的同时还要判时间戳在 \([st, ed]\) 内。
#include <cstdio>
#include <algorithm>
#define ll long long
using namespace std;
ll n, m;
/* 离线操作 */
struct QUERY {
ll op, x, y, id;
} query[500010], e[500010], a[500010], d[500010];
ll ecnt, acnt, dcnt;
/* 冰茶几 */
ll fa[500010];
ll find(ll x) {
if(fa[x] == x) {
return x;
}
return fa[x] = find(fa[x]);
}
void merge(ll x, ll y) {
x = find(x);
y = find(y);
fa[x] = y;
}
/* 前向星 */
ll head[500010];
ll nxt[500010];
ll to[500010], cnt;
void addEdge(ll u, ll v) {
++cnt;
to[cnt] = v;
nxt[cnt] = head[u];
head[u] = cnt;
}
/* 记录时间戳 */
ll st[500010], ed[500010];
bool vis[500010];
ll ti;
/* 生成dfn */
void dfs(ll u) {
ti++;
vis[u] = true;
st[u] = ti;
for(ll i = head[u]; i; i = nxt[i]) if(!vis[to[i]]){
ll v = to[i];
dfs(v);
}
ed[u] = ti;
}
bool ans[500010];
bool cmp(QUERY x, QUERY y) {
return x.y < y.y;
}
int main() {
scanf("%lld %lld", &n, &m);
for(ll i = 1; i <= n; i++) fa[i] = i;
for(ll i = 1; i <= m; i++) {
query[i].id = i;
scanf("%lld", &query[i].op);
switch(query[i].op) {
case 1:
scanf("%lld %lld", &query[i].x, &query[i].y);
addEdge(query[i].y, query[i].x);
merge(query[i].x, query[i].y);
e[++ecnt] = query[i];
break;
case 2:
scanf("%lld", &query[i].x);
d[++dcnt] = query[i];
break;
case 3:
scanf("%lld %lld", &query[i].x, &query[i].y);
a[++acnt] = query[i];
break;
}
}
for(ll i = 1; i <= n; i++) {
ll u = find(i);
if(!vis[u]) {
dfs(u);
}
}
for(ll i = 1; i <= n; i++) fa[i] = i; // 清空并查集,防止出现后来的上级误以为审批的情况
sort(a + 1, a + 1 + acnt, cmp); // 按照查询的时间顺序进行排序
ll ei = 1, ai = 1;
for(ll di = 1; di <= dcnt; di++) { // 枚举特别行动
for(; e[ei].id <= d[di].id; ei++) merge(e[ei].x, e[ei].y); // 把上一次的发起行动,到这一次的发起行动,之间的认爹全部跑一遍
for(; a[ai].y == di; ai++) { // 看有没有查询这次发起行动的
ll u = find(a[ai].x); // 找父亲
ll v = find(d[di].x);
if(u == v && // 判断祖先相同,并且
st[a[ai].x] <= st[d[di].x] && st[d[di].x] <= ed[a[ai].x]) { // 这次发起行动在x的子树间
ans[a[ai].id] = 1;
}
}
}
for(ll i = 1; i <= m; i++) {
if(query[i].op == 3)
printf("%s\n", ans[i] ? "YES" : "NO");
}
}
T4 Idiot 的乘幂
Description
Input
第一行一个正整数t,表示测试数据组数。
接下来t 行,每行五个正整数a、b、c、d、p,表示一组测试数据。Output
一共t 行,第i 行表示第i 组测试数据的答案。若该组测试数据无解,则输出No Solution!,否则输出一个正整数x(1 <= x < p),表示同余方程组的解。
Sample Input
10 22 1 3 17 24 6 12 5 6 13 16 16 9 1 19 11 1 14 2 23 8 4 17 15 19 10 3 9 1 13 11 1 2 2 23 13 2 14 12 17 11 9 7 11 14 15 10 7 7 17Sample Output
17 2 5 16 14 3 18 No Solution! 11 12Data Constraint
暴力,寄。
然后结束后后知后觉,看题目那么多gcd,那肯定得考虑exgcd呀。
把题目中的方程组组合在一起就变成了:
然后我们假定两个数\(x,y\)使得:
那么显然:
所以
那我们就可以根据 \(ax+cy=1\) 跑一遍exgcd,再根据 \(X\equiv b^x\cdot d^y(\mod p)\),就能得出 \(X\) 了。
\(x\) 可能为负数,如果它们为负数,那么它就相当于 \(\frac{1}{b^{-x}}=b^{-1^{-x}}\)
\(y\) 同上。所以如果它们小于0记得还要求个逆元。
#include <cstdio>
#define ll long long
ll t, a, b, c, d, p, x, y;
ll qpow(ll n, ll q) {
if(q == 0) return 1;
if(q % 2 == 0) {
ll res = qpow(n, q / 2);
return res * res % p;
}
return qpow(n, q - 1) * n % p;
}
ll exgcd(ll a, ll b) {
if(b == 0) {
x = 1, y = 0;
return a;
}
ll r = exgcd(b, a % b);
ll t = x;
x = y;
y = t - (a/b) * y;
return r;
}
int main() {
scanf("%lld", &t);
while(t--) {
scanf("%lld %lld %lld %lld %lld", &a, &b, &c, &d, &p);
exgcd(a, c);
ll l, r;
ll tmpx = x, tmpy = y;
if(tmpx >= 0) {
l = qpow(b, tmpx);
} else {
exgcd(b, p);
x = (x % p + p) % p;
l = qpow(x, -tmpx);
}
if(tmpy >= 0) {
r = qpow(d, tmpy);
} else {
exgcd(d, p);
x = (x % p + p) % p;
r = qpow(x, -tmpy);
}
if(qpow(l * r % p, a) == b % p && qpow(l * r % p, c) == d % p) {
printf("%lld\n", l * r % p);
} else {
printf("No Solution!\n");
}
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号