20230814 总结
T1 简单题(simple)
Description
dzy 手上有一张n 个点m 条边的联通无向图,仙人掌是一张每条边最多在一个简单环内的联通无向图。他想求这个无向图的生成仙人掌中最多有多少条边。
但是dzy 觉得这个问题太简单了,于是他定义了“美丽的生成仙人掌”,即在一个生成仙人掌中如果满足对于任意编号为i,j(i < j) 的两点,存在一条它们之间的简单路径上面有j-i+1 个点,则这个仙人掌是美丽的。
他现在想要知道这张图的美丽的生成仙人掌中最多有多少条边,你能帮帮他吗?Input
第一行两个整数n,m。接下来m 行每行两个整数ui,vi,表示这两个点之间有一条无向边。保证图中没有自环。
Output
仅一行一个整数表示答案。
Sample Input
2 1 1 2 Sample Output
1 Data Constraint
对于10% 的数据,n <=10。
对于30% 的数据,n <=10^3。
对于100% 的数据,n <=10^5,m <= 2n。
题目大意:给定联通无向图,求满足以下条件的边数量:
- 每条边最多在一个简单环内(也就是环,当时愣了很久,于是就没打出来)
- 对于任意编号为 \(i,j(i < j)\) 的两点,存在一条它们之间的简单路径上面有 \(j-i+1\) 个点
首先我们可以发现,条件2很好求,就是肯定有一条从1到n的链。长这样:
为什么,因为根据条件2,任意编号为 \(i,i + 1\) 的两点,存在一条它们之间的简单路径上面有 \(2\) 个点。那么 \(i,i + 1\) 间肯定有一条边直接相连,满足了这条性质,其它的 \(i,j\) 就必定满足。
因为如果 \(i,j\) 满足了这条性质,那么 \(i,j+1\) 必定满足,根据数学归纳法,其它的必定满足。
如果这道题要求求最少边的话,我们已经做完了。
可是题目要求求最多的边,那么……
就加嘛!
我们就直接加,这里很容易可以得到一个DP:
其中 \(j\) 是与 \(i\) 直接相连的边,且 \(i_{右端点} > j_{右端点}\) 。
为什么它可以保证条件1呢?因为我们看按右端点排序后是什么样的:
当我们在 \(i = 7,j=4\) 的时候,因为 4 之前的右端点绝对小于 4,所以在 $ [4, 7]$ 这段区间内不可能出现,不会与 \([4,7]\) 交叉。
所以我们枚举 \(i,j\) 即可?非也,这么做复杂度为 \(n^2\) ,因为 f 数组必定是递增的,所以说取右边的一定比取左边的优。那么我们只需要在输入时预处理一个点距离它最近在它左边的那一个点 \(j\) 。
总结就是想复杂了,同时图论看少了(竟然不知道简单环QWQ)
#include <cstdio> #include <algorithm> #define ll long long using namespace std; ll n, m; ll u, v; ll g[100010]; ll f[100010]; int main() { scanf("%lld %lld", &n, &m); for(ll i = 1; i <= m; i++) { scanf("%lld %lld", &u, &v); if(u > v) swap(u, v); if(u < v - 1 && g[v] < u) g[v] = u; } for(ll i = 1; i <= n; i++) { if(g[i]) { f[i] = max(f[i - 1], f[g[i]] + 1); } else { f[i] = f[i - 1]; } } printf("%lld", f[n] + n - 1); }
T2 困难的图论
Description
给定由 n 个点 m 条边组成的无向连通图,保证没有重边和自环。
你需要找出所有边,满足这些边恰好存在于一个简单环中。一个环被称为简单环,当且仅当它包含的所有点都只在这个环中被经过了一次。
注意到这些边可能有很多条,你只需要输出他们编号的异或和即可。Input
第一行两个数 n, m。
接下来 m 行,每行两个数 ai , bi,表示第 i 条边连接了 ai , bi。Output
输出一个数,表示所有满足条件的边的编号的异或和。
Sample Input
Sample Input1 4 4 1 2 2 4 4 3 3 2 Sample Input2 4 5 1 2 1 3 2 4 4 3 3 2 Sample Output
Sample Output2 5 Sample Output2 0 对于第一个样例,2,3,4 满足要求。 对于第二个样例,所有边都不满足要求。 Data Constraint
比赛时看了又看,看了又看,总结出:
这不就是割点嘛!
我们定义一个”美丽的区间“为这样(我不知道怎么描述):
然后我们发现,对于美丽的区间C这种不是简单环的区间,最终一定是每条边可以在多个环中。
对于美丽的区间A、B这种是简单环的区间,最终一定是每条边都只在一个环中。
对于中间这种割点,它们组成的边是不属于任意一个简单环的,所以最终一定是每条边不属于任意一个简单环。
那么就好办了,用某一个神奇的算法求出这些“美丽的区间”,然后判是不是简单环即可。
Q:可是,怎么求“美丽的区间”呢?
A:当然是割点啦!
Q:割点怎么求?
A:当然是Tarjan啦(记得讲过)
Q:我忘了。
好了,然后就打了个暴力拿了 30pts。
故事讲完了,比赛时想到的神奇算法叫:点双连通分量。
这个因为篇幅有限,不讲这些算法了。
然后怎么判简单环,很简单,我们计算出一个“美丽的区间”的点数和边数,如果它们相等说明这是简单环,边数大于点数说明这不是简单环。边数小于点数说明这是一条链。
然后就是困扰了我很久的问题:怎么求边数。
点数很容易,因为我们在记录 栈 的时候就是存的点嘛,这样我们才能知道哪些是割点或者割边。边数的算法则是我从来没遇到的。
其实这是一个特例,我以前学的 Tarjan 算法都是记录点的,那么我们在记录 栈 的时候存边不久行了嘛,因为记录边可以带上左右端点,然后拿个 vis 判重不就行了?
然后就是(这题细节真多)vis的重置,刚开始用 memset 重置是会 T 的,但是我改变了一种方式,就是不重置,添加 id ,memset(vis, 0, sizeof(vis)) 就是 id ++ ,vis = true 就是 vis = id ,vis == true 就是 vis == id。
就没有然后了。
// 我选择,手写栈 #include <cstdio> #include <climits> #include <ctime> #define N 2000010 int n, m, ans; /* =====================minmax===================== */ inline int min(int x, int y) { return x > y ? y : x; } inline int max(int x, int y) { return x < y ? y : x; } /* ====================边结构体==================== */ struct node { int id, u, v; }; /* =======================栈======================= */ class stack { private: node st[N]; int stackTop = 0; public: inline void pop() { stackTop--; } inline void push(node x) { st[++stackTop] = x; } inline node top() { return st[stackTop]; } inline int size() { return stackTop; } }; /* ===================vis class=================== */ class vis { private: int visId = 0; int v[N]; public: inline void clear() { visId++; } inline void setVis(int x) { v[x] = visId; } inline bool getVis(int x) { return v[x] == visId; } }; /* =====================前向星===================== */ int head[N]; int nxt[N]; int to[N]; int id[N]; int cnt; inline void addEdge(int u, int v, int num) { ++cnt; to[cnt] = v; id[cnt] = num; nxt[cnt] = head[u]; head[u] = cnt; } /* ====================tarjan==================== */ int dfn[N], low[N]; int tot; bool cut[N]; stack side; vis used; void tarjan(int u, int rt, int fa) { dfn[u] = low[u] = ++tot; for(int i = head[u]; i; i = nxt[i]) { int v = to[i]; int nowTop = side.size(); if(v != fa && dfn[v] < dfn[u]) { side.push((node){id[i], u, v}); } if(!dfn[v]) { tarjan(v, rt, u); // 跑下去 low[u] = min(low[u], low[v]); if(low[v] >= dfn[u]) { cut[u] = true; int point_tot = 0, side_tot = 0; int res = 0; used.clear(); while(side.size() > nowTop) { node x = side.top(); side.pop(); side_tot++; res ^= x.id; if(!used.getVis(x.u)) { point_tot++; used.setVis(x.u); } if(!used.getVis(x.v)) { point_tot++; used.setVis(x.v); } } if(point_tot == side_tot) { ans ^= res; } } } else if(v != fa) { low[u] = min(low[u], dfn[v]); } } } /* ====================快读==================== */ int read() { int x = 0; char c = '.'; while (c < '0' || c > '9') c = getchar(); while (c >= '0' && c <= '9') { x = (x << 1) + (x << 3) + (c ^ '0'); c = getchar(); } return x; } int main() { freopen("graph.in", "r", stdin); freopen("graph.out", "w", stdout); n = read(), m = read(); int u, v; for(int i = 1; i <= m; i++) { u = read(), v = read(); addEdge(u, v, i); addEdge(v, u, i); } tarjan(1, 1, 1); // 这是个连通图,跑一遍就够了 printf("%d", ans); }
T3 随机关卡(game)
Description
“德克萨斯那家伙能活得那么潇洒,可多亏了有我罩着她,这不是明摆着的事情嘛”
Texas 和 Exusiai 两个人正在玩一个游戏,游戏有 n 种不同的关卡可以挑战, 每次挑战需要消耗 1 点理智。
对于关卡 i (1 ≤ i ≤ n) ,每个人都有相同的概率 pi成功完成任务并获得 1 点 积分,有 1-pi的概率行动失败不能获得任何奖励。
Texas 和 Exusiai 的策略是使用所有理智每次等概率随机一个关卡挑战。现在 Texas 有 A 点理智,Exusiai 有 B 点理智,Exusiai 想知道在两人的所有理智用完之后,Exusiai 的积分严格大于 Texas 的概率模 10000019 意义下的值。Input
第一行三个数 n, A, B。
第二行共 n 个数,第 i 数为 pi 。Output
一个数,表示 Exusiai 的积分严格大于 Texas 的概率模 10000019 意义下的值。
Sample Input
2 1 1 5000010 5000010 Sample Output
2500005 Data Constraint
对于全部的数据,1 ≤ n, A ≤ 5×10^6, 1 ≤ B ≤ 10^18 , 0 ≤ pi< 100000019 。
子任务规模描述如下:
- 子任务1(10分):1 ≤ n, A, B ≤ 10
- 子任务2(10分):1 ≤ n, A, B ≤ 10^3,依赖子任务1。
- 子任务3(10分):1 ≤ A ≤ 100,依赖子任务1。
- 子任务4(30分):1 ≤ B ≤ 2 × 10^6,依赖子任务2。
- 子任务5(40分):无任何特殊限制,依赖子任务3,4。
对于一个子任务,通过该子任务必须通过该子任务的所有测试数据以及其依赖的子任务。
Hint
【样例解释】
最终答案是 1/4。【提示】
数据的读入量可能较大,你可以选择使用并不下发的读入优化。
该题的概率都以整数的形式给出,该整数在模题目指定模数意义下可以写成 P × Q^−1 的形式。
比赛时完全不会。
结束时看到了这个:
该整数在模题目指定模数意义下可以写成 \(P × Q^{−1}\) 的形式。
emm……还是不会。
结束时才发现这么简单!!!
我们知道,在某一个游戏赢一场的概率是:
选择到某一个游戏的概率是:
那么选择到某一个游戏并且赢一场的概率是:
那么赢一场的概率是:
同理,那么输一场的概率是:
继续。我们知道,在 \(n\) 次游戏里选择 \(m\)次的情况数有:
在 \(n\) 次游戏里选择 \(m\) 次赢且这些次游戏都赢了的概率有:
那么在 \(n\) 次游戏里选择 \(m\) 次赢且这些次游戏都赢了且其他次游戏都输了的概率有:
也就是说,在 \(n\) 次游戏里只赢 \(m\) 次的概率为:
因为一次理智相当于一次游戏。那么很快我们就可以得到一个数列 \(a_i\),表示在 \(A\) 次游戏中只赢了 \(i\) 次游戏的概率,即只有 \(i\) 个理智发挥作用的概率。
可是这么求是会超时的,让我们递推吧!
首先,因为:
所以:
这就是组合的递推式,然后剩下两个就很好搞了:
(PS:上面说的 -1 次方都是逆元)
总的来说就是:
逆元使用线性求逆元。
具体百度优先搜索。
0初始值是 \((P_{lose})^A\) ,请感性理解,或者继续看下去
然后呢?又挂了。
下载数据点发现是这样的:
10 9 8 1 1 1 1 1 1 1 1 1 1
为什么会错呢,主要是因为一个数学和编程的差别,在这里, \(P_{lose}\) 是0,当 \(i = A \text{ or } B\) 时,会出现 \(0^0\)。(不是递推式,是原式 \(a_i = C^i_A\cdot(P_{win})^i\cdot(P_{lose})^{A-i}\))
在数学上,\(0^0\) 是不存在的,但是我现在有两种解释:
- 因为当 \(i = A \text{ or } B\) ,我们是不会考虑 \((P_{lose})^{A-i}\) 的,因为 \(i = A \text{ or } B\) 意味着没有失败,这时我们只考虑成功,为了使它不会变成0,我们定义 \(0^0=1\) 。
- 在概率论中,空事件是指不会发生的事件,概率为0。在这种情况下,0的0次方定义为1,以便保持一些概率公式的一致性和简洁性。
所以这就可以结社为什么会错。我们就要特判几个特殊的 \(i\) 。
-
\(i = 0\),这时 \((P_{win})^i\) 就可能会出现 \(0^0\) ,我们就可以使用以下公式计算
\[a_0\text{ or } b_0=C^0_A\cdot1\cdot(P_{lose})^{A-0}=(P_{lose})^A \]这同时解释了上面的初始值问题。
-
\(i = A \text{ or } B\),这时 \((P_{lose})^i\) 就可能会出现 \(0^0\) ,我们就可以使用以下公式计算
\[a_A\text{ or } b_B=1\cdot(P_{lose})^{A\text{ or }B}\cdot1=(P_{lose})^{A\text{ or }B} \]
接下来怎么做呢?很简单,因为要判 Exusiai(b) 的积分严格大于 Texas(a) ,所以我们就是求:
这个感性理解?但是,因为 \(1 ≤ A ≤ 5×10^6, 1 ≤ B ≤ 10^{18}\) ,如果遍历一遍B就会T,所以我们把题目改一改,改成 Texas(a) 的积分大于等于 Exusiai(b) 的概率,这样就很好求吧:
\(b_j\) 可用前缀和 \(sum\) 维护。
因为我们改了题目,所以得出来得结果相反,需要用1减去:
注意需要随地大小模!建议使用 模数类。
以及,快速读入不行,还要 fread!!
#include <cstdio> #include <cmath> #include <algorithm> #include <ctime> #define moder(x) (((x) % P + P) % P) using namespace std; #define ll long long const ll P = 10000019; ll qpow(ll n, ll p) { if(p == 0) return 1; if(p % 2 == 0) { ll res = qpow(n, p / 2) % P; return res * res % P; } return ((qpow(n, p - 1) % P) * (n % P)) % P; } struct ModLL { ll val; friend ModLL operator +(const ModLL &x, const ModLL &y) {return (ModLL){moder(moder(x.val) + moder(y.val))};} friend ModLL operator -(const ModLL &x, const ModLL &y) {return (ModLL){moder(moder(x.val) - moder(y.val))};} friend ModLL operator *(const ModLL &x, const ModLL &y) {return (ModLL){moder(moder(x.val) * moder(y.val))};} friend ModLL operator /(const ModLL &x, const ModLL &y) {return (ModLL){moder(moder(x.val) * qpow(y.val, P - 2))};} // 最后这个比较特殊,乘以它的逆元 ModLL& operator =(const ModLL &x) {val = moder(x.val);return *this;} ModLL& operator =(const ll &x) {val = moder(x);return *this;} operator ll() const {return val;} }; inline char get() { static char buf[100000], *p1 = buf, *p2 = buf; return p1 == p2 && (p2 = (p1 = buf) + fread(buf,1,100000,stdin),p1 == p2) ? EOF : *p1 ++; } ll read() { ll x = 0; char c = '.'; while(c < '0' || c > '9') c = get(); while(c >= '0' && c <= '9') { x = (x << 1) + (x << 3) + (c ^ '0'); c = get(); } return x; } ModLL n, A, B; ModLL p[5000010]; ModLL a[5000010]; ModLL b[5000010]; ModLL s[5000010]; ModLL inv[5000010]; ModLL ans; ModLL sum1; ModLL sum2; ModLL sum2inv; ModLL ninv; ModLL sum1A = (ModLL){1}, sum1B = (ModLL){1}; void getInv() { inv[1] = 1; for(ll i = 2; i <= A; i++) { inv[i] = (P - P / i) * inv[P % i]; } } int main() { freopen("game.in", "r", stdin); freopen("game.out", "w", stdout); n.val = read(); A.val = read(); B.val = read(); for(ll i = 1; i <= n; i++) { p[i].val = read(); sum1 = sum1 + p[i]; sum2 = sum2 + (1 - p[i]); } getInv(); ninv = qpow(n, P - 2); sum1 = sum1 / n; sum2 = sum2 / n; a[0] = qpow(sum2, A); b[0] = qpow(sum2, B); sum2inv = qpow(sum2, P - 2); for(ll i = 1; i <= A; i++) { a[i] = a[i - 1] * (ModLL){(A - i + 1)} * inv[i] * sum1 * sum2inv; if(i <= A) sum1A = sum1A * sum1; if(i <= B) sum1B = sum1B * sum1; if(i <= B) { b[i] = b[i - 1] * (ModLL){(B - i + 1)} * inv[i] * sum1 * sum2inv; } } // 由于数学上不存在0^0,可在这里是成立的,0^0=1 if(sum2 == 0) { a[A] = 1 * sum1A * 1; if(B <= A) { b[B] = 1 * sum1B * 1; } } // 前缀和 s[0] = b[0]; for(ll i = 1; i <= A; i++) { s[i] = s[i - 1] + b[i]; } // 计算答案 for(ll i = 0; i <= A; i++) { ans = ans + a[i] * s[i]; } ans = (ModLL){1} - ans; printf("%lld", ans); }
T4 上网
Description
小L做题做累了,他决定上网放松一下。于是小L打开了一款网游,这款网游的名字叫做PION,是一个休闲养生的益智游戏,小L玩得不亦乐乎。
这天小L在做主线剧情的时候,又遇到了一个困难的任务:攻破P城的城墙!小L仔细观察,发现城墙上一共有 \(n\) 个士兵排成一行,每个士兵都有一个防守值 \(a_i\) 。要想攻破城墙,就必须详细的了解每一个士兵的防守值。不过不幸的是,在小L只观察完了一部分士兵后,家里的网突然断了!
小L只记得士兵的防守值是位于 \([1,10^9]\)之间的整数,此外,他还记得一些士兵的防守值,以及在某些区间段 \([L_i,R_i]\) 中,防守值最高的士兵是哪几个。小L并不想浪费时间,于是他把这些信息告诉了你,想让你告诉他一组士兵可能的防守值,以便于他连上网络后立刻发动进攻。
Input
第一行包含三个正整数n,s,m。
接下来s行,每行包含两个正整数 pi,di,表示已知 \(a_{p_i}=d_i\),保证pi递增。
接下来m行,每行一开始为三个正整数li,ri,ki,接下来ki个正整数x1,x2,xk(\(l_i\le x_1<x_2<\cdots<x_{k_i}\le r_i\)),表示这ki个数中的任意一个都比任意一个剩下的\(r_i-l_i+1-k_i\)个数大(严格大于)。
Output
若无解,则输出”Impossible”。
否则第一行输出”Possible”,第二行输出 n 个正整数,依次输出序列 a 中每个数。Sample Input
5 2 2 2 7 5 3 1 4 2 2 3 4 5 1 4 Sample Output
Possible 6 7 1000000000 6 3 Data Constraint
对于30%的数据,\(n \le 1000\)。
对于70%的数据,\(n \le 50000\)。
对于100%的数据,$n \le 10^{5} ,m \le 2\times 10^{5} , \sum_{i} k_{i} \le 3\times 10^{5} $
第一眼——这不就是 拓扑 嘛!
然后就被题目数据大小秒杀了。
其实我们只需要优化:
优化 1 :
1. 对于每个 \(k_i\) ,新建一个超级点 \(t\) ,把 \(x_1∼x_{k_i}\) 连接 \(t\) ,边权设为 0
2. 再把 \(t\) 连接除 \(x_1∼x_{k_i}\) 外 \(l∼r\) 的点,边权设为 1
这样便只有 \(O(\sum_{i=1}^m r_i-l_i+1)\) 条边
也就是:
优化 2 :
我们可以建一棵线段树,每个点表示此区间的最大值。然后所有儿子连上它的父亲(因为儿子没走完,父亲就有入度,这样就可以保证父亲不会比儿子先更新,一定会先更新小区间),共 \(O(n\log n)\) 条边。我们发现 : 优化 1 的 1. 只连了 \(O(\sum k_i)\) 条边,但是优化 1 的 2. 连了 \(O(\sum_{i=1}^m r_i-l_i+1 - k_i)\) 条。
故我们可以沿用优化 1 的 1. ,改进 2.
我们发现,\(l∼r\) 被 \(x_1~x_{k_i}\) 分成了几份,每份的点是连续的(我们认为只有一个点也算连续)。我们可以让超级点 \(t\) 连接这 几 个区间在线段树的位置( 可能 1 个区间会被分成多块 )
这样就只连了 \(O(k\log n)\) 条边,然后就可以跑拓扑了。
#include <cstdio> #include <queue> using namespace std; #define N 6000010 #define ls(x) ((x) << 1) #define rs(x) ((x) << 1 | 1) int n, s, m, node; int val[N]; int ans[N]; int id[N]; int rd[N]; // 入度 int to[N]; int head[N]; int nxt[N]; int cost[N], cnt; int f[N]; int x[N]; inline int max(int x, int y) { return x > y ? x : y; } void addEdge(int u, int v, int k) { rd[v]++; ++cnt; to[cnt] = v; cost[cnt] = k; nxt[cnt] = head[u]; head[u] = cnt; } void build(int l, int r, int pos) { if(l == r) { id[pos] = l; return; } id[pos] = ++node; int mid = (l + r) >> 1; build(l, mid, ls(pos)); build(mid + 1, r, rs(pos)); addEdge(id[ls(pos)], id[pos], 0); addEdge(id[rs(pos)], id[pos], 0); } void update(int nl, int nr, int l, int r, int pos, int k) { if(nl <= l && r <= nr) { addEdge(id[pos], k, 1); return; } int mid = (l + r) >> 1; if(nl <= mid) update(nl, nr, l, mid, ls(pos), k); if(mid < nr) update(nl, nr, mid + 1, r, rs(pos), k); } bool chk() { int tot = 0; queue<int> q; for(int i = 1; i <= node; i++) if(!rd[i]) q.push(i); while(!q.empty()) { tot++; int u = q.front(); q.pop(); if(ans[u] > 1e9) return false; if(val[u] && ans[u] > val[u]) return false; ans[u] = max(1, max(ans[u], val[u])); for(int i = head[u]; i; i = nxt[i]) { int v = to[i]; ans[v] = max(ans[v], ans[u] + cost[i]); rd[v]--; if(rd[v] == 0) q.push(v); } } return tot >= node; } int read() { int x = 0; char c = '.'; while (c < '0' || c > '9') c = getchar(); while (c >= '0' && c <= '9') { x = (x << 1) + (x << 3) + (c ^ '0'); c = getchar(); } return x; } int main() { freopen("web.in", "r", stdin); freopen("web.out", "w", stdout); n = read(), s = read(), m = read(); node = n; for(int i = 1; i <= s; i++) { int p = read(), d = read(); val[p] = d; } build(1, n, 1); for(int i = 1; i <= m; i++) { int l, r, k; l = read(), r = read(), k = read(); int fake = ++node; x[0] = l - 1; x[k + 1] = r + 1; for(int j = 1; j <= k; j++) { x[j] = read(); addEdge(fake, x[j], 0); } for(int j = 1; j <= k + 1; j++) { if(x[j - 1] + 1 <= x[j] - 1) update(x[j - 1] + 1, x[j] - 1, 1, n, 1, fake); } } if(chk()) { printf("Possible\n"); for(int i = 1; i <= n; i++) { printf("%d ", ans[i]); } } else { printf("Impossible"); } }

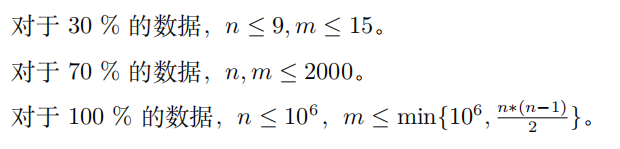


· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 按钮权限的设计及实现