2）最短路径应用
路径拟合：
1. 准备数据
门架点集合、门架点连通关系、任意连通的门架点之间最短路径（通过最短路径算法，基于门架连通关系数据计算得出）
2. 入参
有序的门架点数组
3. 计算
a. 初始化连通关系数据
b. 初始化最短路径数据
c. 将入参数组按照相邻点，两两分组，分别验证连通性。若某组两点具备连通性，则最短路径由这两点组成；若某组两点不具备连通性，则查询最短路径数据，获得这两点的最短路径。若所有分组均具有连通性，则该条线路正常。如果出现一组或多组数据不具备连通性，则该线路异常。
d. 所有分组数据验证完毕后，将所有组的最短路径整合为一条完整路径
4. 返回
返回得到的完整路径，并用于后续费用计算
路径拟合示例：
1. 准备数据
a 门架点 a,b,c,d,e,f,g,h
b 连通关系
a->c,47
a->e,70
a->f,24
b->d,31
b->g,74
b->h,79
c->b,55
c->d,88
c->g,66
c->e,23
d->h,29
e->g,42
e->b,31
f->c,25
f->d,120
g>h,66
c. 最短路径
a:f=a,f(24)
a:c=a,c(47)
a:e=a,e(70)
a:b=a,e,b(101)
a:g=a,e,g(112)
a:d=a,e,b,d(132)
a:h=a,e,b,d,h(161)
b:d=b,d(31)
b:h=b,d,h(60)
b:g=b,g(74)
c:e=c,e(23)
c:b=c,e,b(54)
c:g=c,e,g(65)
c:d=c,e,b,d(85)
c:h=c,e,b,d,h(114)
d:h=d,h(29)
e:b=e,b(31)
e:g=e,g(42)
e:d=e,b,d(62)
e:h=e,b,d,h(91)
f:c=f,c(25)
f:e=f,c,e(48)
f:b=f,c,e,b(79)
f:g=f,c,e,g(90)
f:d=f,c,e,b,d(110)
f:h=f,c,e,b,d,h(139)
g:h=g,h(66)
最短路径计算方法:
1基于所有点生成邻接矩阵，当两点之间不直接连通时用正无穷 ∞ 表示：
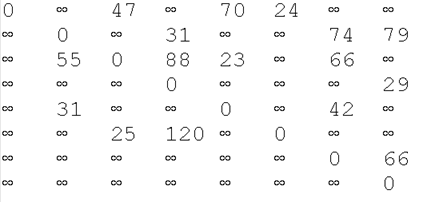
2 选则一个root 节点 ，比如 a
3 初始化两个集合 A 和B 。集合A中存放已检查点，集合B中存放待检查点
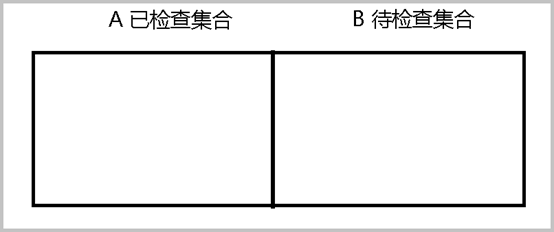
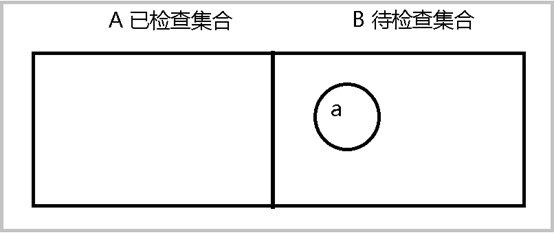
4 将a 设置为待检查点并放入集合B中
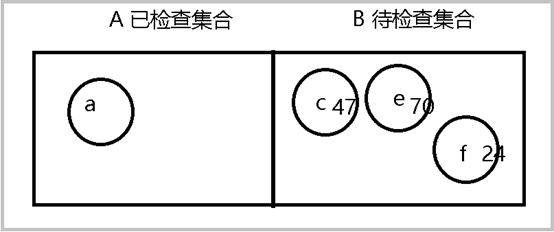
5 在临接矩阵中搜索 a 的连通点，不包含a本身和已经放置到已检查集合A中的点。本次搜出 c , e, f ，将这3点放入待检查集合B中，然后将a 转移至 已检查集合A中。
6 点c 距离 a长度47 ， 点e 距离 a 长度 70 ，点f 距离a 长度 24 ，选举出距离a点最短的点 f ，查找f 的连通点。本次搜出 d,c （d直接放，c需要比较），如果集合B中已经存在新搜出的点，需要比较新搜出的点和已存在的点哪个距离root点最短，将最短的点更新到集合B。本次B中已存在c ,路径c49(a->f->c), 大于c47(a->c),取c47。
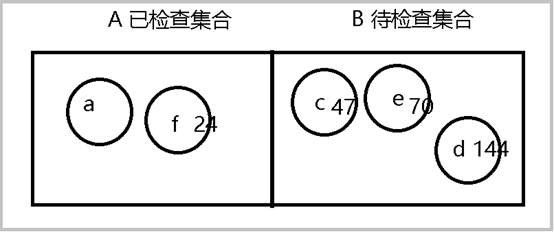
7 从B中选举最短路径点c , 重复上述步骤，直到B集合不再产生新的点。
8 上述步骤结束，已经计算出距离a 最近的所有点。还需将 root 替换为 b, c, d … 计算出所有点之间的最短路径数据，以供查询。
2. 入参（2组）
a,f,h
a,e,b,d,h
3. 计算
a. 初始化连通关系数据
{
"a": ["c","e","f"],
"b": ["d","g","h"],
"c": ["b","d","e","g"],
"d": ["h"],
"e": ["b","g"],
"f": ["c","d"],
"g": ["h"]
}
b. 初始化最短路径数据
{
"a:b": "a,e,b",
"a:d": "a,e,b,d",
"c:b": "c,e,b",
"a:c": "a,c",
"a:f": "a,f",
"c:d": "c,e,b,d",
"e:b": "e,b",
"a:e": "a,e",
"b:d": "b,d",
"a:h": "a,e,b,d,h",
"b:g": "b,g",
"e:d": "e,b,d",
"f:c": "f,c",
"a:g": "a,e,g",
"c:e": "c,e",
"f:b": "f,c,e,b",
"c:h": "c,e,b,d,h",
"f:e": "f,c,e",
"b:h": "b,d,h",
"c:g": "c,e,g",
"f:d": "f,c,e,b,d",
"e:h": "e,b,d,h",
"f:g": "f,c,e,g",
"d:h": "d,h",
"e:g": "e,g",
"g:h": "g,h",
"f:h": "f,c,e,b,d,h"
}
c. 计算
|
入参 |
分组 |
各组验证 |
各组最短路径 |
完整路径 |
|
a,f,h |
a,f ; f,h |
true,false |
[a,f] ,[f,c,e,b,d,h] |
a,f,c,e,b,d,h |
|
a,e,b,d,h |
a,e; e,b; b,d ; d,h |
true,true,true,true |
[a,e],[e,b],[b,d],[d,h] |
a,e,b,d,h |
①相邻点两两分组。
②验证各组连通性，举例验证a,f 连通性，通过key “a” 查询连通关系数据,如果查到数据，且该数据集中包含”f” ，则具备连通性。
③若某组不具备连通性，则查询最短路径数据，举例 f,h 不具备连通性，查询两点间最短路径是 f,c,e,b
④将各组最短路径整合为一条完整路径
