宽带前馈ANC
宽带前馈ANC的组成部分有:
单个参考传感器(麦克风),单个次级声源,单个误差传感器。
这种类型的ANC系统被简化之后的单通道管式ANC系统框图如下图1所示:
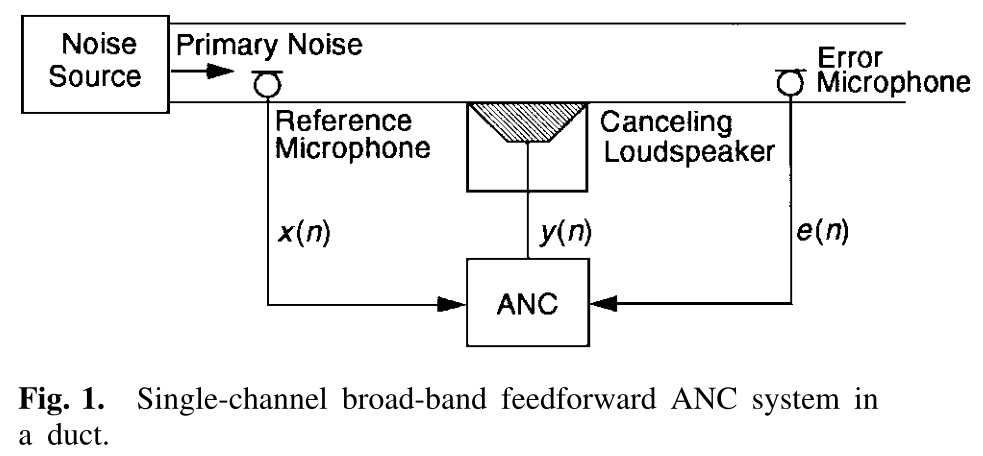
其中输入信号,也就是参考信号被参考麦克风采集;
参考信号被采集之后,通过ANC系统的处理,去驱动一个麦克风(次级麦克风);
而误差麦克风用来对ANC系统进行监测。
整个ANC系统中,控制系统的最终目标是最小化(误差扬声器中)所监测到的声学噪声。
宽带前馈ANC的基础理论
宽带前馈ANC系统如上所示,是一种自适应的识别框架,由上面的图1,进一步细化得到下面的图2
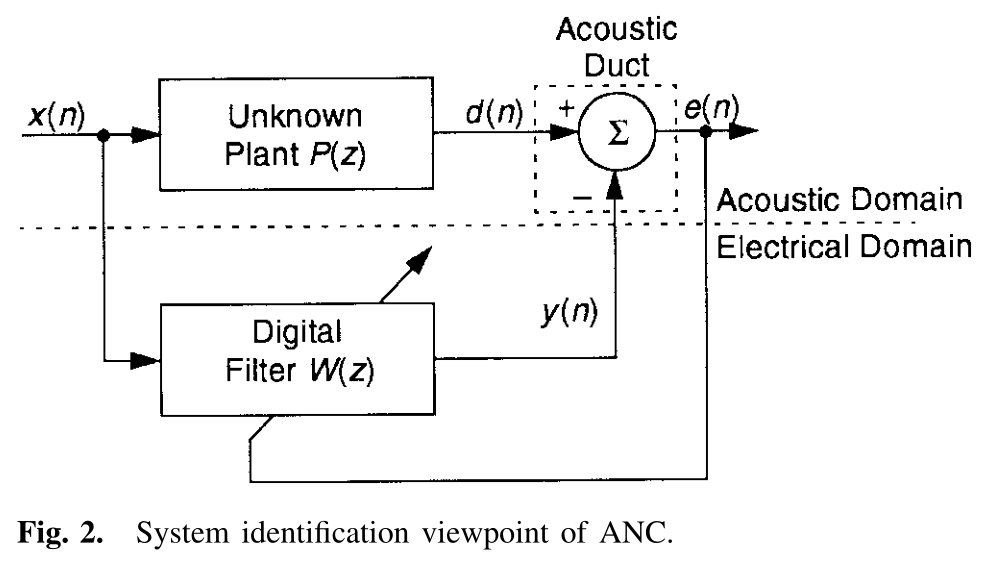
其中\(P(z)\)表示初级通道,为从参考传感器到误差传感器之间的声学通路的冲激响应,在此路径下噪声从被参考传感器采集直到传播到误差传感器,这之间会存在一定的衰减,\(P(z)\)就是表示这一过程的传递函数,但是\(P(z)\)的具体形式还是未知的。
\(W(z)\)为一个参数可更新的自适应滤波器,被用来对上面的未知对象\(P(z)\)进行估计。
如果上面的对象是动态的,也就是\(P(z)\)并非是固定的,那么上面的自适应算法有能力连续追踪系统的动态变化。
与传统表示识别方案的系统框图不同的是,上面图2中的Acoustic Duct部分使用了减法而非传统框图中使用声学求和节点。为保持一致性,我们将会继续使用减法来表示声学求和的节点,因为这仅仅改变一下正负号即可。
上面的自适应滤波器\(W(z)\)的优化目标是最小化残余的误差信号\(e(n)\)。
根据上面的图2,当自适应滤波器\(W(z)\)收敛之后,\(E(z)=0\),如果\(X(z)\ne0\)我们紧跟着就会有\(W(z)=P(z)\),这意味着此时\(y(n)=d(n)\)。也就是说此时自适应滤波器的输出\(y(n)\)与参考噪声通过未知系统\(P(z)\)之后的初级干扰\(d(n)\)完全相同。
此时当\(d(n)\)和\(y(n)\)在声学意义上相叠加之后,此时的残余误差\(e(n)=d(n)-y(n)=0\),也就是说根据叠加原理,最终这两个声音信号得到了完美的抵消。
ANC系统的表现好坏由残余误差信号\(e(n)\)的频域分析所决定,\(e(n)\)的自功率谱由下式给出:
其中\(C_{dx}(w)\)是两个广义平稳随机过程\(d(n)\)和\(x(n)\)的振幅平方相干函数,\(S_{dd}(w)\)是\(d(n)\)的自功率谱。
上面的等式指出,ANC系统的表现取决于相干性,相干性是对噪声和\(x(n),d(n)\)两个过程的相对线性度的度量。
为了使得残余噪声\(e(n)\)尽可能小,必须使得在存在显著干扰能量的频率位置上有着较强的相干性\(【C_{dx}(w)\approx1】\)
ANC系统在频率\(w\)时的最大降噪量(分贝)为\(-10log_{10}[1-C_{dx}(w)]\)。
如上面图1所示,参考信号被参考麦克风拾取之后,控制器会花一定的时间计算出正确的输出传递给抵消扬声器。如果这种电路的延时超过从参考扬声器到抵消麦克风的声学延时,那么系统的表现将会严重的退化。这是因为当电路延时超过声学延时,此时的控制器的响应是非因果的。
当因果性得到满足,ANC系统能够消除宽带的随机噪声,注意当因果性不能满足时,系统只能有效的控制窄带噪声或者周期噪声。
次级路径的影响
ANC系统中自适应滤波器的应用如图1所示,它的使用是很复杂的,因为在图2中的声学求和处的节点表示了从抵消扬声器到误差麦克风的之间的空间中的声学叠加,但是我们所需要实现的是参考麦克风处的初级噪声与自适应滤波器的输出相叠加从而达到抵消噪声的目的,因此有必要对次级路径传递函数\(S(z)\)也就是从\(y(n)\)到\(e(n)\)的传递函数进行补偿,其中还包括了数模(D/A)转换器、重建滤波器、功率放大器、扬声器、从抵消扬声器到误差麦克风的声路、误差麦克风、前置放大器、抗混叠滤波器和模拟到数字(A/D)转换器。
为了便于分析,我们采用图3中的实际系统来替换图2中的框图。
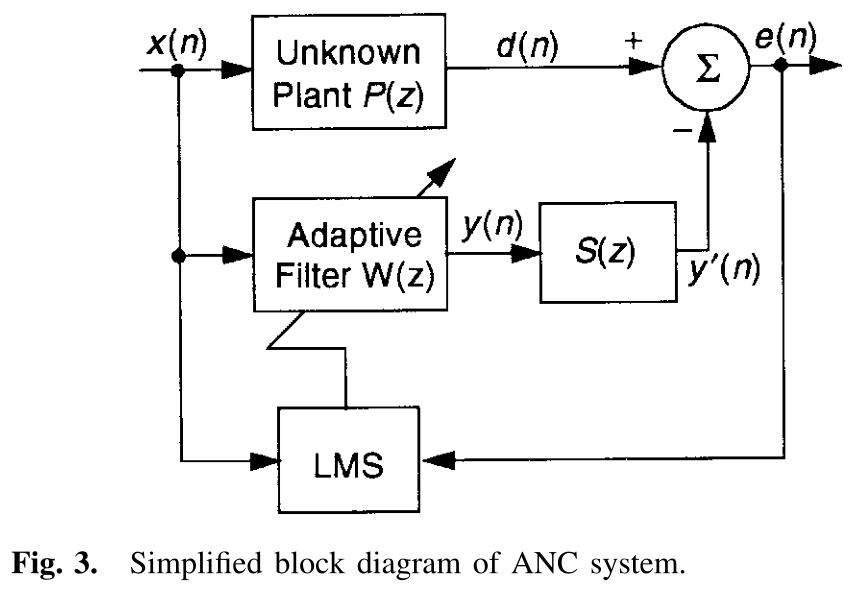
图3中,误差信号\(e(n)\)的z变换为:
上面之前(1)式中所讨论提到,残余误差受到参考信号的相干性的限制。
为了简化分析,我们将问题简化,假设自适应滤波器收敛,残余误差达到理想值为0,\(E(z)=0\),那么就需要实现最佳的传递函数
换句话说,自适应滤波器\(W(z)\)必须要同时建模\(P(z)\)和反向建模\(S(z)\)。
这种方法的一个关键性的优点是,在有着合适的对象模型之后,系统可以根据噪声声源的变化所引起的输入信号(此处应该指的是输入的参考信号\(x(n)\))变化而即时做出响应。
然而,ANC系统的性能在很大的程度上取决于次级路径上的传递函数。
通过引入均衡器,可以获得更加均匀的次级路径频率响应,降噪量可以显著增加。
除此之外,需要一个足够高阶的自适应FIR滤波器,来逼近式(3)中的有理函数\(\frac{1}{S(z)}\)。
如果初级路径\(P(z)\)中不包含至少相等长度的延时,则无法补偿由于\(S(z)\)导致的固有延时。
Filtered - X - LMS 算法
图3中所示的使用标准的LMS算法将次级路径引入控制器中,通常会导致不稳定。这是因为因为由于次级路径\(S(z)\)的存在导致误差信号不能与参考信号正确的“时间对齐”。
有大量的方案可以补偿\(S(z)\),Morgan提出两种解决这个问题的方法。
第一个解决方法是,放一个逆滤波器\(\frac{1}{S(z)}\)与\(S(z)\)进行串联,来消除\(S(z)\)所带来的影响。
第二个解决方法是,在LMS算法的权重更新过程中,在参考信号的路径中放置一个与\(S(z)\)相同的滤波器,实现所谓的Filtered-X-LMS(FXLMS)算法。
由于\(S(z)\)的逆系统不一定存在,所以FXLMS算法通常是最有效的方法。
(1) FXLMS算法的推导
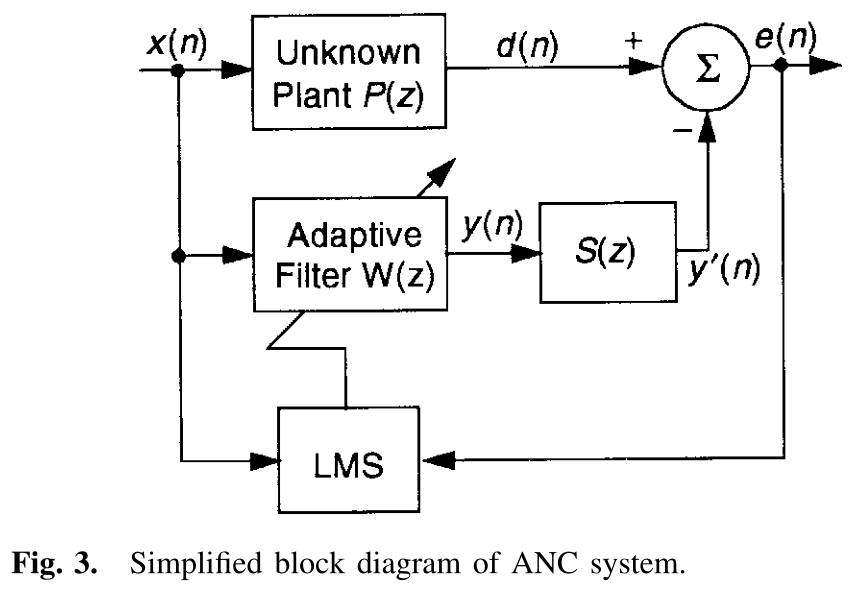
上面图3显示了位于LMS算法控制更新的数字滤波器\(W(z)\)的后面的次级路径的传递函数\(S(z)\)在系统中的位置。
则根据上图系统关系,残余误差信号\(e(n)\)可以表示为:
其中\(n\)表示信号的时间序列索引;\(s(n)\)表示次级路径的冲激响应;\(*\)表示线性卷积;
\(w(n)=[w_{0}(n),w_{1}(n),......,w_{L-1}(n)]^T\)表示\(W(z)\)的系数;
\(x(n)=[x(n),x(n-1),......,x(n-L+1)]^T\)表示信号向量;
\(L\)是滤波器阶数,\(W(z)\)必须要足够高阶以能够准确的建模出物理系统的响应。
假设均方代价函数为\(\xi(n)=E[e^{2}(n)]\),那么自适应滤波器将最小化瞬时均方误差:
使用最陡下降方法,用步长\(\mu\)来从负梯度方向上更新系数向量\(w(n)\),更新计算公式为:
其中\(\bigtriangledown\hat{\xi}(n)\)是\(n\)时刻的均方误差(MSE)的瞬时估计,
根据上面的(4)式:\(e(n)=d(n)-s(n)*[w^{T}(n)x(n)]\tag{4}\),\(e(n)\)对\(w(n)\)求导,得到\(\bigtriangledown e(n)=-s(n)*x(n)=-x'(n)\),此处将\(x'(n)\)定义为:\(x'(n)=s(n)*x(n)\)。
将\(\bigtriangledown e(n)=-x'(n)\) 代入\(\bigtriangledown\hat{\xi}(n)=\bigtriangledown e^{2}(n)=2[\bigtriangledown e(n)]e(n)\)中,得到\(\bigtriangledown\hat{\xi}(n)\)的新的表达式:
代入(6)式,得到FXLMS算法的更新过程:
在实际的ANC系统中,\(S(z)\)是未知的,故\(\bigtriangledown e(n)=-s(n)*x(n)=-x'(n)\)同样未知,故需要对额外的滤波器\(\hat{S}(z)\)进行估计。
因此,通过将参考信号\(x(n)\)通过这个估计的次级路径\(\hat{s}(n)\)来生成\(x'(n)\)作为滤波器的参考信号:
其中\(\hat{s}(n)\)是估计出来的次级路径\(S(z)\)的冲激响应。使用FXLMS算法的框图如下图图4所示:
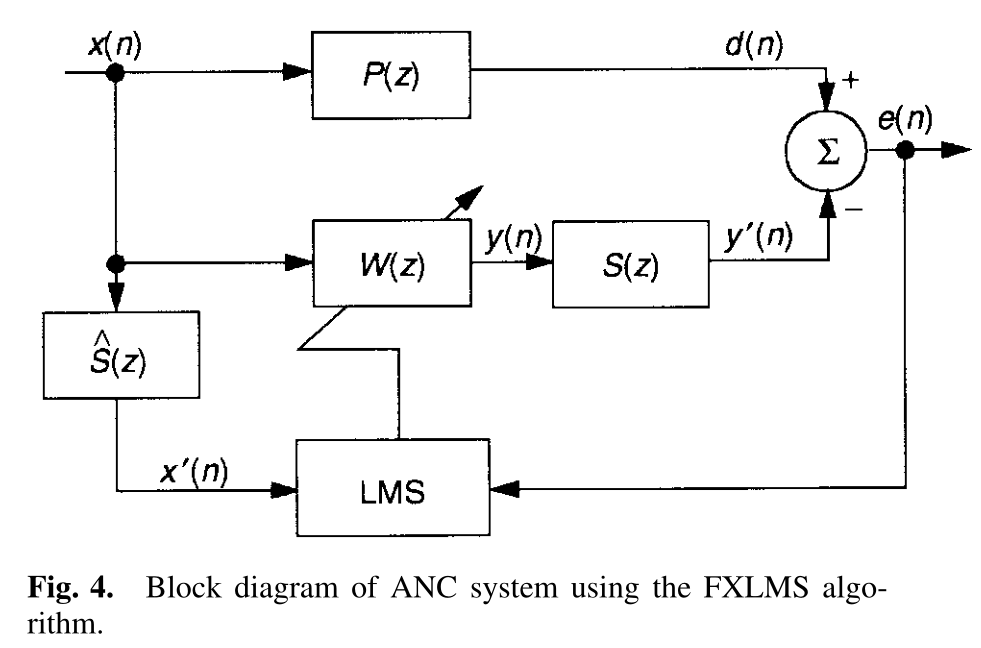
FXLMS算法似乎对滤波器\(\hat{S}(z)\)估计\(S(z)\)过程中产生的错误非常的宽容。
如Morgan所言,在慢适应的限制下,算法最终将使得\(S(z)\)和\(\hat{S}(z)\)之间以接近90°的相位的误差进行收敛。
因此,对于大多数ANC应用,离线建模的方法被用来在最开始的训练阶段来估计\(S(z)\)。
(2)FXLMS算法的分析
考虑到控制滤波器\(W(z)\)变化非常缓慢的情况,所以上面图4中的\(W(z)\)和\(S(z)\)的顺序可以进行互换,如果再令\(\hat{S}(n)=S(n)\),简化之后得到图5:
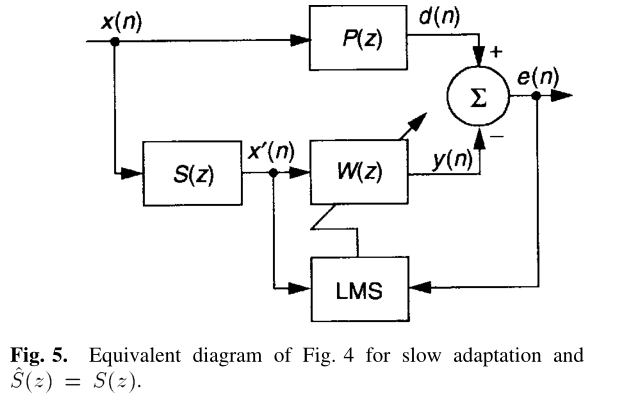
由于自适应滤波器\(W(z)\)的输出\(y(n)\)现在是直接传递给误差信号\(e(n)\),因此可以使用传统的LMS算法分析的方法,尽管现在的参考信号(期望信号)\(x'(n)\)是\(x(n)\)通过\(S(z)\)得到的。
如果自适应算法的速度慢,即步长\(\mu\)设置较小,那么这种方法可以给出比较准确的结果。
用在FXLMS算法中的最大迭代步长为:
其中,\(P_{x'}=E[x'^{2}(n)]\)是滤波器参考信号\(x'(n)\)的功率,$\bigtriangleup $是与次级路径中的总的延迟相对应的样本数量。因此,次级路径中的延迟通过减小FXLMS算法中的最大步长来影响ANC系统的动态响应。
在宽带情况下出现的另一个复杂的情况是,测量噪声\(u(n)\)和\(v(n)\)分别存在于参考信号\(x(n)\)和误差信号\(e(n)\)中。
最优的无约束的传递函数为:
上面关于\(w^{o}(z)\)的等式关系说明,最优无约束滤波器\(w^{o}(z)\)与误差传感器中的测量噪声\(v(n)\)无关。
然而,参考传感器中的测量噪声\(u(n)\)确实对最优滤波器的最佳权系数有影响,并且会降低降噪性能。
控制器的最佳频率响应,是通过控制器消除初级噪声和放大测量噪声之间的折衷,具体如何选择,参看相关文献。
延时FXLMS算法
在图4中,如果次级路径的传递函数被建模为仅仅只有延时,那么则可以用延迟替代,FXLMS算法的这种特殊的情况也被称为延时FXLMS算法。此时算法迭代过程中下降步长的上限值取决于延时量,并且与式(10)中的Elliott近似值非常一致。因此,应该尽量保持较小的延时,例如选择减小误差传感器和次级麦克风之间的距离,并且尽量减小电路元件的延时。
(3)泄露FXLMS算法
在ANC系统中,直接使用FXLMS算法有时会带来另一个问题:与低频共振相关的较高的噪声声级,这可能会导致次级扬声器的过载,从而产生非线性失真。
解决这个问题的一个方法是对滤波器输出功率进行限制,通过将之前的代价函数修改为新的形式:
来实现这一效果。
其中\(\gamma\)是控制具体限制效果的权重系数,根据FXLMS算法的推导过程,则之前的滤波器系数更新过程可以重新推导为:
其中此处的\(\nu=1-\mu \gamma\)是泄露系数,其取值范围为\(0<\nu<1\)。这种泄露FXLMS算法在一定程度上还减少了有限精度实现过程中的产生的数值错误。
泄露因子的引入对自适应算法的稳定起到了很大的作用,特别是当使用到的声源的强度较大时(此处可能指的是实际电路系统搭建过程中所使用到的次级扬声器的规格较大时)。
(4)反馈所带来的影响和解决的方法
上面图1中所展示的ANC系统是采用了一个参考麦克风来对参考噪声进行拾取,然后将这个作为输入送进自适应滤波器,产生一个反声\(y(n)\)在管道中抵消初级噪声。
然而不幸的是,这个次级扬声器输出的反声\(y(n)\)同时也会向上游辐射,传播到参考麦克风处,导致参考麦克风拾取的参考信号\(x(n)\)出现损坏。
从次级扬声器(抵消扬声器)到参考麦克风这一段路径处的发生的声波耦合现象称为声音反馈。
在振动ANC系统中,由于控制致动器和参考传感器之间的反馈,有时也会发生类似的现象。
下面的图6显示了更一般的ANC系统的框图。
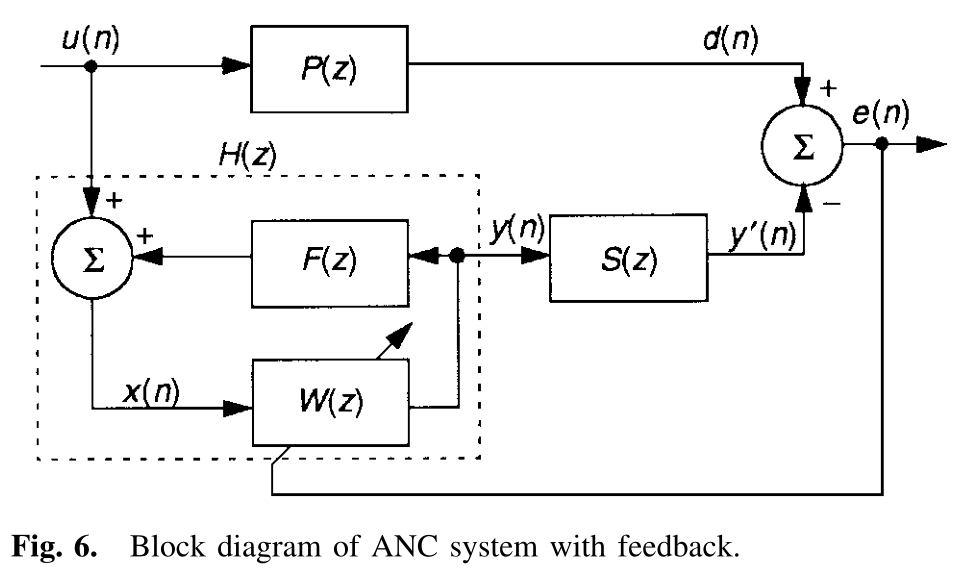
上面图6中包含了从次级声源到参考麦克风的反馈路径传递函数\(F(z)\)。
上面框图中,\(u(n)\)表示初级噪声,\(x(n)\)表示参考扬声器中拾取的信号,注意此时由于声音反馈现象的存在,初级噪声\(u(n)\)不再完全等于自适应滤波器的参考信号\(x(n)\)。
\(F(z)\)表示自适应滤波器的输出\(y(n)\)传播到参考传感器之间的反馈路径的传递函数。
则此时自适应滤波器达到稳态时候的传递函数表示为:
上面(14)式的具体推导过程如下:
给上面的图6上的两个加法节点分别命名为A和B,得下图:
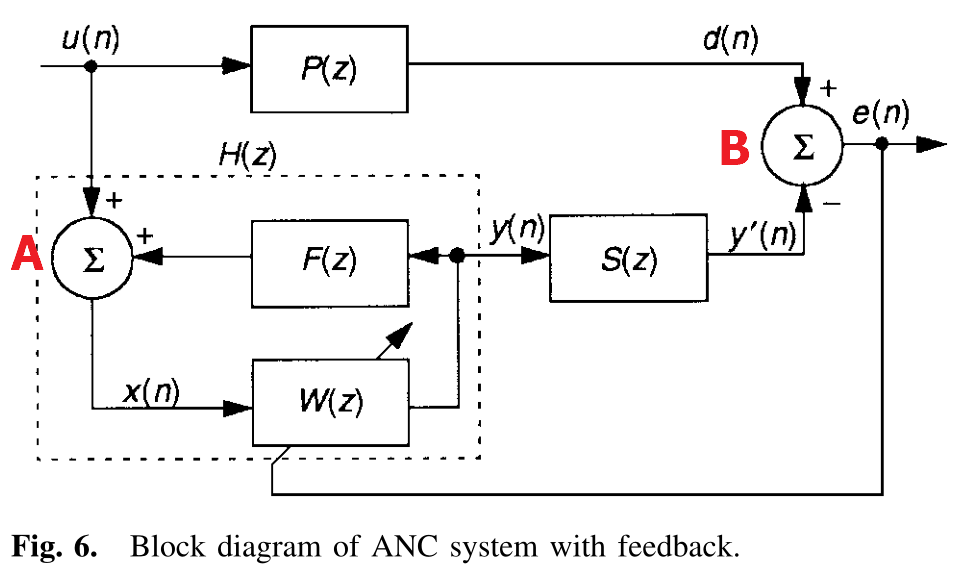
根据A节点可得方程:\(X(z)=U(z)+F(z)X(z)W(z)\)
可以解出\(X(z)\)的表达式:\(X(z)=\frac{U(z)}{1-F(z)W(z)}\)
则可得B节点处的输入\(y'(n)\)的Z域表达式:\(Y'(z)=X(z)W(z)S(z)=\frac{U(z)W(z)S(z)}{1-F(z)W(z)}\)
当误差信号\(e(n)=0\)时,则有\(Y'(z)=D(z)\),即:
化简即可得出:
FXLMS算法的仿真:
% matlab官方案例中次级路径的建模生成
%% 生成次级通道的传递函数
clc;clear; close all;
Fs = 4e3; % 采样率 8 kHz
N = 60; % 800 个采样点数,总共时间 0.1 seconds
Flow = 160; % 低频边界: 160 Hz
Fhigh = 2000; % 最高频率边界: 2000 Hz
delayS = 7;
Ast = 20; % 20 dB 阻带衰减
Nfilt = 8; % 滤波器的阶数
% Design bandpass filter to generate bandlimited impulse response
filtSpecs = fdesign.bandpass('N,Fst1,Fst2,Ast',Nfilt,Flow,Fhigh,Ast,Fs);
bandpass = design(filtSpecs,'cheby2','FilterStructure','df2tsos', 'SystemObject',true);
% Filter noise to generate impulse response
secondaryPathCoeffsActual = bandpass([zeros(delayS,1); log(0.99*rand(N-delayS,1)+0.01).* sign(randn(N-delayS,1)).*exp(-0.01*(1:N-delayS)')]);
secondaryPathCoeffsActual = [zeros(delayS,1); log(0.99*rand(N-delayS,1)+0.01).* sign(randn(N-delayS,1)).*exp(-0.01*(1:N-delayS)')];
secondaryPathCoeffsActual = secondaryPathCoeffsActual/norm(secondaryPathCoeffsActual);
figure(1)
t = (1:N)/Fs;
plot(t,secondaryPathCoeffsActual,'b');
xlabel('Time [sec]');
ylabel('Coefficient value');
title('True Secondary Path Impulse Response');
%% 对上面产生的次级通道进行估计
order = 75; % 我们所估计的次级通道的传递函数的阶数
Sw=secondaryPathCoeffsActual/5; % 真实的次级通道传递函数系数
lengthSimSignal = 50000; % 用来进行测试次级通道的白噪声输入信号的采样点数
x_iden=randn(1, lengthSimSignal); %generating white noise signal to estimate S(z)
% x_iden 为估计S(z)所需要用到的输入信号
% send it to the actuator, and measure it at the sensor position,
y_iden=filter(Sw, 1, x_iden); % x_iden送入系统S(z),产生经过真实的次级路径之后的输出信号y__iden
% Then, start the identification process
% 开始进行次级通道识别估计
statex=zeros(1,order); % 估计过程中输入信号的此刻的状态缓存
Sw_estimate=zeros(1,order); % 估计出来的次级通道传递函数的系数
err_iden=zeros(1, lengthSimSignal); % 每次估计迭代中的识别误差
%LMS 算法估计次级通道Sw
% 相当于用白噪声信号作为输入,白噪声经过系统S(z)之后的输出信号作为LMS算法的期望信号,从而估计S(z)系统
mu=0.001;
for k=order : (length(x_iden))
statex = x_iden(k: -1: (k - order +1)); % 此时系统的输入信号,u(n), u(n-1), u(n-1),.....,u(n-16+1)
y_iden_estimate=sum(statex.*Sw_estimate); % 经过我们估计出的有误差的次级通道之后的模拟输出信号
err_iden(k)=y_iden(k)-y_iden_estimate; % y_iden(k)为通过真实的次级通道之后的期望信号
Sw_estimate=Sw_estimate+mu*err_iden(k)*statex;
end
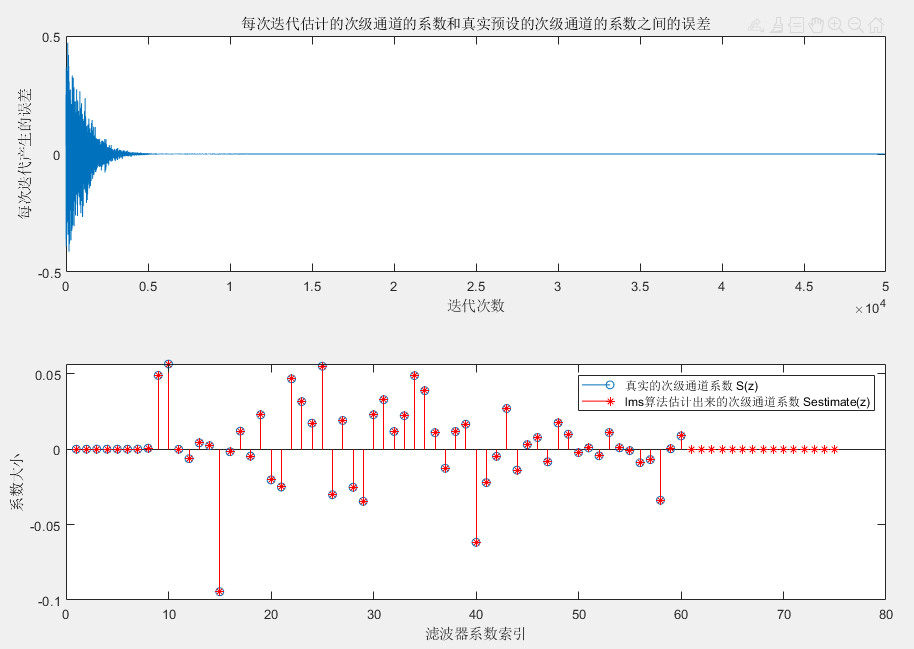
figure
subplot(2,1,1)
plot([1: length(x_iden)-order+1], err_iden(order: length(x_iden)))
ylabel('每次迭代产生的误差');
xlabel('迭代次数');
title('每次迭代估计的次级通道的系数和真实预设的次级通道的系数之间的误差');
subplot(2,1,2)
stem(Sw)
hold on
stem(Sw_estimate, 'r*')
ylabel('系数大小');
xlabel('滤波器系数索引');
legend('真实的次级通道系数 S(z)', 'lms算法估计出来的次级通道系数 Sestimate(z)')
%% 次级通道估计完成之后,使用FXLMS算法估计控制器Wz的滤波器系数,使得参考麦克风采集到的初级噪声xn通过Wz系统之后
% 能够产生一个与xn通过初级通道Pz之后的信号dn完全相同的抵消声波信号yn
lengthx = 10000;
xn=randn(1,lengthx);
% 经过初级路径之后到达误差麦克风的信号d(n)
Pw = 1 * Sw;
dn=filter(Pw, 1, xn);
orderW = 80; % 控制器的阶数
orderS_esti = length(Sw_estimate);
orderS_real = length(Sw);
Cw=zeros(1,orderW); % C(z) 控制器的自适应滤波器的权重系数
Sy = zeros(1, lengthx);
en=zeros(1,lengthx); % 误差传感器进行噪声消除之后的误差
Cy= zeros(1, lengthx); % 控制器的输出
x_n = zeros(1, lengthx);
mu=0.1; % learning rate
for k=orderW: lengthx
Cx = xn(k : -1: k - orderW + 1); % 控制器接收到的输入信号
Cy(k)=sum(Cx.*Cw); % 控制器的输出
Sx=Cy(k : -1: k - orderS_real +1); % 控制器的输出信号也要经过次级路径才能到达误差传感器,这是即将进入次级路径的控制器的输出信号
Sy(k) = sum(Sx .* Sw');
en(k)=dn(k)-Sy(k); % 控制器的输出信号经过次级路径之后,与参考麦克风接收的参考信号经过初级路径传播之后生成的dn信号相减,计算误差
x_n(k) = sum(xn(k : -1: k - orderS_esti +1) .* Sw_estimate);
dn_state=x_n(k : -1: k - orderW +1 );
Cw=Cw + mu*en(k)*dn_state;
end
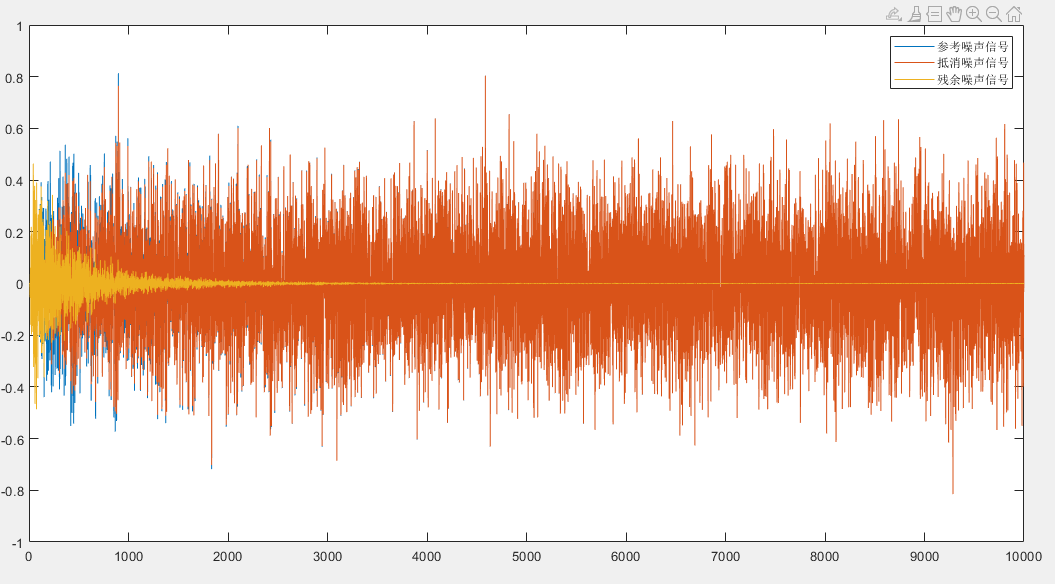
figure
plot([1: lengthx], dn, [1: lengthx], Sy, [1: lengthx], dn-Sy);
legend("参考噪声信号","抵消噪声信号","残余噪声信号")
仿真结果:
参考资料:
Active Noise Control: A Tutorial Review,SEN M. KUO AND DENNIS R. MORGAN
有源噪声控制,陈克安
https://github.com/qiujianben/Active-Noise-Control---DSP2017/blob/master/ActiveNoiseControl.docx


 浙公网安备 33010602011771号
浙公网安备 33010602011771号