维纳（wiener）滤波器以及维纳滤波器的语音增强
线性最优滤波问题
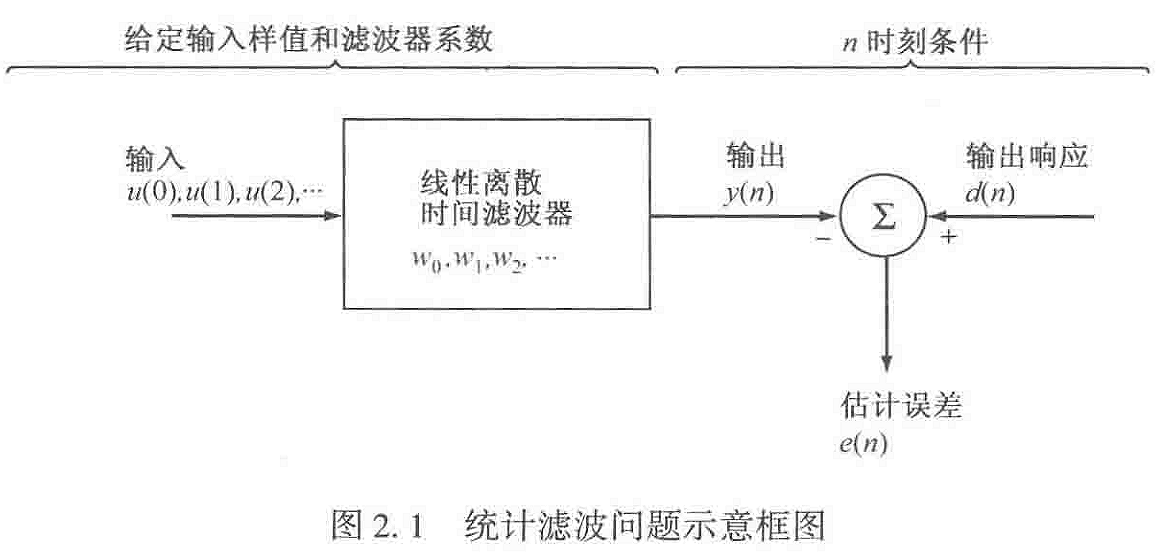
滤波器的输入时间序列为\(u(0), u(1), ...\)
滤波器用其冲激响应\(w(o),w(1),...\)进行表示，
在离散时刻\(n\)滤波器输出为\(y(n)\)
期望响应为\(d(n)\)，期望响应与滤波器输出之间的估计误差用\(e(n)\)表示。
统计优化准则的选择
在滤波器优化设计中，可以考虑采用某种最小代价函数或者某个性能指标来衡量滤波器的优化，一般有：
- 估计误差的均方值；
- 估计误差绝对值的期望值；
- 估计误差绝对值的三阶或高阶期望值。
在这里我们选择均方误差准则。
则线性滤波器的问题可以阐述为：
给定一个输入抽样序列\(u(0), u(1), u(2),...\)设计一个线性离散滤波器，这个线性离散滤波器的输出\(y(n)\)提供了期望响应\(d(n)\)的一个估值，现在需要求解滤波器的系数，使得其估计误差的均方值\(e(n)\)(期望响应\(d(n)\)与实际响应\(y(n)\)之差)为最小。
正交性原理
对于上面提到的随机信号滤波的问题。滤波器的输入用时间序列\(u(0), u(1), ...\)表示，冲激响应用\(w(o),w(1),...\)表示，设它们都是复值且无限长度的。n时刻的滤波器输出为输入和滤波器的线性卷积：
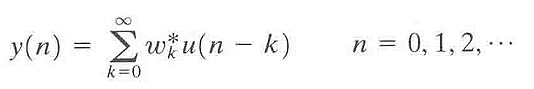
滤波器的目的是要产生一个期望响应\(d(n)\)的估值，设滤波器输人序列\(u(n)\)和期望响应\(d(n)\)是联合广义平稳随机过程(互相关函数只与时间差有关)，且均值为零。如果输人序列\(u(n)\)和期望响应\(d(n)\)均值不为零，则在滤波之前先从输人序列\(u(n)\)和期望响应\(d(n)\)中减去均值，估计值\(d(n)\)自然带有误差，该误差定义为:
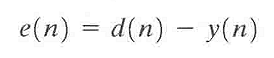
估计误差\(e(n)\)是一个随机变量的抽样值。为了优化滤波器的设计，选择\(e(n)\)的最小均方值为优化目标。因此，定义代价函数为均方误差:
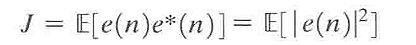
定义一个计算梯度的算子用于计算代价函数\(J\)的多维复值梯度向量\(\bigtriangledown J\)，其中复值梯度向量中的第\(k\)个元素为：
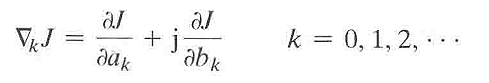
我们现在是要优化这个滤波器，也就是从代价函数\(J\)中得到\(J\)的最小值，此时多维复值梯度向量\(\bigtriangledown J\)中的所有元素都必须同时等于0，即\(\bigtriangledown _{k}J=0,k=0, 1,2,...\)，当此约束条件满足时，即为此滤波器在均方误差意义下达到最优。
而多维复值梯度向量\(\bigtriangledown J\)为：
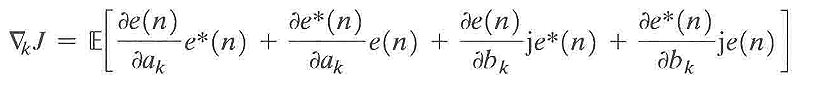
其中：
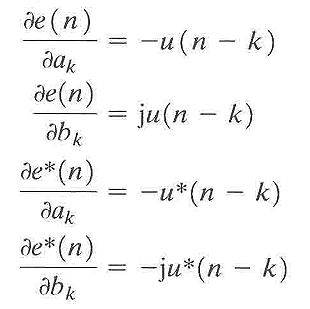
代入，整理得到：
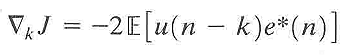
要想使\(\bigtriangledown _{k}J=0,k=0, 1,2,...\)，等价于使得：
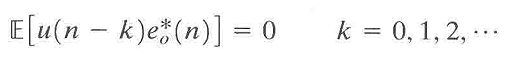
这就是正交性原理，具体可表述为：
使代价函数\(J\)获得最小值的充要条件是其对应的估计误差\(e_{0}(n)\)正交于\(n\)时刻进入期望响应估计的每个输入样值\(u(n)\)。它是线性优化滤波理论中的最重要原理之一，是为验证线性滤波器是否工作于最优状态的数学基础。
维纳-霍夫方程
上面的正交性原理是线性最优滤波器的充要条件，将\(e^{*}_{0}(n)\)的表达式代入，得到：
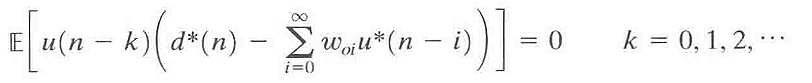
其中\(w_{oi}\)表示优化滤波器（\(w_{o}\)）的第\(i\)个滤波器系数，整理上式得：
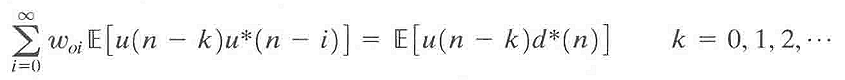
其中，期望\(E[u(n-k)u^{*}(n-i)]\)等于相隔\(i-k\)个延迟的滤波器输入信号\(u(n)\)的自相关系数，换成\(r(i-k)\)表示，即：
\(r(i-k)=E[u(n-k)u^{*}(n-i)]\)
右边等式中的期望\(E[u(n-k)d^{*}(n)]\)等于滤波器的输入\(u(n-k)\)与期望响应\(d(n)\)相隔\(-k\)个时刻的互相关，用\(\rho(-k)\)表示，即：
\(\rho(-k)=E[u(n-k)d^{*}(n)]\)
则上面的关于最优滤波器的系数\(w_{oi}\)的方程可以改写成：
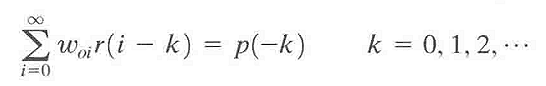
上面方程用两个相关函数定义了最优滤波器的系数，其中一个相关函数是滤波器输入\(u(n)\)的自相关函数，另一个相关函数是滤波器输入\(u(n)\)与期望响应\(d(n)\)的互相关函数。这个方程即为维纳一霍夫(Wiener-Hopf)方程。
维纳一霍夫(Wiener-Hopf)方程的矩阵形式
上面的关于最优滤波器的系数\(w_{oi}\)的方程可以改写成矩阵形式
其中，系数矩阵\(R\)为:
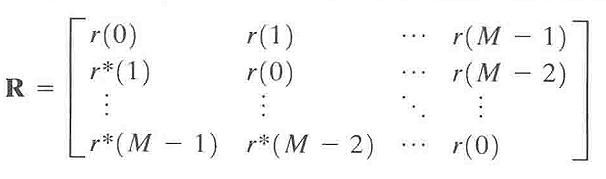
右边的常数项列向量\(p\)为：
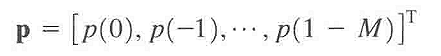
\(w_{0}\)为均方误差意义上最优滤波器的\(M\)个抽头组成的滤波器系数向量：
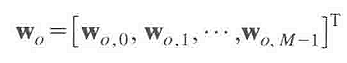
若相关矩阵\(R\)可逆，则可利用上面的矩阵方程求解出最优滤波器的系数向量\(w_{o}=R^{-1}p\) ，求解过程需要知道两个条件：
- 输入信号\(u(n)\)的相关矩阵；
- 输入信号\(u(n)\)和期望响应\(d(n)\)的互相关向量\(p\)
matlab仿真
以含白噪声的正弦信号为例，matlab仿真如下：
clc;clear; close all;
N = 4000;
fs = 2000;
n = (1 : N) / fs;
dn = 2 * sin(2 * pi * 1 * n) ;
un = dn + randn(size(dn));
plot(n, dn, n, un);
M = 100; % 滤波器阶数
Rxx = xcorr(un);
for i = 1 : N -1
Rx(i) = Rxx(N - 1 + i);
end
pxx = xcorr(un, dn);
for i = 1: N-1
px(i) = pxx(length(pxx) - (N-1) - i);
end
R = zeros(M, M); % 输入信号u(n)的相关矩阵
for i = 1: M
for j = 1 : M
R(i, j) = Rx(abs(i-j) + 1);
end
end
p = zeros(M, 1); % 输入信号u(n)与期望响应d(n)的互相关向量
for i = 1: M
p(i) = px(i);
end
yn = zeros(1, length(un));
w = inv(R) * p; % 滤波器系数w(n)
for i = length(w) + 1 : length(un)
y = 0; % 用来保存当前滤波器系数与输入信号的加权相乘滤波之后的结果
for k = 1 : length(w)
y = y + w(k) * un(i - length(w) + k); % 用之前输入的若干个信号和滤波器系数线性相乘，得到滤波之后结果
end
yn(i - length(w)) = y;
end
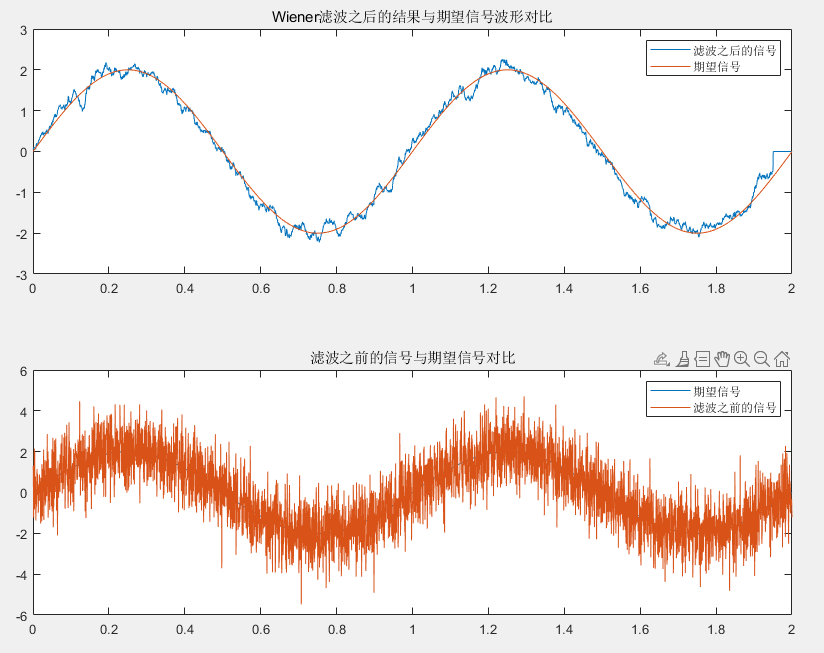
subplot 211
plot(n, yn, n, dn)
title("Wiener滤波之后的结果与期望信号波形对比")
legend("滤波之后的信号", "期望信号")
subplot 212
plot(n, dn, n, un)
title("滤波之前的信号与期望信号对比")
legend("期望信号", "滤波之前的信号")
运行结果：
频域维纳滤波
维纳滤波器应用于语音增强
维纳滤波语音增强的matlab仿真
clc; clear; close all;
[x, fs] = audioread('bluesky.wav');
nx = length(x);
wlen = 0.05 * fs;
inc = 0.05 * fs * 1/2;
figure(1);
t1 = (1: nx)/fs;
subplot 211
plot(t1, x);
title("原始纯净语音信号")
%%
noise = 0.2 * randn(size(x));
%% 滤波200-8000 Hz
[b1,a1]=butter(8,[2000/(fs/2),2500/(fs/2) ]);%获得8阶巴特沃斯滤波器系数，得到2000-2500 Hz的宽带滤波器
noise = filter(b1,a1,noise);%滤波
subplot 212
xNoise = x + noise;
plot(t1, xNoise);
title('加噪语音信号')
% sound(xNoise, fs)
%% 画加噪语音语谱图
xNoiseFrame = enframe(xNoise, fs);
xNoiseStft = stfthw(xNoiseFrame);
speechspec(xNoiseStft, fs, inc);
%% 画原始语音语谱图
xFrame = enframe(x, fs);
xStft = stfthw(xFrame);
speechspec(xStft, fs, inc);
%% wiener滤波器
clean = x;
noisy = xNoise;
noise = xNoise - x;
stftClean = stfthw(enframe(clean, fs));
stftNoise = stfthw(enframe(noise, fs));
stftNoisy = stfthw(enframe(noisy, fs));
[m, n] = size(stftClean);
pxx = zeros(m, 1);
for j = 1: n
pxx = pxx + abs(stftClean(:, j)) .^ 2;
end
pxx = pxx / n;
[m, n] = size(stftNoise);
pnn = zeros(m, 1);
for j = 1 : n
pnn =pnn + abs(stftNoise(:, j) ).^ 2;
end
pnn = pnn / n;
H = (pxx ./ (pxx + pnn)) ;
[m, n] = size(stftNoisy);
y = zeros(size(stftNoisy));
for i = 1 : n
y(:, i) = H .* stftNoisy(:, i);
end
speechspec(y, fs, inc);
%% 将维纳滤波增强后的信号重新合成语音信号
sig = stft2signal(y, fs, '增强之后的语音信号');
sound(xNoise, fs);
pause(5);
sound(sig,fs);
上面所用到的部分函数：
上面所有程序一帧语音长度统一为0.05ms，stft窗函数为hanmming
1，语音分帧
function xframe = enframe(x, fs)
% 给输入信号x进行分帧，帧移位帧长的一半
% 输出信号为分帧之后的矩阵，不同的列表示不同的时间，不同的行表示不同的频率
nx = length(x);
nwin = fs * 0.05;
win = hamming(nwin);
inc = 0.5 * nwin;
nf = fix((nx - (nwin - inc))/inc);
f = zeros(nwin, nf);
indf = inc * (0 : nf - 1);
inds = (1 : nwin )';
index = repmat(indf, nwin, 1) + repmat(inds, 1, nf);
xframe = x(index);
end
2，短时傅里叶变换
function xstft = stfthw(x)
% 对已经完成分帧之后的信号x做stft
[nwin, t] = size(x);
xstft = zeros(size(x));
for i = 1 : t
xstft(:, i) = fft(x(:, i) .* hamming(nwin), nwin);
end
end
3，重叠相加法将时频域的信号合成时域信号
function sig = stft2signal(y, fs, titlename)
% 将时频的信号重新合成语音信号
% 输入y为stft之后的矩阵
% 输入fs为语音信号的时域采样率
% 输入titlename为画图时的图名称
% 输出sig为最终合成的时域语音信号序列
[freqRes, frameNum] = size(y);
wlen = freqRes;
inc = wlen / 2 ;
sig = zeros((frameNum - 1) * inc + wlen, 1);
for i = 1 : frameNum
start = (i - 1) * inc + 1;
spec = y(:, i);
sig(start : start + wlen - 1) = sig(start : start + wlen - 1) + real(ifft(spec, wlen));
end
figure
plot((1:length(sig))/fs, sig)
title(titlename);
end
4，画语谱图的函数
function speechspec(xstft, fs, inc)
% 画出语谱图
[f, t] = size(xstft);
time = ((1 : t) - 1) * inc /fs;
halff = 1 : f/2;
freq = halff / f * fs;
figure
imagesc(time, freq, 10 * log10(abs(xstft(halff, :) .^ 2)));
axis xy;
end
运行结果：
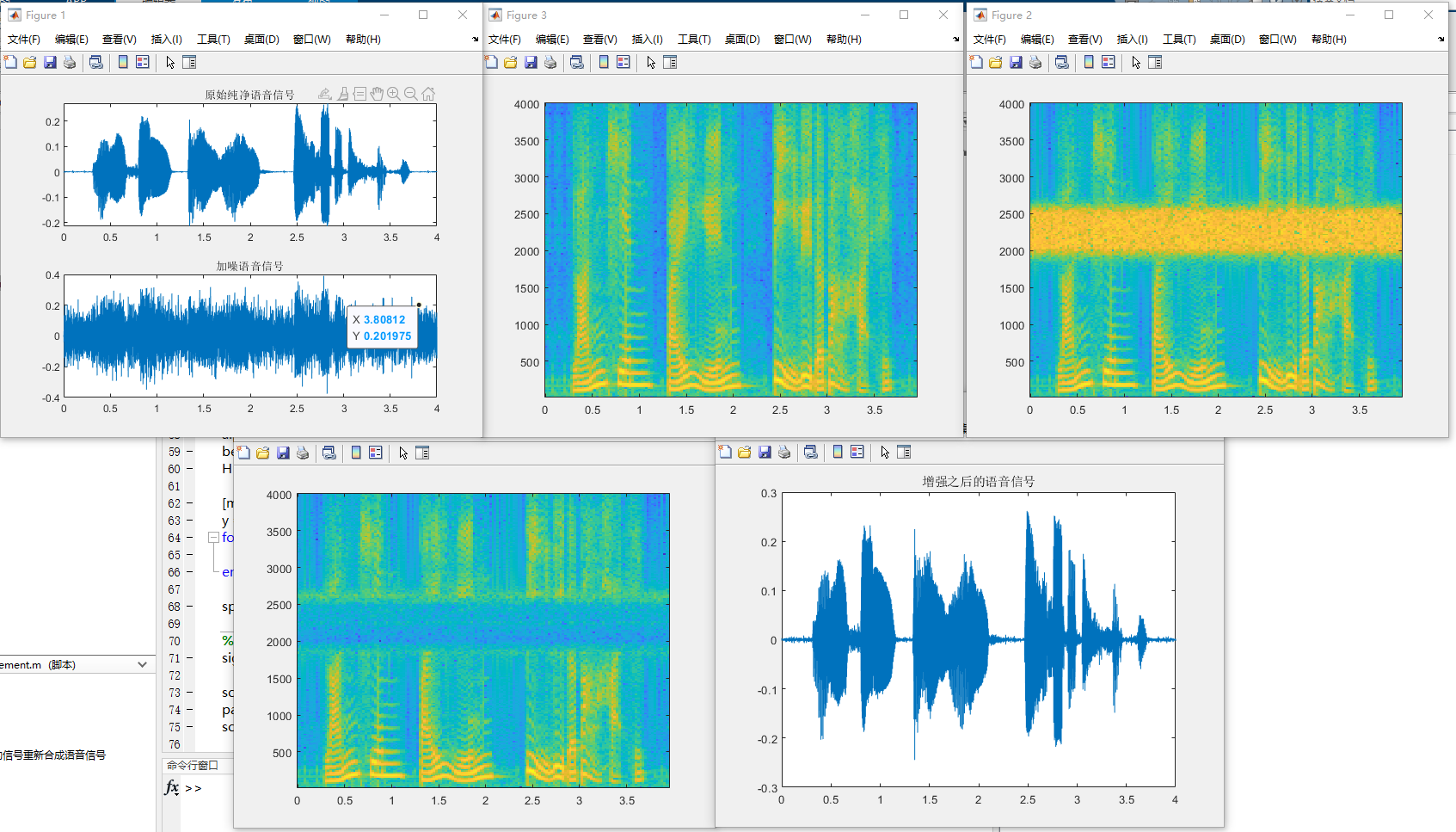
参考文献：
现代信号处理，第3版，张贤达
Matlab语音信号分析与合成，宋知用
自适应滤波器，第5版，Simon Haykin
https://www.bilibili.com/video/BV1sM4y1K7bB/?spm_id_from=333.337.search-card.all.click
