现代功率谱估计(2):Levinson-Durbin递推方法求解AR模型参数
p阶AR模型的差分方程形式和系统函数分别为:
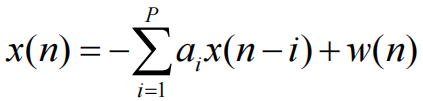
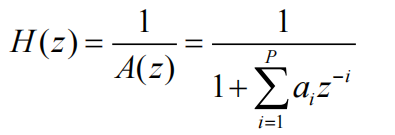
令\(z = e^{jw}\),则AR模型输出的功率谱密度为:
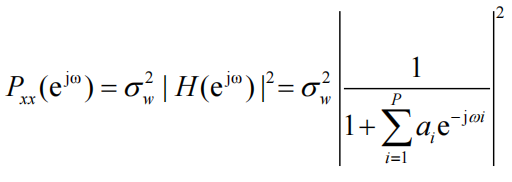
AR模型的系统输出信号为\(x(n)\),计算输出信号的自相关函数:
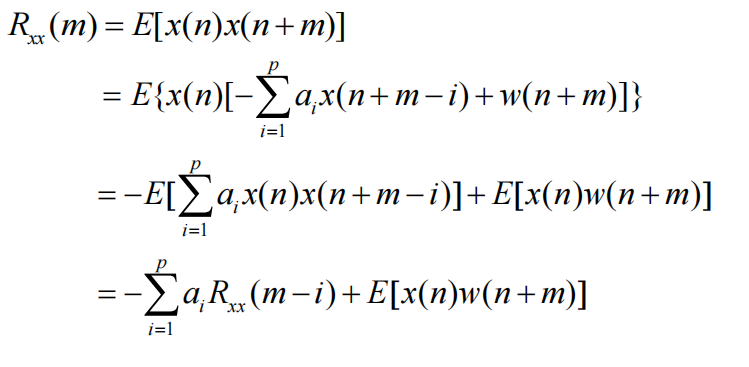
其中最后结果的后面一项,输出信号\(x(n)\)和输入系统的白噪声的互相关函数\(E[x(n)w(n+m)]\)满足关系:
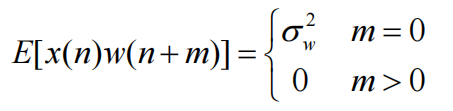
其中\(\sigma^{2}_{w}\)为输入白噪声信号的方差,即噪声功率
因此上面的输入信号\(x(n)\)的自相关函数的最终取值应该分为两种情况讨论,分别式当\(R_{xx}(m)\)中表示时间差的\(m\)取\(m=0\)和\(m\ne0\)时,将\(E[x(n)w(n+m)]\)代入\(R_{xx}(m)\),即:
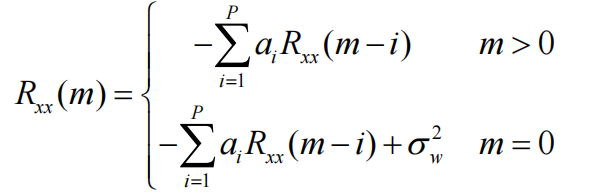
写成矩阵形式的Yuler-Walker方程为:
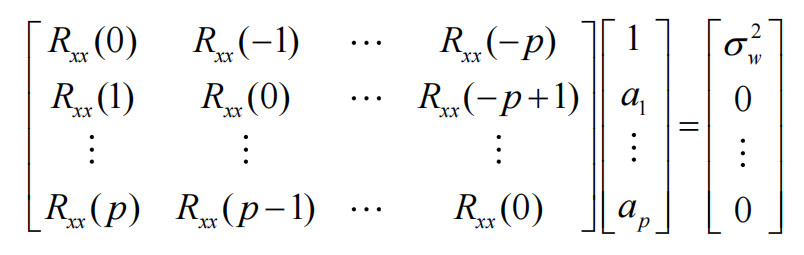
其中实信号的自相关函数满足偶对称,即\(R_{xx}(m)=R_{xx}(-m)\), 则上面的右边的自相关矩阵为Toeplitz矩阵,在确定AR模型阶数为\(p\)时,通过求解AR模型的\(p\)个系数,以及此时AR模型的输入白噪声的功率则可确定输出信号\(x(n)\)的功率谱密度分布。
p阶AR模型的系数分别为\(a_{pi}\),其中\(a\)的下标处第一个表示此时AR模型的阶数,也就是当前阶数情况下总共有几个系数,第二个下标i表示当前系数的序列索引。
以p=1,1阶AR模型为例,则写成矩阵形式的Yuler-Walker方程为:
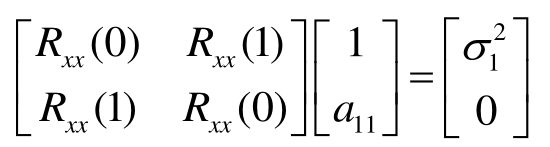
求解未知数\(a_{11}\),\(\sigma^{2}_{1}\)为:
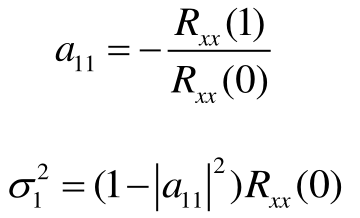
递推到p=2,2阶AR模型情况,写成矩阵形式的Yuler-Walker方程为:
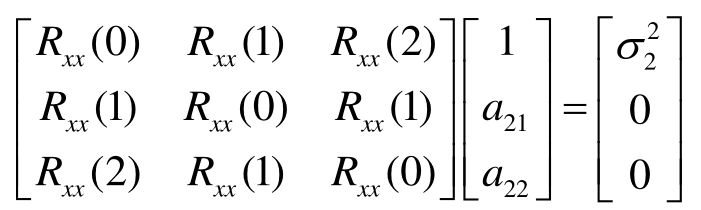
求解p=2,2阶情况下的AR模型系数:
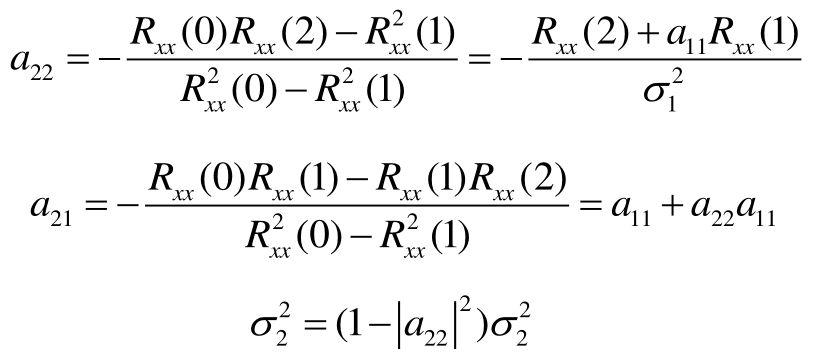
2阶AR模型的系数\(a_{21},a_{22},\sigma^{2}_{2}\)均可通过之前1阶AR模型的系数\(a_{11}\)和估计出的自相关函数得到。
以此类推,k阶AR模型系数\(a_{ki}\),白噪声功率\(\sigma^{2}_{k}\)均可通过第k-1阶AR模型的相关系数得到:
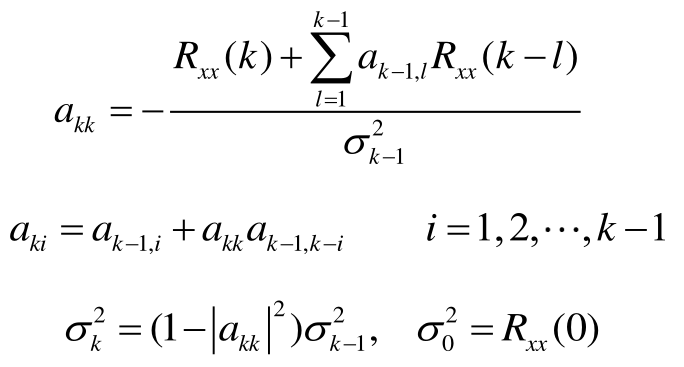
通过不断的往下一阶递推,可以得到较高阶AR模型,流程如下:
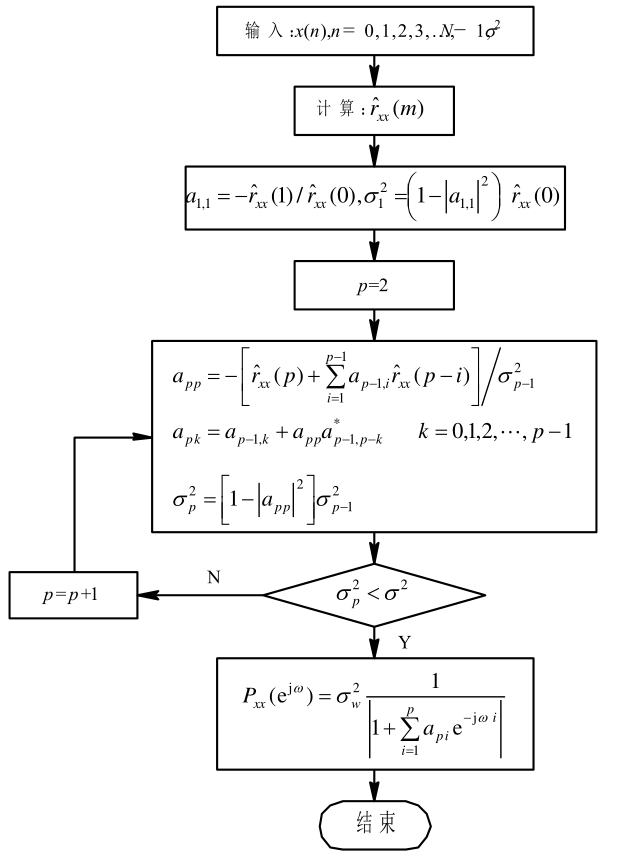
在循环递推开始之前,需要提前估计自相关函数,以及1阶情况的AR模型的相关系数和白噪声功率。
代码如下:
% levinson-durbin递推求解Yuler_Walker方程
clc; clear; close all;
N = 256;
p = 100;
n = 1: N;
fs = 2000;
t = n * 1/ fs;
f1 = 100; f2 = 230;
xn = 2 * sin(2 * pi * f1 * t + pi / 3) + sin(2 * pi * f2 * t + pi / 4) + randn(size(n));
Rx = xcorr(xn, 'biased');
Rxx = zeros(1, p+1);
for i = 1 : p+1
Rxx(i) = Rx(N -1 + i); % Rxx存储值为Rxx(0), Rxx(1), ......, Rxx(p) 共p+1个根据样本估计的自相关值
end
a = zeros(p, p);
sigma2 = zeros(1, p);
% 1阶AR模型的初始值
a(1, 1) = - Rxx(2)/Rxx(1);
sigma2(1) = (1 - a(1, 1)^2) * Rxx(1);
% 从p=2阶开始迭代,一直迭代到p阶
for m = 2 : p % m表示当前迭代的AR模型的总的阶数
a(m, m) = -Rxx(m + 1) / sigma2(m - 1); % m阶AR模型总共m个系数中的第m个
for i = 1 : m - 1
a(m, m) = a(m, m) - (a(m-1, i) * Rxx(m +1 - i)) / sigma2(m - 1);
end
for k = 1 : m -1
a(m, k) = a(m - 1, k) + a(m, m) * a(m - 1, m - k)'; % m阶AR模型中的m个系数中的除最后一个系数以外的系数
end
sigma2(m) = (1 - a(m, m) ^ 2) * sigma2(m - 1); % m阶AR模型当前对应的噪声功率
end
[H, w] = freqz(1, [1, a(p, :)], fs);
f = w / (2 * pi) * fs;
H = H * sigma2(m);
plot(f, abs(H).^2);
运行结果:
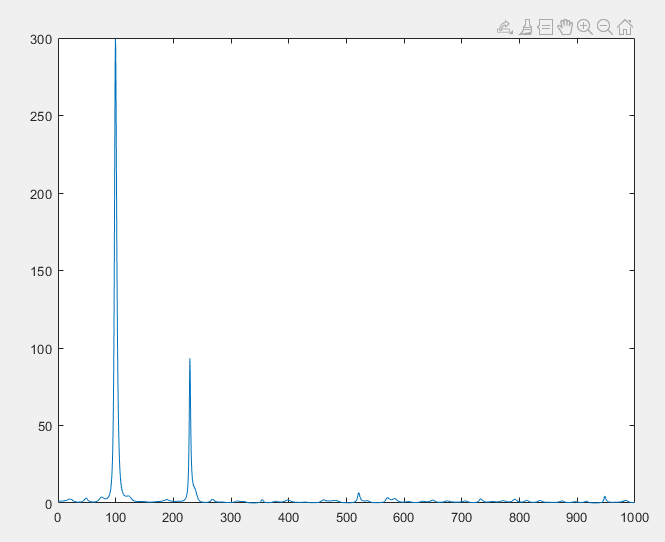
参考资料:
【1】 张贤达,现代信号处理,第3版
【2】 https://www.bilibili.com/video/BV1wS4y1D7ng/?p=1&vd_source=d7f21d136ca4d445e3fbba3c70c5c40e



 浙公网安备 33010602011771号
浙公网安备 33010602011771号