现代功率谱估计(3):SVD-TLS,奇异值分解—总体最小二乘方法求解AR模型参数
Yuler-Walker方程及修正Yuler-Walker方程
对于一个AR\((p)\)过程,其输出信号的自相关函数和AR系数有以下方程:
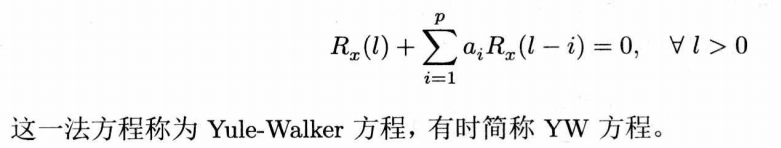
现在的问题是,如何求解AR模型的系数\(a_{i}\)以及AR模型的阶数\(p\),根据AR模型的参数可辨识性定理:

可以通过求解有限个(\(p\)个)修正Yuler-Walker方程来进行求解AR模型的系数\(a_{i}\),接下来的问题是:如何确定AR模型的合适的阶数\(p\),从而得知上面方程的个数?
为了解决这一问题我们先假设一个较大的AR模型的阶数\(pe\),在假设阶数为\(pe\)的情况下,上面的修正Yuler-Walker方程依旧成立:

其中上面在我们假设\(pe\),\(qe\)的情况下,\(pe,qe,M\)需要满足以下命题:

接下来就可以使用奇异值分解的方法,利用上面矩阵\(Re\)的奇异值来确定AR模型的真实阶数\(p\)
到这里先停一下,先放上具体的代码示例,动手将上面矩阵\(Re\)构建出来:
%% 根据样本序列估计的自相关生成矩阵Re
Rxx=xcorr(xn);
pe=100; % pe>=p;
qe=150; % qe>=q,(qe-pe)>=(q-p);
M=300; % M>=pe;
for i = 1 : N -1
Rx(i) = Rxx(N - 1 + i); % xcorr函数默认的自相关函数为最大值的点并非位于横坐标0处,此处将其平移到坐标轴处
end
Re=zeros(M,pe+1); % 书中p129, 4.4.23
for i=1:M
for j=1:(pe+1)
Re(i,j)=Rx(qe + i - j + 1);
end
end
上面生成的矩阵Re即为根据样本估计自相关得到的修正Yuler-Walker方程系数矩阵。
奇异值分解确定AR模型的阶数\(p\)
先对上面得到的样本估计相关函数矩阵\(Re\)做奇异值分解
再使用归一化奇异值的比值,设定合适的阈值来确定上面矩阵的有效秩\(p\),归一化奇异值定义为:
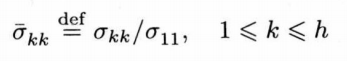
通过选择合适的阈值(一个接近于0的正数),并将大于此阈值的最大整数(奇异值个数)\(k\)取作矩阵\(Re\)的有效秩\(p\),即可得到一个相比于之前设定的\(pe\)更加合适的AR模型\(p\)。
这一段通过奇异值分解,根据奇异值的大小比较确定AR模型的阶数\(p\)的代码如下:
%% 根据前几个sigma的归一化比值,确定AR模型的阶数p
[U,S,V]=svd(Re); % 奇异值分解
%%求p值
p=0;
SS=zeros(1,pe+1)';
for i=1:(pe+1)
if S(i,i)/S(1,1)>0.05 % p132页4.4.40, 归一化比值,挑出前几个较大的奇异值,根据其个数确定阶数p
p=p+1;
if p>0
SS(p)=S(i,i);
end
end
end
总体最小二乘法(TLS)确定AR模型的参数
上面我们通过随机信号的样本信号估计出了修正Yuler-Walker方程的系数矩阵,通过奇异值分解,归一化比值和阈值比较之后确定了AR模型的阶数\(p\),接下来的问题就是如何求解修正Yuler-Walker方程中的未知数:
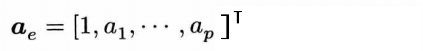
根据张贤达现代信号处理书上p135,式4.4.56,式4.4.58步骤:
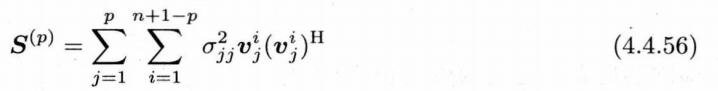
其中\(\sigma ^{2}_{jj]}\)为矩阵\(Re\)第\(j\)个奇异值的平方,向量\(v^{k}_{j}\)为矩阵\(Re\)奇异值分解之后的酉矩阵\(V\)的第\(j\)列的一个加窗段:
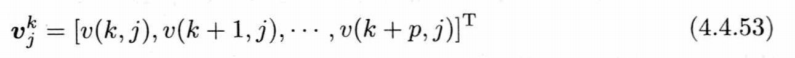
构造出矩阵\(S^{(p)}\)之后,即可求出上面解修正Yuler-Walker方程中的未知数。具体计算公式为:
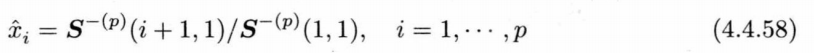
这一段根据矩阵\(Re\)奇异值分解之后的酉矩阵和相应奇异值构建矩阵\(S^{(p)}\)的代码如下:
[U, S, V] = svd( Re ); % 奇异值分解
%%求p值
p = 0;
SS=zeros(1, pe + 1)';
for i = 1 : ( pe + 1 )
if S(i , i) / S(1 , 1) > 0.05 % p132页4.4.40, 归一化比值,挑出前几个较大的奇异值,根据其个数确定阶数p
p = p + 1;
if p > 0
SS( p ) = S(i , i );
end
end
end
%% 求Sp及其逆
Sp = zeros( p + 1 , p + 1 );
for j = 1 : p
for i = 1 : (pe+1-p)
Sp = Sp + SS(j)^2 * V(i:i+p , j) * V( i : i+p , j )'; % p135 式4.4.58
end
end
至此,AR模型阶数\(p\)已确定,参数\(a_i\)也已求出,接下来可利用Cadzow谱估计子对功率谱进行估计(这部分代码以后再补上)
最后,给出汇总的实验仿真代码:
clc;
clear;
close all;
%% 参数设置
f1 = 70; f2 = 100; f3 = 120;
N = 1000;
fs = 512;
n = (1: 1000) * 1/ fs;
%% 仿真数据产生
xn = 2 * sin(2 * pi * f1 * n + pi / 3) + 2 * sin(2 * pi * f2 * n + pi / 4) + 2 * sin(2 * pi * f3 * n + pi / 5) ;
xn = xn + 2 * randn(size(n));
%% 根据样本序列估计的自相关生成矩阵Re
Rxx = xcorr(xn);
pe = 100; % pe>=p;
qe = 150; % qe>=q,(qe-pe)>=(q-p);
M = 300; % M>=pe;
for i = 1 : N -1
Rx(i) = Rxx(N - 1 + i); % xcorr函数默认的自相关函数为最大值的点并非位于横坐标0处,此处将其平移到坐标轴处
end
Re=zeros(M, pe+1); % 书中p129, 4.4.23
for i=1: M
for j=1: (pe+1)
Re(i, j)=Rx(qe + i - j + 1);
end
end
%% 根据前几个sigma的归一化比值,确定AR模型的阶数p
[U, S, V] = svd( Re ); % 奇异值分解
%%求p值
p = 0;
SS=zeros(1, pe + 1)';
for i = 1 : ( pe + 1 )
if S(i , i) / S(1 , 1) > 0.05 % p132页4.4.40, 归一化比值,挑出前几个较大的奇异值,根据其个数确定阶数p
p = p + 1;
if p > 0
SS( p ) = S(i , i );
end
end
end
%% 求Sp及其逆
Sp = zeros( p + 1 , p + 1 );
for j = 1 : p
for i = 1 : (pe+1-p)
Sp = Sp + SS(j)^2 * V(i:i+p , j) * V( i : i+p , j )'; % p135 式4.4.58
end
end
Sp_=inv(Sp);
%% 总体最小二乘估计
x=zeros(1,p+1)';
for i=1:(p+1)
x(i)=Sp_(i, 1)/ Sp_(1, 1); % p135 4.4.58
end
%% 求响应
a=x;
%% 随机信号的幅度谱
subplot 221
xfft = fft(xn);
freq = (1: length(xfft))/length(xfft) * fs;
f = freq(1:(length(xfft)/2 + 1));
plot(f, abs(xfft(1 : (length(xfft)/2)+1)));
title("原始信号的幅度谱")
%% AR模型的功率谱密度分布情况
[H, w] = freqz(1, a, fs);
subplot 222
plot(w/(2 * pi) * fs, abs(H).^2);
title("p阶AR模型的功率谱密度分布情况")
%% 周期图法
subplot 223
window=boxcar(length(xn));
nfft=fs;
[Pxx, w]=periodogram(xn,window,nfft,fs); %直接法
plot(w, Pxx)
title("直接周期图法计算随机信号Xn的功率谱密度分布")
运行结果:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号