现代功率谱估计（1）：求解Yuler-Walker方程的方法
相当多的平稳随机过程都可通过一个白噪声为输入，激励一个线性时不变系统来产生，此系统可用线性差分方程进行描述，此种差分方程即为自回归-滑动平均（autoregressive - moving average, AR-MA）模型。（张贤达，现代信号处理，P114）
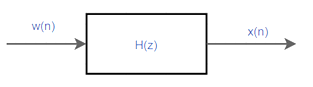
根据Wold分解定理（P118，定理4.2.4）：任何一个具有有限方差的ARMA或MA系统均可表示成唯一的AR过程。
下面通过求解相应的AR过程的系数的方式来求解一个采样信号序列的功率谱密度估计。
AR模型:
AR模型的系统差分方程为：
AR模型的系统函数为：
根据卷积相关定理，若AR系统的系统冲激响应为\(h(n)\)， 则系统输出\(y(n)\) 和系统输入\(x(n)\)的关系为：
根据相关卷积定理：\(x(n)\)和\(h(n)\)的卷积之后的自相关，等于\(x(n)\)的自相关和\(h(n)\) 的自相关的卷积。
故有：
其中\(m\)为相关计算过程中的时间差。
根据具有随机输入的线性系统的输入信号与输出信号的功率谱之间的关系（P17页，式1.4.10）：
故一旦确定AR模型的系数\(a_i\) ，则AR模型的系统函数可以确定；如果假设输入AR系统的白噪声方差为1，则AR系统的功率谱密度分布可知。
由上面的4.2.7式，可将系统的输出\(x(n)\)表示为：
即通过n时刻之前的\(p\)个时刻的系统输出信号的线性组合来对\(n\)时刻的系统输出进行预测，预测过程中的误差为\(e(n)\)。
预测过程中的均方误差为：
要想使得预测过程中的均方误差值\(E[e^{2}(n)]\)最小，则AR系统的参数\(a_{i}\)的选择应该使得下式成立：
即：
即可得到关于AR系数\(a_{i}\)的方程：
将上面等式写成矩阵形式为：
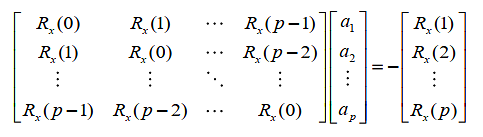
令矩阵\(R\)为：
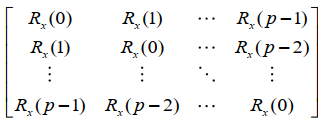
右边常数项\(b\)为:
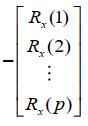
则AR模型的系数\(a_{i}\) 组成的向量也就是上面Yuler-Walker方程的解为：
输入的白噪声的方差
输入AR系统的白噪声信号用\(v(n)\)表示，输出AR系统的随机过程用\(u(n)\)表示，则AR过程表示为：
两边同时乘以\(u^{*}(n-l)\)，则上式变为：
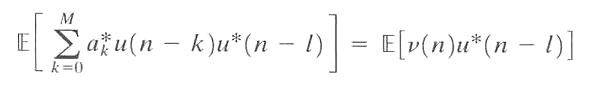
当取\(l=0\)时，上式右边变为：
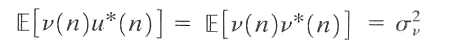
则可得到白噪声方差的计算公式：
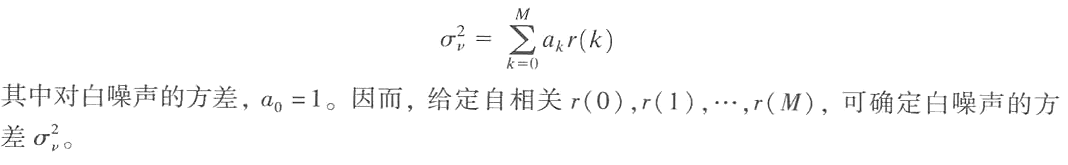
matlab代码如下：
%% yule_walker 方程的随机信号功率谱估计
clc; clear; close all;
f1 = 100; f2 = 230 ;
fs = 2000;
N = 256; % 信号长度
p = 100; % AR模型的阶数
n = (1 : N) * 1 /fs ; % 采样时间点
wn = randn(1, N);
xn = 2 * sin(2 * pi * f1 * n + pi / 3) + sin(2 * pi * f2 * n + pi / 4) + wn;
Rxx = xcorr(xn, 'biased');
Rx = zeros(1, p + 1); % Rx(0)，Rx(1), Rx(2), ........Rx(p)共p + 1个数
for i = 1 : p+1
Rx(i) = Rxx(N + i - 1);
% xn的自相关函数图像中时间差值为0的点的横坐标并不是位于横坐标0处，需要进行搬移
end
R = zeros(p, p);
a = zeros(p, 1);
b = zeros(p, 1);
for i = 1: p
for j = 1: p
R(i, j) = Rx(abs(i - j) + 1); % YW方程的系数矩阵
end
end
for k = 1: p
b(k, 1) = -1 * Rx(k + 1); % YW方程右边的常数向量
end
a = R\b; % YW方程的解
a = a'; % AR模型的系数a（i）
%% 求白噪声的方差
sigma2 = 0;
sigma2 = sigma2 + 1 * Rx(1); % a0=1
for i = 1 : length(a)
sigma2 = sigma2 + a(i) * Rx(i + 1);
end
[H, w] = freqz(1, [1, a], N);
Sxx =sigma2 * abs(H) .^2; % 此处输入系统的高斯白噪声功率视为1
f = w/(2 * pi) * fs;
subplot 121
plot(f, Sxx);
title("Yuler-Walker方程求解AR系数功率谱估计")
%% 周期图法功率谱估计
win = boxcar(N);
nfft = fs;
[Sxx2, f] = periodogram(xn, win, nfft, fs);
subplot 122
plot(f, Sxx2)
title("周期图法功率谱估计")
运行结果：
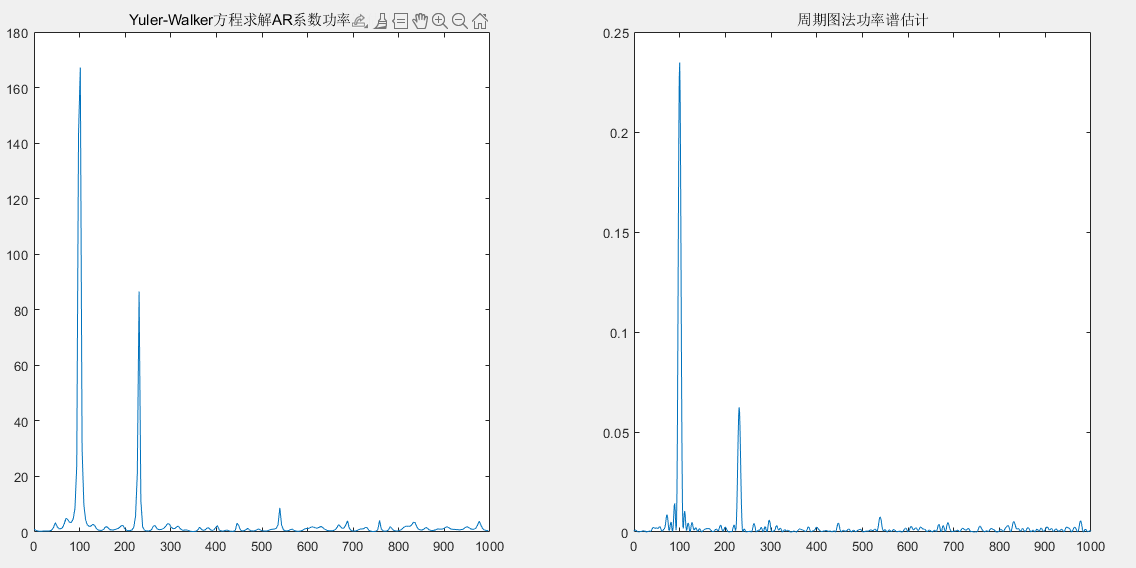
直接求解Yuler-Walker方程，求解AR模型的系数进而估计功率谱的方法的缺点是，AR模型的阶数未进行可靠的确定，根据张贤达现代信号处理p131页所说：
如果要进行确定阶数的AR模型的求解，应该在考虑系统扰动的同时，使用奇异值分解的方法确定AR模型的阶数，再综合考虑系数矩阵（根据样本估计的相关矩阵）的误差，采用总体最小二乘法，求解修正的Yuler-Walker方程。
