神经网络（NN）的复杂度
空间复杂度：
计算神经网络的层数时只统计有运算能力的层，输入层仅仅起到将数据传输进来的作用，没有涉及到运算，所以统计神经网络层数时不算输入层
输入层和输出层之间所有层都叫做隐藏层
层数 = 隐藏层的层数 + 1个输出层
总参数个数 = 总w个数 + 总b个数
时间复杂度：
乘加运算次数
学习率以及参数的更新：
\[{w_{t + 1}} = {w_t} - lr*\frac{{\partial loss}}{{\partial {w_t}}}
\]
指数衰减学习率的选择及设置
可以先用较大的学习率，快速得到较优解，然后逐步减小学习率，使模型在训练后期稳定。
指数衰减学习率 = 初始学习率 * 学习率衰减率（ 当前轮数 / 多少轮衰减一次 ）
\[指数衰减学习率 = 初始学习率*{学习率衰减率^{\frac{当前轮数}{多少轮衰减一次}}}
\]
#学习率衰减
import tensorflow as tf
w = tf.Variable(tf.constant(5, dtype=tf.float32))
epoch = 40
LR_BASE = 0.2
LR_DECAY = 0.99
LR_STEP = 1
for epoch in range(epoch):
lr = LR_BASE * LR_DECAY**(epoch / LR_STEP)
with tf.GradientTape() as tape:
loss = tf.square(w + 1)
grads = tape.gradient(loss, w)
w.assign_sub(lr * grads)
print("After %2s epoch,\tw is %f,\tloss is %f\tlr is %f" % (epoch, w.numpy(), loss,lr))
After 0 epoch, w is 2.600000, loss is 36.000000 lr is 0.200000
After 1 epoch, w is 1.174400, loss is 12.959999 lr is 0.198000
After 2 epoch, w is 0.321948, loss is 4.728015 lr is 0.196020
After 3 epoch, w is -0.191126, loss is 1.747547 lr is 0.194060
After 4 epoch, w is -0.501926, loss is 0.654277 lr is 0.192119
After 5 epoch, w is -0.691392, loss is 0.248077 lr is 0.190198
After 6 epoch, w is -0.807611, loss is 0.095239 lr is 0.188296
After 7 epoch, w is -0.879339, loss is 0.037014 lr is 0.186413
After 8 epoch, w is -0.923874, loss is 0.014559 lr is 0.184549
After 9 epoch, w is -0.951691, loss is 0.005795 lr is 0.182703
After 10 epoch, w is -0.969167, loss is 0.002334 lr is 0.180876
After 11 epoch, w is -0.980209, loss is 0.000951 lr is 0.179068
After 12 epoch, w is -0.987226, loss is 0.000392 lr is 0.177277
After 13 epoch, w is -0.991710, loss is 0.000163 lr is 0.175504
After 14 epoch, w is -0.994591, loss is 0.000069 lr is 0.173749
After 15 epoch, w is -0.996452, loss is 0.000029 lr is 0.172012
After 16 epoch, w is -0.997660, loss is 0.000013 lr is 0.170292
After 17 epoch, w is -0.998449, loss is 0.000005 lr is 0.168589
After 18 epoch, w is -0.998967, loss is 0.000002 lr is 0.166903
After 19 epoch, w is -0.999308, loss is 0.000001 lr is 0.165234
After 20 epoch, w is -0.999535, loss is 0.000000 lr is 0.163581
After 21 epoch, w is -0.999685, loss is 0.000000 lr is 0.161946
After 22 epoch, w is -0.999786, loss is 0.000000 lr is 0.160326
After 23 epoch, w is -0.999854, loss is 0.000000 lr is 0.158723
After 24 epoch, w is -0.999900, loss is 0.000000 lr is 0.157136
After 25 epoch, w is -0.999931, loss is 0.000000 lr is 0.155564
After 26 epoch, w is -0.999952, loss is 0.000000 lr is 0.154009
After 27 epoch, w is -0.999967, loss is 0.000000 lr is 0.152469
After 28 epoch, w is -0.999977, loss is 0.000000 lr is 0.150944
After 29 epoch, w is -0.999984, loss is 0.000000 lr is 0.149434
After 30 epoch, w is -0.999989, loss is 0.000000 lr is 0.147940
After 31 epoch, w is -0.999992, loss is 0.000000 lr is 0.146461
After 32 epoch, w is -0.999994, loss is 0.000000 lr is 0.144996
After 33 epoch, w is -0.999996, loss is 0.000000 lr is 0.143546
After 34 epoch, w is -0.999997, loss is 0.000000 lr is 0.142111
After 35 epoch, w is -0.999998, loss is 0.000000 lr is 0.140690
After 36 epoch, w is -0.999999, loss is 0.000000 lr is 0.139283
After 37 epoch, w is -0.999999, loss is 0.000000 lr is 0.137890
After 38 epoch, w is -0.999999, loss is 0.000000 lr is 0.136511
After 39 epoch, w is -0.999999, loss is 0.000000 lr is 0.135146
激活函数
sigmoid函数
tf.nn. sigmoid(x)
\[f(x) = \frac{1}{{1 + {e^{ - x}}}}
\]
图像：
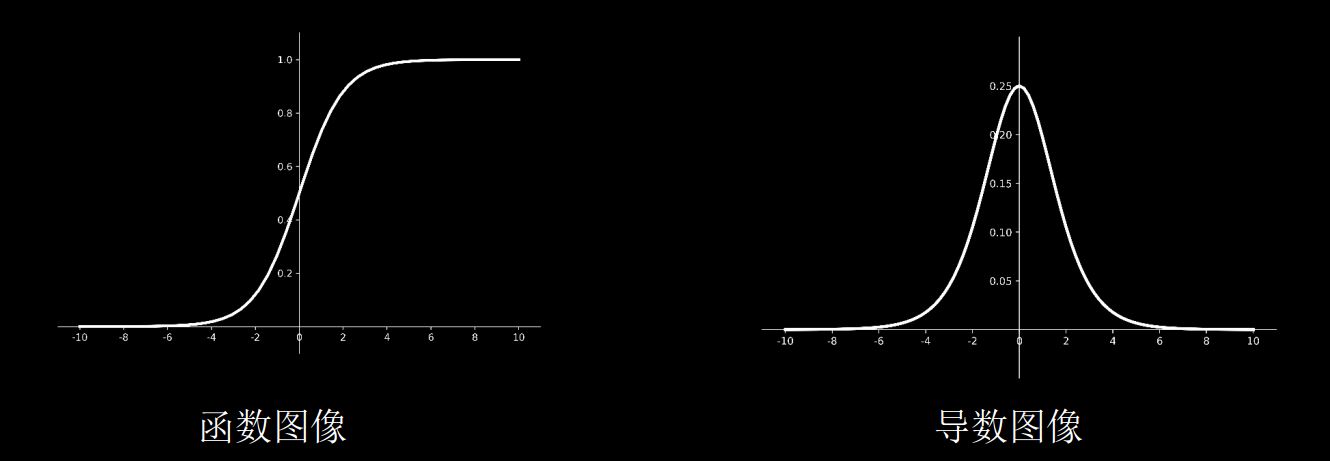
相当于对输入进行了归一化
- 多层神经网络更新参数时，需要从输出层往输入层方向逐层进行链式求导，而sigmoid函数的导数输出是0到0.25之间的小数，链式求导时，多层导数连续相乘会出现多个0到0.25之间的值连续相乘，结果将趋近于0，产生梯度消失，使得参数无法继续更新
- 且sigmoid函数存在幂运算，计算比较复杂
tanh函数
tf.math. tanh(x)
\[f(x) = \frac{{1 - {e^{ - 2x}}}}{{1 + {e^{ - 2x}}}}
\]
图像：
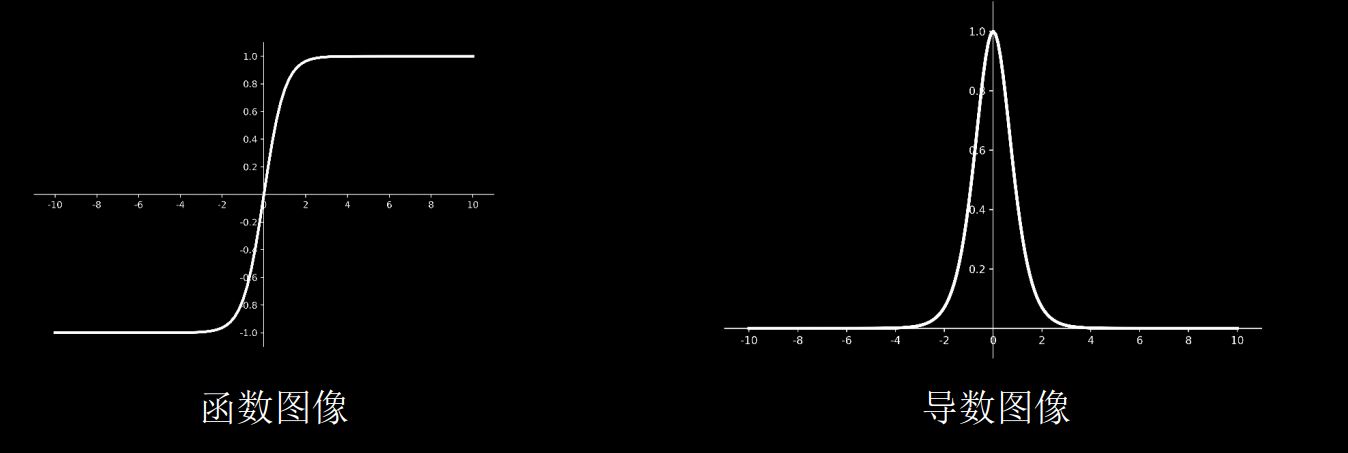
和上面提到的sigmoid函数一样，同样存在梯度消失和幂运算复杂的缺点
Relu函数
tf.nn.relu(x)
\[f(x)=max(x,0)=0(x<0)时或者x(x>=0)时
\]
图像：
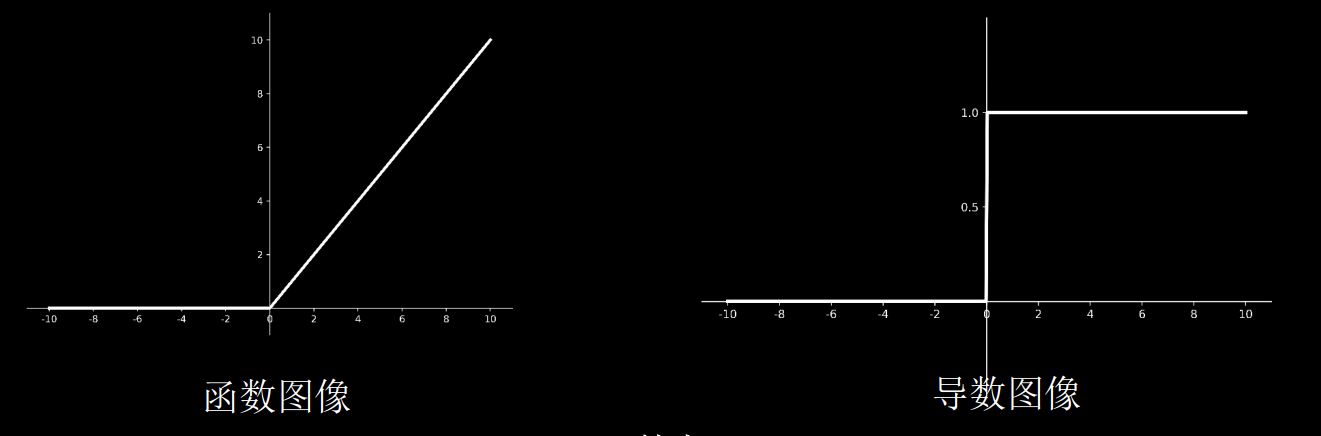
- Relu函数在正区间内解决了梯度消失的问题，使用时只需要判断输入是否大于0，计算速度快
- 训练参数时的收敛速度要快于sigmoid函数和tanh函数
- 输出非0均值，收敛慢
- Dead RelU问题：送入激活函数的输入特征是负数时，激活函数输出是0，反向传播得到的梯度是0，致使参数无法更新，某些神经元可能永远不会被激活。但是可以通过改进随机初始化，避免过多的负数特征送入Relu函数，可以通过设置更小的学习率来减小参数分布的巨大变化，来避免训练过程中产生过多负数特征。
Leaky Relu函数
tf.nn.leaky_relu(x)
\[𝒇(𝒙) = max(𝜶𝒙, 𝒙)
\]
图像：
Leaky Relu函数是为了解决负数输入特征引起含Relu激活函数的神经元死亡的问题提出的，引入负区间固定斜率𝜶，
对于初学者的建议：
首选relu激活函数；
学习率设置较小值；
输入特征标准化，即让输入特征满足以0为均值，1为标准差的正态分布；
初始参数中心化，即让随机生成的参数满足以0为均值， $\sqrt {\frac{2}{{\text{当前层的输入特征个数}}}} $为标准差的正态分布。
损失函数
前向传播计算出的预测值（y）与已知标准答案（y_）的差距
神经网络的优化目标就是找到某一组参数，使得计算出来的结果y和已知标准答案y_最为接近，即loss值最小
主流损失函数loss有3种计算方法
- 均方误差mse(Mean Squared Error)
- 自定义
- 交叉熵ce(Cross Entropy)
均方误差mse(Mean Squared Error):
\[MSE(y,y\_) = \frac{{\sum\limits_{i = 1}^n {{{(y - y\_)}^2}} }}{n}
\]
TensorFlow实现：
loss_mse = tf.reduce_mean(tf.square(y_ - y))
例子：预测酸奶日销量数
酸奶日销量为y，由x1、x2两个影响日销量的因素所影响
标准答案为y_=x1+x2
现在自造数据集，随机的x1和x2，为了更真实，x1和x2求和后再给y_加入-0.05至+0.05的随机噪声
构建1层的神经网络，预测酸奶日销量
import tensorflow as tf
import numpy as np
SEED = 23455
rdm = np.random.RandomState(seed=SEED) # 生成[0,1)之间的随机数
x = rdm.rand(32, 2) #生成32行2列的输入特征x，包含32组0到1之间的随机数x1和x2
y_ = [[x1 + x2 + (rdm.rand() / 10.0 - 0.05)] for (x1, x2) in x]
# 取出每组的x1和x2相加，再加上随机噪声，构建出标准答案y_
# 生成噪声[0,1)之间的随机数，再除以10变成[0,0.1)之间的随机数，再减去0.05变成[-0.05,0.05)之间的随机随机噪声
x = tf.cast(x, dtype=tf.float32)
# x转变数据类型
w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1))
# 随机初始化参数w1，初始化为2行1列
epoch = 15000 # 数据集迭代15000次
lr = 0.002
for epoch in range(epoch):
#for循环中用with结构，用前向传播计算结果y
with tf.GradientTape() as tape:
y = tf.matmul(x, w1)
loss_mse = tf.reduce_mean(tf.square(y_ - y)) # 求均方误差损失函数
grads = tape.gradient(loss_mse, w1) # 损失函数对待训练的参数w1求偏导
w1.assign_sub(lr * grads) # 更新参数w1
if epoch % 500 == 0:
print("After %d training steps,w1 is " % (epoch))
print(w1.numpy(), "\n")
# 每迭代500轮打印当前的参数w1
print("Final w1 is: ", w1.numpy())
After 0 training steps,w1 is
[[-0.8096241]
[ 1.4855157]]
After 500 training steps,w1 is
[[-0.21934733]
[ 1.6984866 ]]
After 1000 training steps,w1 is
[[0.0893971]
[1.673225 ]]
After 1500 training steps,w1 is
[[0.28368822]
[1.5853055 ]]
After 2000 training steps,w1 is
[[0.423243 ]
[1.4906037]]
After 2500 training steps,w1 is
[[0.531055 ]
[1.4053345]]
After 3000 training steps,w1 is
[[0.61725086]
[1.332841 ]]
After 3500 training steps,w1 is
[[0.687201 ]
[1.2725208]]
After 4000 training steps,w1 is
[[0.7443262]
[1.2227542]]
After 4500 training steps,w1 is
[[0.7910986]
[1.1818361]]
After 5000 training steps,w1 is
[[0.82943517]
[1.1482395 ]]
After 5500 training steps,w1 is
[[0.860872 ]
[1.1206709]]
After 6000 training steps,w1 is
[[0.88665503]
[1.098054 ]]
After 6500 training steps,w1 is
[[0.90780276]
[1.0795006 ]]
After 7000 training steps,w1 is
[[0.92514884]
[1.0642821 ]]
After 7500 training steps,w1 is
[[0.93937725]
[1.0517985 ]]
After 8000 training steps,w1 is
[[0.951048]
[1.041559]]
After 8500 training steps,w1 is
[[0.96062106]
[1.0331597 ]]
After 9000 training steps,w1 is
[[0.9684733]
[1.0262702]]
After 9500 training steps,w1 is
[[0.97491425]
[1.0206193 ]]
After 10000 training steps,w1 is
[[0.9801975]
[1.0159837]]
After 10500 training steps,w1 is
[[0.9845312]
[1.0121814]]
After 11000 training steps,w1 is
[[0.9880858]
[1.0090628]]
After 11500 training steps,w1 is
[[0.99100184]
[1.0065047 ]]
After 12000 training steps,w1 is
[[0.9933934]
[1.0044063]]
After 12500 training steps,w1 is
[[0.9953551]
[1.0026854]]
After 13000 training steps,w1 is
[[0.99696386]
[1.0012728 ]]
After 13500 training steps,w1 is
[[0.9982835]
[1.0001147]]
After 14000 training steps,w1 is
[[0.9993659]
[0.999166 ]]
After 14500 training steps,w1 is
[[1.0002553 ]
[0.99838644]]
Final w1 is: [[1.0009792]
[0.9977485]]
最后得到结果w1所表示的两个参数分别为
[[1.0009792] [0.9977485]]
与标准答案所给出的y_=x1+x2很接近
上面所使用的均方误差损失函数
\[MSE(y,y\_) = \frac{{\sum\limits_{i = 1}^n {{{(y - y\_)}^2}} }}{n}
\]
默认认为销量预测多了或者预测少了，损失是一样的
然而，在真实情况中，
- 如果预测多了，也就是没有卖完，这时候损失的是成本
- 如果预测少了，也就是不够卖，该赚到的钱没有赚到，这时候损失的是利润
利润和成本往往不相等
下面使用自定义的损失函数
\[预测的结果y偏小，损失的是利润（PROFIT）
\]
\[f(y,y_)=PROFIT*(y_{-}-y)
\]
\[预测的结果y偏大，损失的是成本（COST）
\]
\[f(y,y_)=COST*(y-y_{-})
\]
loss_zdy = tf.reduce_sun((tf.where(y,y_),COST(y-y_),PROFIT(y_,y)))
预测酸奶销量，酸奶成本（COST）1元，酸奶利润（PROFIT）99元。
- 预测少了损失利润99元，
- 预测多了损失成本1元。
预测少了损失大，希望生成的预测函数往多了预测。
# 自定义损失函数
import tensorflow as tf
import numpy as np
SEED = 23455
COST = 1
PROFIT = 99
rdm = np.random.RandomState(SEED)
x = rdm.rand(32, 2)
y_ = [[x1 + x2 + (rdm.rand() / 10.0 - 0.05)] for (x1, x2) in x]
x = tf.cast(x, dtype=tf.float32)
w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1))
epoch = 10000
lr = 0.002
for epoch in range(epoch):
with tf.GradientTape() as tape:
y = tf.matmul(x, w1)
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_) * COST, (y_ - y) * PROFIT))
# 相比上面使用均方误差损失函数，只改动了这里，使用自定义的损失函数
grads = tape.gradient(loss, w1)
w1.assign_sub(lr * grads)
if epoch % 500 == 0:
print("After %d training steps,w1 is " % (epoch))
print(w1.numpy(), "\n")
print("Final w1 is: ", w1.numpy())
After 0 training steps,w1 is
[[2.8786578]
[3.2517848]]
After 500 training steps,w1 is
[[1.1460369]
[1.0672572]]
After 1000 training steps,w1 is
[[1.1364173]
[1.0985414]]
After 1500 training steps,w1 is
[[1.1267972]
[1.1298251]]
After 2000 training steps,w1 is
[[1.1758107]
[1.1724023]]
After 2500 training steps,w1 is
[[1.1453722]
[1.0272155]]
After 3000 training steps,w1 is
[[1.1357522]
[1.0584993]]
After 3500 training steps,w1 is
[[1.1261321]
[1.0897831]]
After 4000 training steps,w1 is
[[1.1751455]
[1.1323601]]
After 4500 training steps,w1 is
[[1.1655253]
[1.1636437]]
After 5000 training steps,w1 is
[[1.1350871]
[1.0184573]]
After 5500 training steps,w1 is
[[1.1254673]
[1.0497413]]
After 6000 training steps,w1 is
[[1.1158477]
[1.0810255]]
After 6500 training steps,w1 is
[[1.1062276]
[1.1123092]]
After 7000 training steps,w1 is
[[1.1552413]
[1.1548865]]
After 7500 training steps,w1 is
[[1.1248026]
[1.0096996]]
After 8000 training steps,w1 is
[[1.1151826]
[1.0409834]]
After 8500 training steps,w1 is
[[1.1055626]
[1.0722672]]
After 9000 training steps,w1 is
[[1.1545763]
[1.1148446]]
After 9500 training steps,w1 is
[[1.144956]
[1.146128]]
Final w1 is: [[1.1255957]
[1.0237043]]
最后得到的w1，w2为
[[1.1255957]
[1.0237043]]
均大于1，所得结果确实是朝着使y尽量大的方向预测，以减少损失函数
当将酸奶成本改成99，利润改成1
最后得到的w1，w2为
Final w1 is: [[0.9205433]
[0.9186459]]
均小于1，所得结果确实是朝着使y尽量小的方向预测，以减少损失函数
交叉熵CE（Cross Entropy）
交叉熵损失函数CE (Cross Entropy)：表征两个概率分布之间的距离
- 交叉熵越大，两个概率分布的距离越远
- 交叉熵越小，两个概率分布的距离越近
\[H(y\_,y) = - \sum\limits_{}^{} {(y\_*\ln y)} \
\]
tf.losses.categorical_crossentropy(y_，y)
其中y_表示标准答案的概率分布
y表示预测结果的概率分布
# 交叉熵
import tensorflow as tf
loss_ce1 = tf.losses.categorical_crossentropy([1, 0], [0.6, 0.4])
loss_ce2 = tf.losses.categorical_crossentropy([1, 0], [0.8, 0.2])
print("loss_ce1:", loss_ce1)
print("loss_ce2:", loss_ce2)
loss_ce1: tf.Tensor(0.5108256, shape=(), dtype=float32)
loss_ce2: tf.Tensor(0.22314353, shape=(), dtype=float)
在执行分类问题时通常，使用softmax函数和交叉熵相结合
输出先过softmax函数，让输出结果符合概率分布，再计算y与y_的交叉熵损失函数。
TensoFlow给出了可以同时计算概率分布和交叉熵得函数为：
tf.nn.softmax_cross_entropy_with_logits(y_，y)
# softmax和交叉熵函数
y_ = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 0, 0], [0, 1, 0]])
y = np.array([[12, 3, 2], [3, 10, 1], [1, 2, 5], [4, 6.5, 1.2], [3, 6, 1]])
y_pro = tf.nn.softmax(y) # 语句1
loss_ce1 = tf.losses.categorical_crossentropy(y_,y_pro) # 语句2
loss_ce2 = tf.nn.softmax_cross_entropy_with_logits(y_, y) # 这一句可以同时执行上面的语句1和语句2
print('分步计算的结果:\n', loss_ce1)
print('结合计算的结果:\n', loss_ce2)
分步计算的结果:
tf.Tensor(
[1.68795487e-04 1.03475622e-03 6.58839038e-02 2.58349207e+00
5.49852354e-02], shape=(5,), dtype=float64)
结合计算的结果:
tf.Tensor(
[1.68795487e-04 1.03475622e-03 6.58839038e-02 2.58349207e+00
5.49852354e-02], shape=(5,), dtype=float64)
