梯度下降

成本函数（Cost function）：

\[J(w,b) = \frac{1}{m}\sum\limits_{i = 1}^m {L({{\widehat y}^{(i)}},{y^{(i)}})} = - \frac{1}{m}\sum\limits_{i = 1}^m {\left[ {{y^{(i)}}*\log ({{\widehat y}^{(i)}}) + (1 - {y^{(i)}})*\log (1 - {{\widehat y}^{(i)}})} \right]} \]

衡量的是参数\(w\)和\(b\)在训练集上的效果

成本函数是一个在三维空间上的凹函数，

梯度下降就是，从\(w\)和\(b\)的初始值开始，朝着能使成本函数\(J(w,b)\)下降最快的方向移动一步，

\(J(w,b)\)下降之后，再让\(w\)和\(b\)向前走一步，即为梯度下降的一次迭代

梯度下降（Gradient descent）

本来\(J(w,b)\)由\(w\)和\(b\)两位参数决定取值，现在忽略一个参数，使\(J(w)\)仅有\(w\)为自变量，图解其梯度下降过程如下：

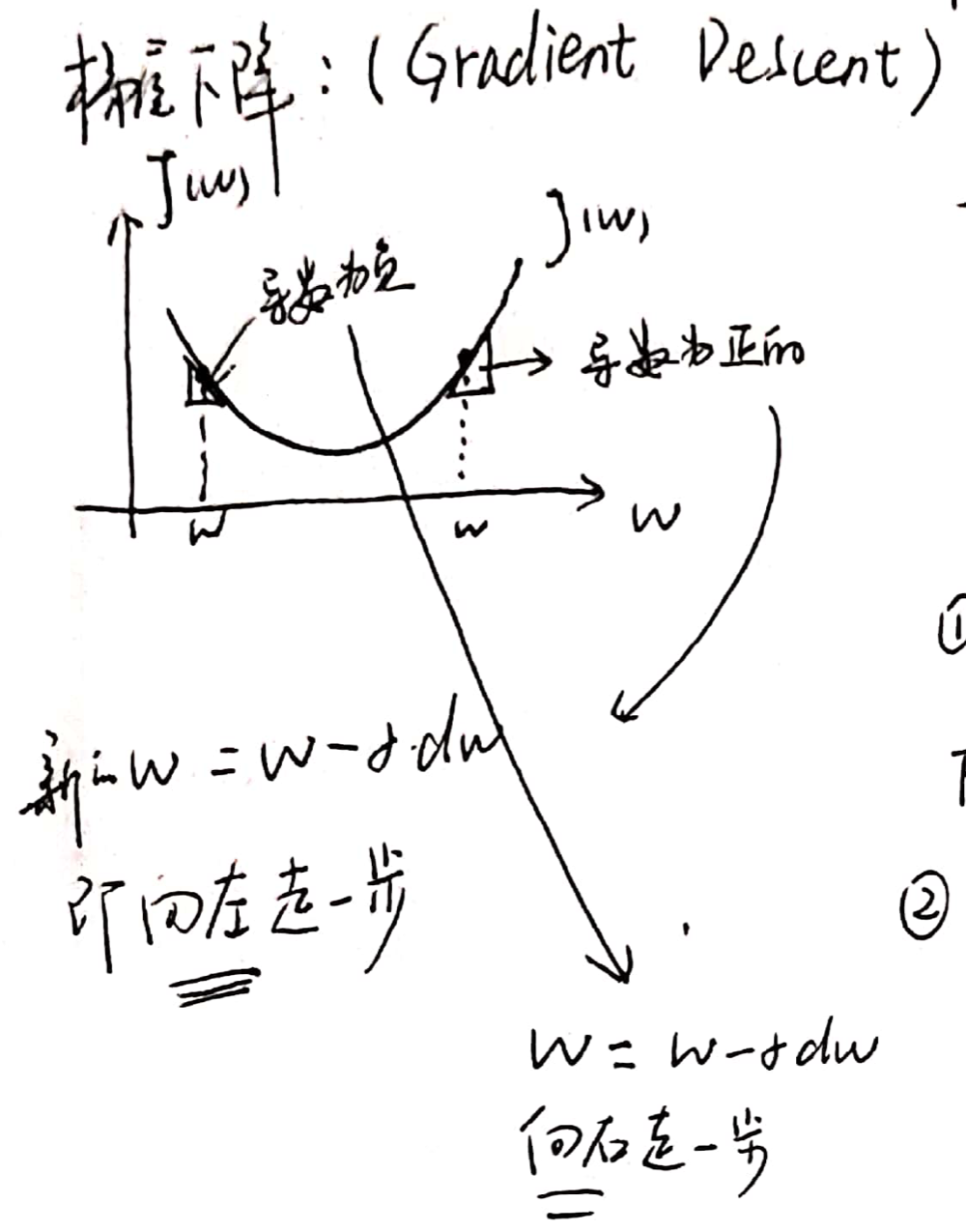
梯度下降的过程：

\[w: = w - \alpha \frac{{dJ(w)}}{{dw}} \]

其中：

  • $\alpha $表示学习率，通过控制学习率的大小可以控制每一次迭代或者梯度下降的步长，以后会提到如何选择学习率
  • \(\frac{{dJ(w)}}{{dw}}\)表示\(J(w)\)对\(w\)的导数，在Python编程过程中用dw表示
  • ":="表示更新前面的\(w\)的值

现在回到两个自变量\(w\)和\(b\)的情况，在logstic回归过程中，成本函数\(J(w,b)\)是\(w\)和\(b\)的函数

在这种情况下，梯度下降过程就由上面的只更新一个参数\(w\)变成要更新两个参数\(w\)和\(b\)的情况了，而每一次梯度下降也变成由更新\(w\)和更新\(b\)的两部分组成，而上面的求导过程也变成了求偏导过程，如下：

\[w: = w - \alpha \frac{{\partial J(w,b)}}{{\partial w}} \]

\[b: = b - \alpha \frac{{\partial J(w,b)}}{{\partial b}} \]

具体编程时，\(\frac{{\partial J(w,b)}}{\partial {w}}\)用dw表示，\(\frac{{\partial J(w,b)}}{\partial {b}}\)用db表示

前缀d表示输出变量对某个参数的导数，用d(var)表示，\(d(var)= \frac{{\partial J(w,b)}}{{\partial (var)}}\)

dv，da，db，dl均表示最终变量对各个自变量的导数，或者说是偏导数

logistic回归的前向传播和反向传播过程

logistic前向传播的输出为$a = {\widehat y} $,

\[z = {w^T}x + b \]

\[{\widehat y}=a=\sigma (z) \]

\[a = {\widehat y} = - [y*\log (a) + (1 - y)*\log (1 - a)] \]

假设样本只有x1和x2两个输入特征，则前向传播和反向传播求导的示意如下：

在logstic回归中我们要做的就是利用梯度下降不断的更新迭代\(w\)和\(b\)的值，来使得损失函数\(L(a,y)\)最小

所以我们要做的是，首先计算损失函数对各个参数的导数，或者说是偏导数，然后利用梯度下降不断的更新迭代\(w\)和\(b\)的值：

计算dz：dz=a-y

计算dw1：dw1=x1*dz

计算dw2：dw2=x2*dz

计算db：db=dz

然后是梯度下降迭代过程：
更新w1为：w1=w1-$\alpha $*dw1

更新w2为：w2=w2-$\alpha $*dw2

更新b为：b=b-$\alpha $*db

其中$\alpha $为学习率

上面就是单个样本的一次梯度更新步骤，实现单个训练样本的logistic回归的梯度下降法

全局的梯度下降法

上面提到的是单个样本的梯度下降过程，下面将这个范围拓展到全局

成本函数\(J(w,b)\):

\[J(w,b) = \frac{1}{m}\sum\limits_{i = 1}^m {L({a^{(i)}},{y^{(i)}})} \]

其中：

\[{a^{(i)}} = {{\hat y}^{(i)}} = \sigma ({z^{(i)}}) = \sigma ({w^T}{x^{(i)}} + b) \]

则

\[\frac{{\partial J(w,b)}}{{\partial {w_1}}} = \frac{1}{m}\sum\limits_{i = 1}^m {\frac{{\partial L({a^{(i)}},{y^{(i)}})}}{{\partial {w_1}}}} \]

上标（i）表示这是对第i个训练样本的计算，下面的计算过程为 :

上面的计算过程可以计算出成本函数\(J(w,b)\)对w1，w2和b的导数

dw1，dw2等于全局成本函数对w1，w2的导数，其中dw1，dw2没有上标（i）这是因为其作为累加器，求取的是整个训练集上的和，而dz则是相对于单个训练样本而言的。

完成上述计算后再进行梯度下降的迭代更新：

\[{w_1}: = {w_1} - \alpha d{w_1} \]

\[{w_2}: = {w_2} - \alpha d{w_2} \]

\[{b}: = {b} - \alpha d{b} \]

而在实际的计算机处理过程中，上面提到的使用两个for循环的方法过于低效，所以我们接下来采用将各个参数向量化的方法来取代for循环