Logistic Regression （逻辑回归）：用于二分分类的算法。

例如：

判断一幅图片是否为猫的图片，结果有两种:1（是猫）和0（不是猫）

假设输入的图片由64*64个像素组成，每个像素包含RGB三种不同的颜色分量，

则每一幅图片作为一个输入\(x^{(i)}\) 其中包含的输入特征的个数为64x64x3 ,将输入特征的个数记作\(n_{x}\)

如何通过输入的\(x^{(i)}\) ,来判断对应的结果\(y^{(i)}\)是(\(y^{(i)}=1\))或者不是(\(y^{(i)}=0\))为猫图片？

\((x,y)\)是表示一个单独的样本，其中\(x\) 是\(n_x\) 维的特征向量，\(y\)则表示最终判断的结果，\(y\) 只有两种情况： \(y=0\) 或者 \(y=1\) .

训练集\(x\) 由m个训练样本组成

\((x_1，y_1）\) 表示样本1的输入和输出

\((x_2，y_2)\) 表示样本2的输入和输出

……………………

\((x_m，y_m)\) 表示样本m的输入和输出

m表示训练样本的个数，

定义\(X\)由训练集中的\(x^{(1)}，x^{(2)}，……，x^{(m)}\) 表示：

\[X = \left( {\begin{array}{*{20}{c}} \vdots & \vdots & \vdots \\ {{x^{(1)}}}& \cdots &{{x^{(m)}}} \\ \vdots & \vdots & \vdots \end{array}} \right) \]

向量\(X\) 有m列（训练集的样本个数），\(n_x\)行

输出用\(Y\)表示：

\[Y=[y^{(1)},y^{(2)}.....,y^{(m)}] \]

\(Y\)是\(1*m\) 的矩阵。

在监督学习问题中，输出\(y\) 的标签是0或者1时，这是一个二元分类的问题。

输入\(x\) 有可能是一张图，

输入\(x\) ，得到\(y\)，\(\widehat y\)表示对结果\(y\) 的预测，确切的说\(\widehat y\) 表示一个概率，

\[\widehat y=P(y=1|_{x}) \]

当输入为一张猫的图片时，\(\widehat y\) 告诉你这是一张猫的图片的概率

Logistic回归的参数

线性回归：\(\widehat y=w^{T}x+b\)

但是我们期望得到的\(\widehat y\) 应该表示的是一个概率，\(\widehat y\) 应该介于\(0 \sim 1\) 之间，

所以在Logistic回归中，应该将输出变成

\[\widehat y=Sigmoid(w^{T}x+b) \]

\(Sigmoid(z)\)函数的图形：

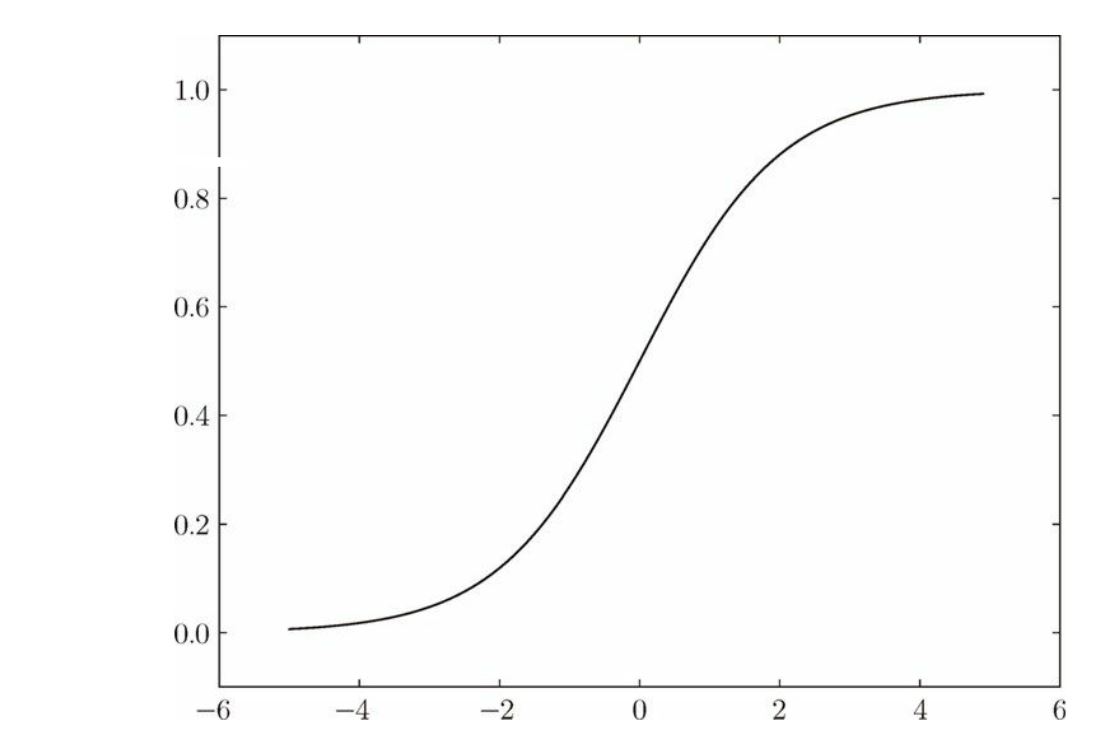
其中

\[z=w^{T}x+b \]

\[\sigma \left( z \right) = Sigmoid(z) = \frac{1}{{1 + {e^{ - z}}}} \]

当\(z \to \infty\)和\(z \to 0\)时：

\[z \to \infty , e^{-z} \to 0 ,\sigma(z) \to 1 \]

\[z \to -\infty , e^{-z} \to \infty ,\sigma(z) \to 0 \]

学习Logistic回归，也就是学习参数\(w\) 和参数\(b\)

定义一个成本函数（Cost function）

我们给出一个训练集：

\[\{ ({x^{(1)}},{y^{(1)}}).({x^{(2)}},{y^{(2)}}).......({x^{(m)}},{y^{(m)}}).\} \]

通过在训练集中的一系列操作，找到\(w\) 和\(b\) ,使得

希望得到的输出为：

\[{\widehat y^{(i)}} \approx {y^{(i)}} \]

其中对于训练样本\((i)\) ,对应的预测值为\({\widehat y^{(i)}}\)

\[{\widehat y^{(i)}} =Sigmoid(z^{(i)})=Sigmoid(w^{T}x^{(i)}+b) \]

损失函数（Loss function）:用来衡量算法的运行情况，

通过定义损失函数\(L(\widehat y,y)\) 来衡量预测输出值 \(\widehat y\) 和实际值\(y\) 有多接近，

\[L(\widehat y,y) = \frac{1}{2}{(y - \widehat y)^2} \]

但是上面这种损失函数的缺点是最低点的极值不止一个，可能在使用梯度下降接近寻找损失函数最低点时会遇到困难，所以不使用上面这种损失函数，而采用下面这种：

\[L(\widehat y,y) = - \left[ {y*\log ( \widehat y) + (1 - y)*\log (1 - \widehat y)} \right] \]

当实际结果\(y=0\) 时，

\[L(\widehat y,y) = -\log (1 - \widehat y) \]

此时要想损失函数小，即\(-\log (1 - \widehat y)\) 小，即\(\log (1 - \widehat y)\) 大，则需要\(\widehat y\) 尽可能小，但是\(\widehat y\) 介于\(0 \sim 1\) 之间，所以此时\(\widehat y=0\) ，和实际情况\(y=0\) 接近。

当实际结果\(y=\) 1时，

\[L(\widehat y,y) = -y\log (\widehat y) \]

此时要想损失函数小，即\(-\log (\widehat y)\) 小，即\(\log (\widehat y)\) 大，则需要\(\widehat y\) 尽可能大，但是\(\widehat y\) 介于\(0 \sim 1\) 之间，所以此时\(\widehat y=\) 1，和实际情况\(y=1\) 接近。

损失函数（Loss function）是在单个训练样本中定义的，衡量的是单个训练样本上的表现，要想衡量在多个训练样本乃至训练集上的表现，要看成本函数（Cost function）

成本函数（Cost function）：衡量的是在全体的训练样本上表现

成本函数（Cost function）：

\[J(w,b) = \frac{1}{m}\sum\limits_{i = 1}^m {L({{\widehat y}^{(i)}},{y^{(i)}})} = - \frac{1}{m}\sum\limits_{i = 1}^m {\left[ {{y^{(i)}}*\log ({{\widehat y}^{(i)}}) + (1 - {y^{(i)}})*\log (1 - {{\widehat y}^{(i)}})} \right]} \]

其中\(\widehat y^{(i)}\) 是用一组特定的参数\(w\) 和 \(b\) 通过logistic回归算法得出的预测输出值