量子搜索算法 Grover search
问题定义:
Problem:
\(f: \{ 0,1,2,3,……,N-1 \} \rightarrow \{0,1\}\)
找到 \(f(x)=1\) 的x
解法
经典解法:
经典解法很简单,就是把每一个都看一遍,如果只有一个x对应的f(x)=1,那么平均是要看一半,才能找到那个x。
时间复杂度O(N)
量子解法:
使用Grover search 算法,时间复杂度在 \(O(\sqrt N)\)
Grover search 算法
Grover search 算法一共分为两步:
- Phase Inversion
- Inversion about the Mean
然后不断的迭代这两步我们就能够得到结果了。
首先我们先看看这两个步骤分别在做什么:
我们把 $f(x)=1 $ 的 \(|x\rangle\) 称为 \(x^*\) ,我们要找的也就是这个 \(x^*\) 。
Phase Inversion:
这一步主要是把 \(x^*\) 的概率幅翻转,变成负数,而其他的保持不变。
即,把 \(\sum_{x } \alpha_x|x\rangle\) 变成 \(\sum_{x \neq x^*} \alpha_x|x\rangle -\alpha_{x^*}|x^*\rangle\)
Inversion about the Mean
这一步呢,就是把 \(\alpha_x\) 变成 \(2\mu- \alpha_x\)
\(\mu\) 是所有概率幅的平均值,\(\mu= \frac{\sum_x \alpha_x}{N}\)
用图可能更好表达这两个步骤究竟在做什么:
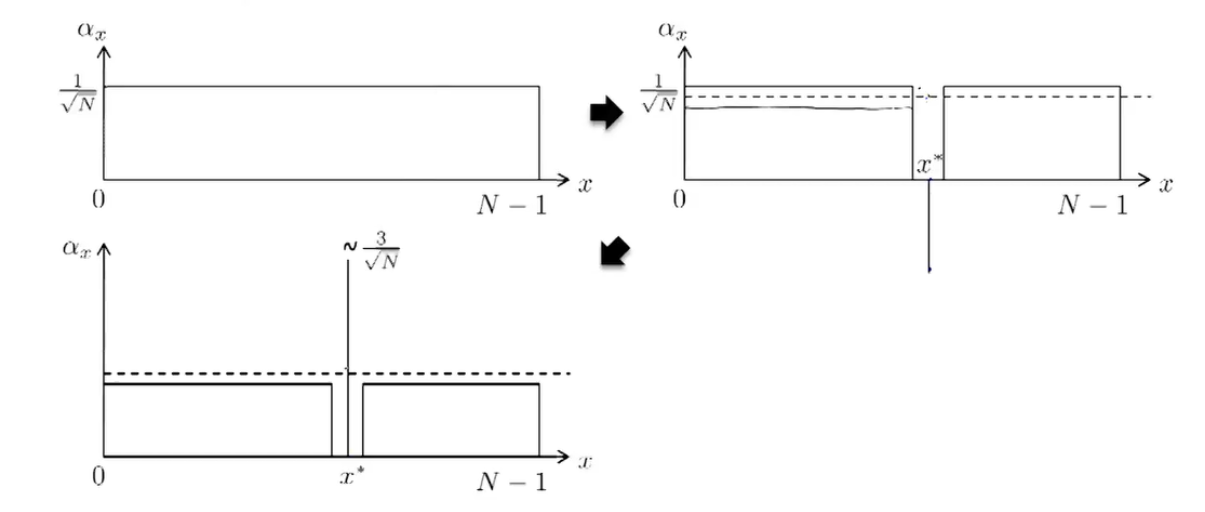
图1到图2,就是Phase Inversion,把\(x^*\)的概率幅翻转到了下面,图2中的虚线就是我的概率幅的平均值,图2到图3 就是我们的Inversion about the Mean,对着平均值翻转一次,其余x的概率幅是高于平均值的,所以 \(2\mu- \alpha_x\) 让他们变小了,而我们的 \(x^*\) 他的概率幅是个负数,所以 \(2\mu- \alpha_x\) 后他增加了。
不断的重复这个步骤, \(x^*\) 他的概率幅会越来越大,最后我们测量的时候就会很容的找到他。
进行了 \(\sqrt N\) 后,他的概率幅就会达到 \(\frac{1}{ \sqrt 2}\) ,算概率就是1/2。
那么接下来的问题就是,这些操作是怎么实现的?
Phase Inversion:
这个步骤要做的事情就是,
把 \(\sum_{x } \alpha_x|x\rangle\) 变成 \(\sum_{x \neq x^*} \alpha_x|x\rangle -\alpha_{x^*}|x^*\rangle\)
符号是和f(x)是否为1相关的,进一步化简就是 \(\sum_x (-1)^{f(x)} \alpha_x|x\rangle\)
有没有一丝熟悉感?
把f(x)的结果给放到相位上去,这是我们在Parity Problem中就遇到的问题。
当时的解决方法是把答案比特变成 \(|-\rangle\)。
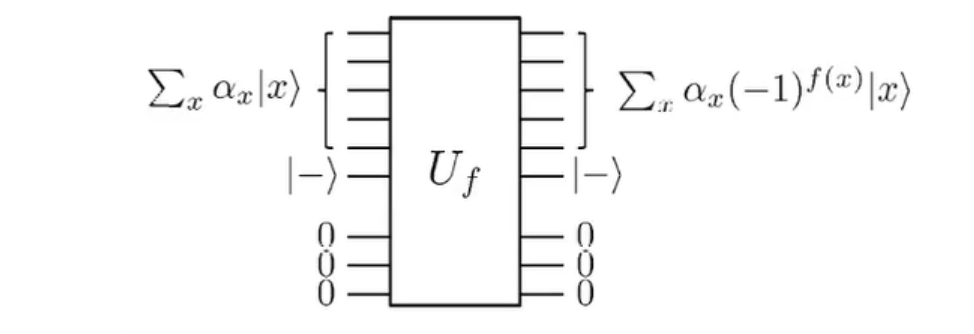
一般情况,如果我们打算放置答案的比特是 \(|b\rangle\),那么输入的比特就是\(|b \oplus f(x)\rangle\)
如果f(x)=0 那么\(|( \frac{1}{\sqrt2}|0\rangle-\frac{1}{\sqrt2}|1\rangle) \oplus f(x) \rangle = \frac{1}{\sqrt2}|0\rangle-\frac{1}{\sqrt2}|1\rangle = |-\rangle\)
如果f(x)=1 那么\(( \frac{1}{\sqrt2}|0\rangle-\frac{1}{\sqrt2}|1\rangle) \oplus f(x) \rangle = \frac{1}{\sqrt2}|1\rangle-\frac{1}{\sqrt2}|0\rangle = -|-\rangle\)
最后一个比特的值如果在\(|+\rangle |-\rangle\)坐标下测量,一定是 \(|-\rangle\),f(x)的差别也变到了符号上,即 \((-1)^{f(x)}\)
Inversion about the Mean
把 \(\alpha_x\) 变成 \(2\mu- \alpha_x\) ,这个就要比前一个麻烦了
这其实是要求我把现在的态对着 \(\mu\) 翻转。
对着 \(\mu\) 翻转会吗?
不太会。
但是我会对着 \(|0\rangle\) 的翻转啊。
对角线第一个值为1,其余为-1,非对角线的都为0。
\(\left[ \begin{array}{} 1 & 0 & …& 0 \\ 0 & -1 & …& 0 \\…\\0 & 0 & …& -1 \end{array}\right]\left[ \begin{array}{} a_0\\a_1\\…\\a_{n-1} \end{array}\right]=\left[ \begin{array}{} a_0\\-a_1\\…\\-a_{n-1} \end{array}\right]\)
这个矩阵轻而易举的可以让 \(|0\rangle\) 保持不变,非 \(|0\rangle\) 的符号全都翻转。
量子变换要求矩阵式酉矩阵,这个矩阵很明显满足 \(UU^\dagger=U^\dagger U=I\)
接下来怎么做呢?
我们先把我们的态整体来一个从 \(|\mu\rangle\) 到 \(|0\rangle\) 的旋转,对着 \(|0\rangle\) 翻转后,又从 \(|0\rangle\) 到 \(|\mu\rangle\) 翻转回去。
\(|\mu\rangle\) 是一个怎样的态?
所有的x的概率都一样,也就是我们的superposition \(\frac{1}{2^{\frac{n}{2}}} \sum_{x \in \{0,1 \}^n}|x\rangle\)
\(\frac{1}{2^{\frac{n}{2}}} \sum_{x \in \{0,1 \}^n}|x\rangle\) 和 \(|0\rangle\)之间的相互转换,这就是我们最最熟悉的Hadamard Transform了
第二部分的电路图如下:
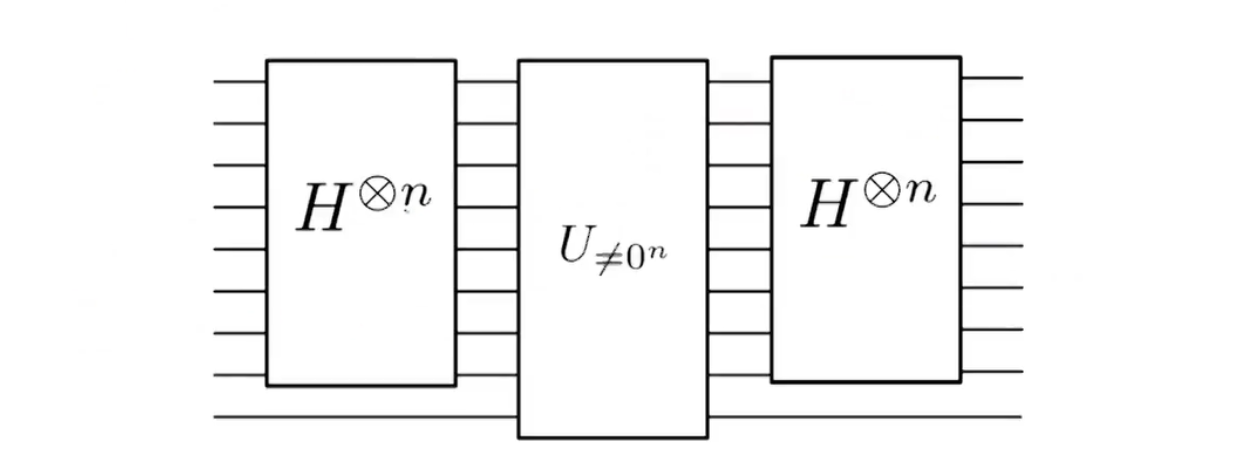
这个矩阵是可以直接计算的:

我这里直接给出答案,得到的矩阵值呢是下图左边的这个矩阵:
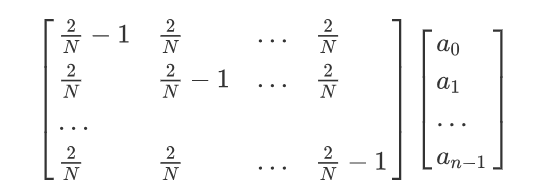
在对应的 \(\alpha_x\)的结果恰好是 \(\frac{2}{N} \sum _{y=0}^{N} \alpha_y -\alpha_x\)
而 \(\frac{2}{N} \sum _{y=0}^{N} \alpha_y\) 恰好就是 \(2\mu\)
至此,呈上最完整的电路图模块:
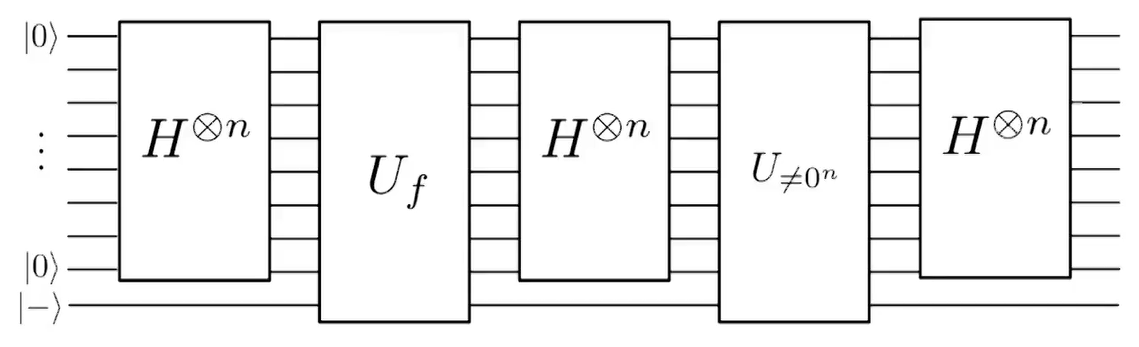
第一个H门是数据的初始化,第二个门是为了翻转 \(x^*\),第三四五个门是为了对 \(| \mu \rangle\) 翻转,二三四五这四个门就是要给重复的模块了,不断的重复他们就可以不断的提高 \(x^*\)的概率幅,最终找到 \(x^*\)。
参考资料:




