简单的量子算法(二):Simon's Algorithm
前情回顾:
简单的量子算法(一):Hadamard 变换、Parity Problem
好的,现在开始正版的故事,Simon’s Algorithm
问题:
有一个secret string,是n位的0,1串 \(s \in \{0,1 \} ^n\)
现在有一个黑盒子,f(x),我们对他唯一的了解就是 \(f(x)=f(x \oplus s)\) ,输入的x也是n位的0,1串 \(x \in \{0,1 \} ^n\)
请问,要多少次,我们可以找到这个secret string?
经典解法:
如果我们能找到 \(x\) 和 \(x \oplus s\) ,那么非常容易,就可以得到s,只要 \(x\oplus x\oplus s\) 。
那么如果找到两个输入拥有相同的输出呢?
这个问题其实是另一个大家都很熟悉的问题的变形,一群人中,要多少人就有两个人的生日是相同的,印象中,23人两个人的生日是相同的概率就大于50%了,如果有60个人,那么两个人生日相同的概率就超过99%了。
这个问题和生日问题的解法是一样的,就不再累述了,想要知道的请搜索生日问题,在这里,我们给出一个大概的答案,是 \(2^{n/2}\) c次。
量子解法:
量子解法一共有三步:
- set up random superposition $ \frac{1}{\sqrt2} |r\rangle +\frac{1}{\sqrt2} |r \oplus s \rangle$
- Fourier Sample to get a random y: \(y·s=0 (\mod 2)\)
- repeat step n-1 times to generate n-1 linear equation.
接下来,我们来一步一步的看每个步骤在做什么,以及怎么做:
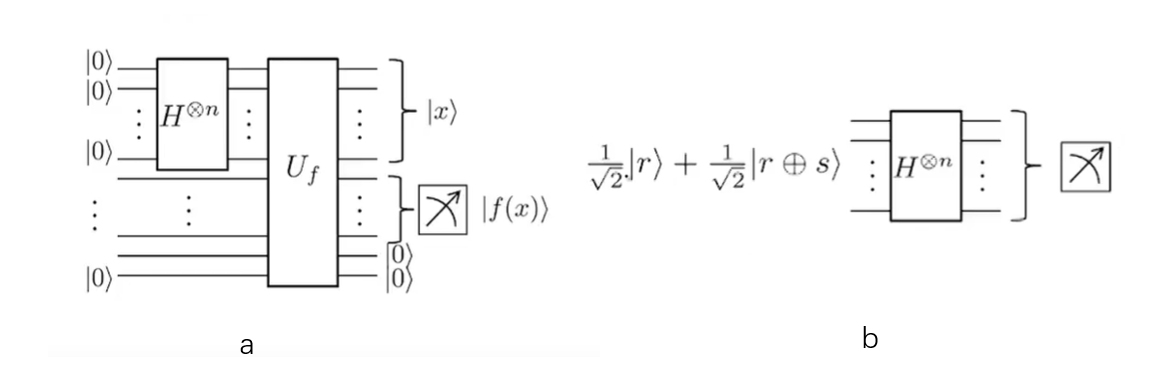
第一步,制造叠加态 $ \frac{1}{\sqrt2} |r\rangle +\frac{1}{\sqrt2} |r \oplus s \rangle$ ,这个可以通过图a实现。
首先通过第一个\(H ^{\otimes n}\) 门,我们n比特的 \(|0\rangle\) 就成功的变成了叠加态 $\frac{1}{2^{\frac{n}{2}}} \sum_x |x\rangle $
和 \(|b\rangle\) 一起通过 \(U_f\) ,得到的结果是 $\frac{1}{2^{\frac{n}{2}}} \sum_x |x\rangle|b\oplus f(x) \rangle $
测量 \(|b\oplus f(x) \rangle\) ,只有结果是测量结果的 \(|x\rangle\)还在,其他的 \(|x\rangle\) 都会坍缩,基于这个黑盒子的特性,那么只有 $|r\rangle $ 和 \(|r \oplus s \rangle\) 会留下来,因为他们的f(x)是一样的,r是任意的一个序列,测量的结果对应哪个r就是哪个r。
至此我们得到了想要的叠加态 $ \frac{1}{\sqrt2} |r\rangle +\frac{1}{\sqrt2} |r \oplus s \rangle$
第二步,Fourier Sampling
对我们得到的叠加态 $ \frac{1}{\sqrt2} |r\rangle +\frac{1}{\sqrt2} |r \oplus s \rangle$ Fourier Sampling
再次通过\(H ^{\otimes n}\) 我们能得到什么?
依照我们在简单的量子算法(一)中的结论,我们知道 \(H^{\otimes n} |u\rangle = \sum_x \frac{-1^{u·x}}{2^{\frac{n}{2}}} |x\rangle\) 。
那么
此时,我们的问题已经集中在了 \(1^{r·x}+(-1)^{(r\oplus s)·x}\) 上。
\((-1)^{(r\oplus s)·x}\) 可以写成\((-1)^{s·x}*(-1)^{r·x}\) (至于为什么可以,大家可以试一下都是按位操作,一共也就4种可能
那么每种可能的概率的公式就可以写成\(\frac{((-1)^{s·x}+1)*(-1)^{r·x}}{2^{(n+1/2)}}\)
如果 \(s·x=0\) 那么,这个概率正好为 \(\frac{(-1)^{r·z}}{2^{(n-1)/2}}\)
如果 \(s·x=-1\) 那么,这个概率正好为0
那么这又说明了什么呢?
这个说明只要我们测量 \(|x\rangle\) ,那么我们得到的x一定是 \(s·x=0\) 的,因为不为0的都被抵消了。
那么得到了x,又意味着什么呢?
\(s·x=0\) 事实上我们是得到了一个等式 $s_1x_1+s_2x_2+……+s_nx_n =0 \mod 2 $
第三步:
如果我们把第一次测量得到的x编号为 \(x^1\) ,那么我们得到了等式 $s_1x_11+s_2x_21+……+s_nx_n^1 =0 \mod 2 $
第二次测量,得到等式 $s_1x_11+s_2x_21+……+s_nx_n^1 =0 \mod 2 $
以此类推,测量n-1次,得到了n-1个等式的方程式组。
$s_1x_11+s_2x_21+……+s_nx_n^1 =0 \mod 2 $
$s_1x_11+s_2x_21+……+s_nx_n^1 =0 \mod 2 $
……
$s_1x_1{n-1}+s_2x_2+……+s_nx_n^{n-1} =0 \mod 2 $
n-1个等式,n个未知数( \(s_1,s_2,……,s_n\) ),一般来说会有两组解,一组是全零的平凡解,这个是我们不要的,而另一组解就是我们的答案 \(s\) 。
成功的概率:
上述的解方程有一个前提,那就是这是一个线性方程组,如果这个不是线性的,那么测量n-1次是不可能得答案的。
那么我测量得到的x组成的方程是线性方程的概率是多少呢?
我们可以列一个表格来看看:
| 失败的情况 | 失败的概率 | 成功的概率 | |
|---|---|---|---|
| \(x^1\) | 0 | \(\frac{1}{2^{n-1}}\) | \(1-\frac{1}{2^{n-1}}\) |
| \(x^2\) | 0、 \(x^1\) | \(\frac{2}{2^{n-1}}\) | \(1-\frac{1}{2^{n-2}}\) |
| \(x^3\) | 0 、 \(x^1\) 、\(x^2\) 、\(x^1+x^2\) | \(\frac{4}{2^{n-1}}\) | \(1-\frac{1}{2^{n-3}}\) |
| …… | …… | ………… | \(1-\frac{1}{2^{n-1}}\) |
| \(x^{n-1}\) | 0 、 \(x^1\) ……\(x^1+x^2\)……\(x^1+x^2+……+x^n-2\) | \(\frac{2^{n-2}}{2^{n-1}}\) | \(1-\frac{1}{2}\) |
每次的测量失败的情况分为以下三种情况:
- 测量出来全是0
- 测量出来结果和前面的是一样的
- 测量出来的结果是前面测量结果的线性组合
因为这里算的成功概率都是独立的成功概率,所以要算整体的成功概率是他们的乘积
\(\frac{1}{2}*\frac{3}{4}*\frac{7}{8}*……*\frac{2^{n-1}-1}{2^{n-1}}\)
上面这个式子求极限是一个q series的问题,感兴趣的朋友可以去查一下怎么求解,这里直接给出概率,约等于0.28878
注意:
大家是不是以为这样子就万事大吉了?
No,这里还有一个需要注意的地方,可能很多朋友已经意识到了,量子态不是测量完就坍塌吗?为什么可以测量n-1次?
事实上,这是把第一部分给做了n-1次,这样你才可以有n-1个 \(|x\rangle\) 给你测量找出满足线性条件的x。
参考资料:




