简单的量子算法(一):Hadamard 变换、Parity Problem
Hadamard Transform
Hadamard 变换在量子逻辑门中提过,只不过那时是单量子的Hadamard门,负责把\(|1\rangle\)变成\(|-\rangle\),\(|0\rangle\)变成\(|+\rangle\)。
那么对多量子的Hadamard门呢?
对于多量子逻辑门,其实说过一句,是单量子逻辑门的张量积。
对于多量子比特的Hadamard门,就是把每一个量子比特都由\(|1\rangle\)变成\(|-\rangle\),\(|0\rangle\)变成\(|+\rangle\),或者\(|-\rangle\)变成\(|1\rangle\),\(|+\rangle\)变成$|0\rangle $ 。如果是n个比特,那么这n比特的Hadamard门就可以写作是 \(H^{\otimes n}\) ,矩阵表达就是 \(H^{\otimes n}=\left[ \begin{array}{}{\frac{1}{\sqrt2}} &{\frac{1}{\sqrt2}} \\ {\frac{1}{\sqrt2}}&{-\frac{1}{\sqrt2}} \end{array}\right] \otimes ……\otimes \left[ \begin{array}{}{\frac{1}{\sqrt2}} &{\frac{1}{\sqrt2}} \\ {\frac{1}{\sqrt2}}&{-\frac{1}{\sqrt2}} \end{array}\right]\) (张量积n次)
对于\(|0\rangle\),变成\(\frac{1}{\sqrt2}|0\rangle+\frac{1}{\sqrt2}|1\rangle\)。
对于\(|00\rangle\),变成\((\frac{1}{\sqrt2}|0\rangle+\frac{1}{\sqrt2}|1\rangle)(\frac{1}{\sqrt2}|0\rangle+\frac{1}{\sqrt2}|1\rangle)\) ,即 \(\frac{1}{2}|00\rangle+\frac{1}{2}|01\rangle+\frac{1}{2}|10\rangle+\frac{1}{2}|11\rangle\) 可能性均等的所有可能 的叠加。
那么对于n个 \(|0\rangle\) 呢?则是变成了 \(\frac{1}{2^{\frac{n}{2}}} \sum_{x \in \{0,1 \}^n}|x\rangle\) ,x是由0、1组成的所有的长度为n的数字串。
那么更进一步,如果我的n比特不是 \(|0\rangle\),而是 \(|0\rangle\) 、 \(|1\rangle\) 随意切换呢?比如数字串 \(|u\rangle=|u_1u_2……u_n\rangle\) ,如果输入是 \(|u\rangle\) ,那么经过H门变换,输出会是什么?
输出是:\(\sum_x \frac{-1^{u·x}}{2^{\frac{n}{2}}} |x\rangle\) ,这里 \(u·x=u_1x_1+u_2x_2+……+u_nx_n\)
原因如下:
对于\(|0\rangle\),H门变成\(\frac{1}{\sqrt2}|0\rangle+\frac{1}{\sqrt2}|1\rangle\)
对于\(|1\rangle\),H门变成\(\frac{1}{\sqrt2}|0\rangle-\frac{1}{\sqrt2}|1\rangle\)
如果想要有一个负号,则需要这一位在输入的时候是\(|1\rangle\) ,并且输出的时候也是 \(|1\rangle\) ,同时,如果在这个数字串中这种情况出现了偶数次(即有偶数位的比特在输入输出的时候都是\(|1\rangle\)),那么整体情况就会是负负得正,所以我们将每位的情况相乘,再连加(对于不会造成负号的情况,他们相乘的结果是0),作为-1的指数来标明符号。
而以上的变换,在量子计算中又称为Fourier Sampling。
整理一下本小节的内容: \(H^{\otimes n} |u\rangle = \sum_x \frac{-1^{u·x}}{2^{\frac{n}{2}}} |x\rangle\) ,他将我们的输入数据给移到了符号上面去。
Parity Problem
这个问题是hadamard变换的简单应用。
假设: 有这么一个黑盒子 把长度为n的0、1数字串映射成0或者1一个数字 \(f: \{ 0,1 \}^n \rightarrow \{0,1 \}\) ,已知映射的规则如下 \(f(x)=u·x=u_1x_1+u_2x_2+……+u_nx_n \mod 2\) 模2的意思是如果是累加的和是奇数,那么就是1,偶数就是0
问题:请问,我至少需要试几次,才能知道u是什么?
经典解法:
输入100……0 得到\(u_1\) 的值
输入010……0 得到\(u_2\) 的值
输入001……0 得到\(u_3\) 的值
……
输入000……1 得到\(u_n\) 的值
因为我们的输出结果只有一位的信息,而u的全部信息有n位,所以我们至少也需要n次。
量子解法:
这个量子解法又叫做 Bernstein-Vazirani算法,一共只有两步:
一、制造出一个量子叠加态 : $\frac{1}{2^{n/2}}\sum_x (-1)^{f(x)} |x\rangle $
二、对这个叠加态fourier sampling
why?
对于第一步我们需要制备出来的量子叠加态,不知道大家有没有眼熟,这个是我们上一节的结论,将\(|u\rangle\) 作为H门的输出得到的结果一模一样。
我们已经知道了量子计算是可逆的,对于H门来说,连续两个的H门操作就是完全抵消的,第一个H门将\(|0\rangle\)变成\(|+\rangle\),第二个H门又将\(|+\rangle\)变成\(|0\rangle\)。
所以,我们能够将$\frac{1}{2^{n/2}}\sum_x (-1)^{f(x)} |x\rangle $用H门变换出来,把f(x)的值移到符号上,那么我们也可以通过H门把符号上的f(x)移到输出里,只需要一个同样的H门操作,也就是我们的第二步。
所以现在的问题变成了,如果制备叠加态 $\frac{1}{2^{n/2}}\sum_x (-1)^{f(x)} |x\rangle $ 呢?
在量子电路里面我们已经讨论过了,一个量子的电路,为了让他可逆,我们一般是输入 \(|x\rangle|b\rangle\) 然后输出是 \(|x\rangle |b \oplus f(x) \rangle\) 把输入的结果f(x)模2加到b上。
因为是需要所有的x,所以首先用H门,将n比特的 \(|0\rangle\) 变成所有状态均可能的叠加态 \(\frac{1}{2^{\frac{n}{2}}} \sum_{x \in \{0,1 \}^n}|x\rangle\) 。
接下来,把 \(|-\rangle =\frac{1}{\sqrt2}|0\rangle-\frac{1}{\sqrt2}|1\rangle\) 作为 \(|b\rangle\) 和前面的叠加态 \(\frac{1}{2^{\frac{n}{2}}} \sum_{x \in \{0,1 \}^n}|x\rangle\) 一起输入 \(U_f\) 。
此时输入是 \(\frac{1}{2^{\frac{n}{2}}} \sum_x |x\rangle |-\rangle\)
输出是 \(\frac{1}{2^{\frac{n}{2}}} \sum_x |x\rangle |- \oplus f(x) \rangle\)
如果f(x)=0 那么\(|- \oplus f(x) \rangle = \frac{1}{\sqrt2}|0\rangle-\frac{1}{\sqrt2}|1\rangle = |-\rangle\)
如果f(x)=1 那么\(|- \oplus f(x) \rangle = \frac{1}{\sqrt2}|1\rangle-\frac{1}{\sqrt2}|0\rangle = -|-\rangle\)
最后一个比特的值如果在\(|+\rangle |-\rangle\)坐标下测量,一定是 \(|-\rangle\),f(x)的差别也变到了符号上,即 \((-1)^{f(x)}\)
此时,我们的输出已经是 \(\frac{1}{2^{n/2}}\sum_x (-1)^{f(x)} |x\rangle |-\rangle\) ,只看前面的部分,就是我们需要的叠加态了。
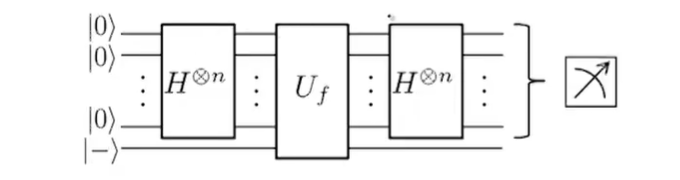
概括一下,概括一下,通过H门制备出一个均等可能的态,然后和 \(|-\rangle\) 一起通过 \(U_f\) 将f(x)的结果移到符号上,最后再次通过H门,把符号上的结果移下来,整个电路图如下图所示,非常的简单,在经典算法需要多项式时间的时候,量子算法只需要常数的时间。
下一篇的内容是simon's Algorithm是在parity Problem的又一个进化,也是基于H门的,所以说H门很重要啊,基本上所有的量子算法不管要干嘛,先来一个H门再说,毕竟这个是用n比特同时表达 \(2^n\) 个数据的法宝。




