量子逻辑门
量子态的演化
在前面量子纠缠1中我们已经提到了量子比特的线性代数表示,即,对于一个量子态 \(\alpha_0 | 0\rangle +\alpha_1 | 1\rangle\)我们可以化简成$ \left[ \begin{array}{}{\alpha_0} \ {\alpha_1}\end{array}\right]$ 。
量子态不是一成不变的,就像高电平会变成低电平,一个量子态也能演化成另一个量子态,量子态的演化就是在Hilbert空间中的旋转,如图(a)所示。
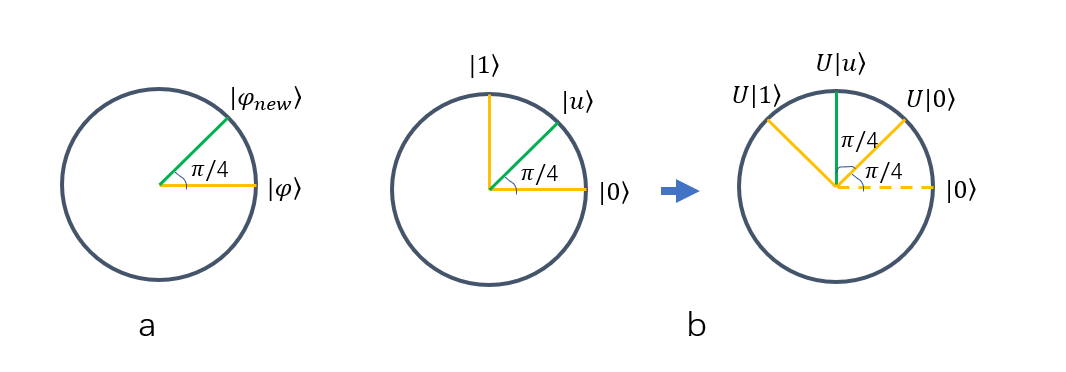
通过一个U操作,我们就将 \(| 0\rangle\) 变成了 \(U| 0\rangle\) , \(| 1\rangle\) 变成了 \(U| 1\rangle\) , \(| u\rangle\) 变成了 \(U| u\rangle\) ,如图(b)所示。需要注意的是,我添加一个U操作,没有改变 \(| 0\rangle\) 、 \(| 1\rangle\) 、 \(| u\rangle\) 之间的关系, \(U| 0\rangle\) 、 \(U| 1\rangle\) 和 \(| 0\rangle\) 、 \(| 1\rangle\) 一样,他们之间的关系依旧是垂直。
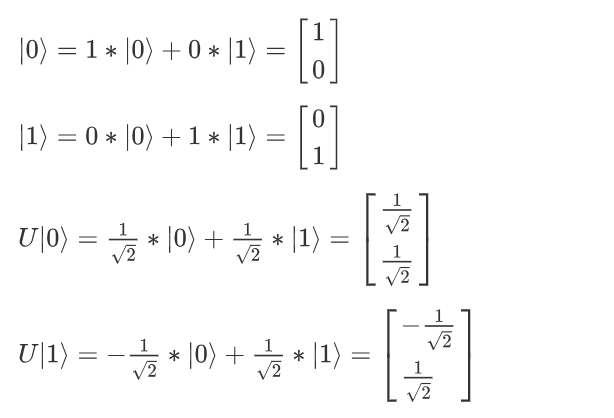
$ (| 0\rangle, | 1\rangle)=0$
$ (U| 0\rangle, U| 1\rangle)=0$
\((,)\) 是内积的意思, $ (| 0\rangle, | 1\rangle)= \left[ \begin{array}{}{1}&{0}\end{array}\right]\left[ \begin{array}{}{0} \ {1}\end{array}\right]$ ,同样,也可以简写成 \(\langle0| 1\rangle\) , \(\langle0|\) 表明是 \(| 0\rangle\) 的共轭转置。
对于这种两个向量之间夹角不会变的旋转称为刚性旋转 rigid rotation。
而这种U操作被成为酉操作,也是unitary transformation
Unitary Transformation
量子比特我们用向量来表示,因为我们量子比特的演化是线性的,所以在量子比特上的操作,可以用矩阵来表示。
单量子比特是 \(2*1\) 的向量,则单量子比特门是 \(2*2\) 的矩阵。
\(| 0\rangle\) 变到 \(U| 0\rangle\) 在线性代数上就是 $ \left[ \begin{array}{}{1} \ {0}\end{array}\right]$ 变到 $ \left[ \begin{array}{}{\frac{1}{\sqrt2}} \ {\frac{1}{\sqrt2}}\end{array}\right]$
对于旋转了 \(\theta\) 角度的操作,都可以用 \(U_{\theta}= \left[ \begin{array}{}{cos\theta} &{-sin\theta} \\ {sin\theta}&{cos\theta} \end{array}\right]\) 表达。
如果要做相反操作,就是将顺时针转 \(\theta\) 角度, \(U_{-\theta}= \left[ \begin{array}{}{cos\theta} &{sin\theta} \\ {-sin\theta}&{cos\theta} \end{array}\right]\)
很巧的是, \(U_\theta^\dagger=U_{-\theta}\) , \(\dagger\) 是共轭转置的意思。
\(U_\theta U_{\theta}^\dagger=I\) ,意思也很好理解,因为顺时针 \(\theta\) 又 \(-\theta\) ,正好就回到原位。
事实上所有的量子操作都是可逆的,所有的量子操作都酉操作。
那么什么是酉操作呢?
U is unitary iff \(U^\dagger U =I\)
对于酉矩阵的更多特征会在线性代数的章节提到,这里主要提一个,酉矩阵是保内积的。
保内积又是什么意思?
两个向量在乘以相同的U后,他们的内积不变。
单量子逻辑门
量子逻辑门和经典逻辑门一个巨大的不同是——量子逻辑门可逆。
经过了经典的逻辑门与门或者非门,我们的信息会丢失,告诉你与门后的输出结果是0,你知道与门前的输入吗?(0,0)、(0,1)、(1,0)都有可能。
而对于量子逻辑门来说,我经过U变换后的结果是 \(|a\rangle\) ,那么 \(U^\dagger |a\rangle\) 就是变换前的输入了。
举例几个常用的单量子逻辑门:
\(X=\left[ \begin{array}{}{0} &{1} \\ {1}&{0} \end{array}\right]\),X门又称为比特翻转,他可以把 \(|0\rangle\) 变成 \(|1\rangle\) ,把 \(|1\rangle\) 变成 \(|0\rangle\) 。
\(Y=\left[ \begin{array}{}{0} &{-i} \\ {i}&{0} \end{array}\right]\)
\(Z=\left[ \begin{array}{}{1} &{0} \\ {0}&{-1} \end{array}\right]\),Z门又称为相位翻转门,可以把 \(|+\rangle\) 变成 \(|-\rangle\) , \(-|1\rangle\) 变成 \(|1\rangle\) 。
以及一个特别有用的门,Hadamard门:
\(H=\left[ \begin{array}{}{\frac{1}{\sqrt2}} &{\frac{1}{\sqrt2}} \\ {\frac{1}{\sqrt2}}&{-\frac{1}{\sqrt2}} \end{array}\right]\) ,他的作用是把 \(|1\rangle\) 变成 \(|-\rangle\) , \(|0\rangle\) 变成 \(|+\rangle\) 。
两量子逻辑门
对于两量子比特来说,他们的状态是 \(\alpha_{00} | 00\rangle+\alpha_{01} | 01\rangle+\alpha_{10} | 10\rangle+\alpha_{11} | 11\rangle\) ,需要用 \(4*1\) 的向量来描述,也就是 $ \left[ \begin{array}{}{\alpha_{00}} \ {\alpha_{01}} \ {\alpha_{10}} \ {\alpha_{11}} \end{array} \right]$ ,对应操作两比特的逻辑门,也就是 \(4*4\) 的矩阵了。
两比特的量子门有各自管各自的,如图(c),也有一个控制另一个的,如图(d)。
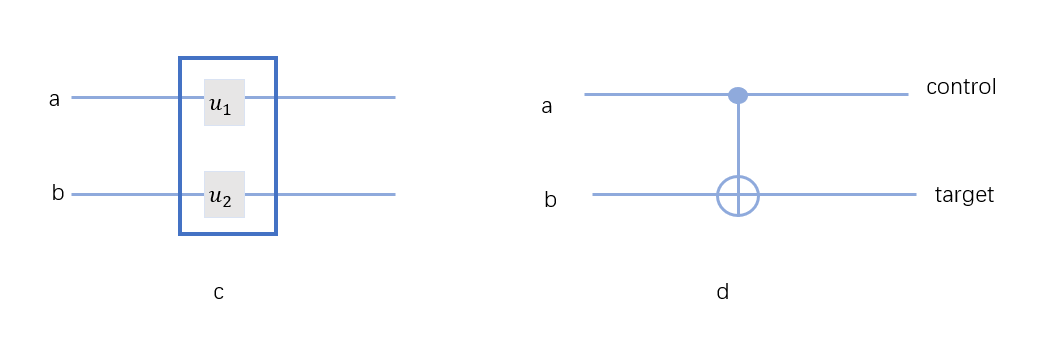
对于图c来说, \(U=u_1\otimes u_2\) ,如果 \(u_1=\left[ \begin{array}{}{a} &{c} \\ {b}&{d} \end{array}\right],u_2=\left[ \begin{array}{}{e} &{g} \\ {f}&{h} \end{array}\right]\) ,那么, \(U=\left[ \begin{array}{}{a\left[ \begin{array}{}{e} &{g} \\ {f}&{h} \end{array}\right]} &{c\left[ \begin{array}{}{e} &{g} \\ {f}&{h} \end{array}\right]} \\ {b\left[ \begin{array}{}{e} &{g} \\ {f}&{h} \end{array}\right]}&{d\left[ \begin{array}{}{e} &{g} \\ {f}&{h} \end{array}\right]} \end{array}\right]\) ,这也就是张量积的算法。
对于图d来说,这是一个受控非门CNOT门,他的意思是,如果a是0,那么b保持不变,如果a是1,那么b就是变成相反的,比如 \(|0\rangle\) 变成 \(|1\rangle\) ,或者把 \(|1\rangle\) 变成 \(|0\rangle\) 。
即 \(|00\rangle to|00\rangle,|01\rangle to|01\rangle,|10\rangle to|11\rangle,|11\rangle to|10\rangle\) 。
用矩阵来描述就是 \(\left[\begin{array}{cccc}{1} & {0} & {0} & {0} \\ {0} & {1} & {0} & {0} \\ {0} & {0} & {0} & {1} \\ {0} & {0} & {1} & {0}\end{array}\right]\) 。
至此,主要的量子逻辑门就介绍完毕,如果想要动手实践的话,有阿里的量子计算云平台、华为的hiQ、IMB的IBM Q
参考资料




