atcoder做题记录
AGC001
B Mysterious Light
射出两条射线后,问题变成了:有一个邻边长分别为 \(x,y\) ,夹角为 \(60°\) 的平行四边形,求从某个角射出光线后的总长度。显然可以递归求解。复杂度为 \(\mathcal O(\log n)\) 。
C Shorten Diameter
显然最后留下的是一个连通块。无根树转有根树,那么最终剩下的连通块的直径的一个端点一定是深度最深的那个点 \(u\) 。枚举 \(u\) ,那么所有深度不大于 \(u\) 且距离 \(u\) 不超过 \(k\) 的点都是可行的。暴力找出这些点即可。复杂度为 \(\mathcal O(n^2)\) 。
D Arrays and Palindrome
构造题一生之敌了属于是。
关键思想是如下图的构造方式,即错开一位。
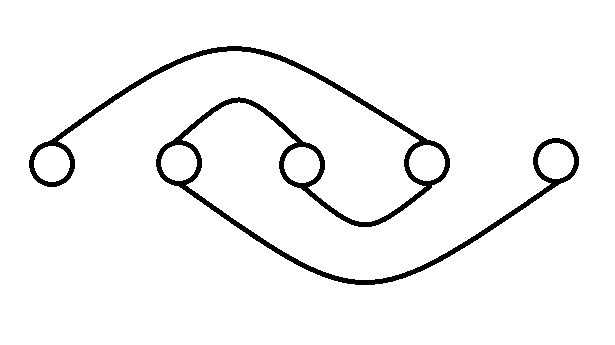
实现时还有一些细节需要注意。复杂度为 \(\mathcal O(m)\) 。(然而 \(m\le 100\) 。。。)
E BBQ Hard
考虑柿子 \(\dbinom {a_i+b_i+a_j+b_j}{a_i+a_j}\) 的组合意义是从 \((0,0)\) 出发走到 \((a_i+a_j,b_i+b_j)\) 的方案数。为了使变量 \(i,j\) 分离,可以看作是从 \((-a_i,-b_i)\) 出发走到 \((a_j,b_j)\) 的方案数。于是原问题等价于有若干起点 \((-a_1,-b_1)\sim(-a_n,-b_n)\) ,有若干终点 \((a_1,b_1)\sim(a_n,b_n)\) ,求总方案数。做一个简单dp即可。
复杂度为 \(\mathcal O(n+\max a\cdot\max b)\) 。
F Wide Swap
原操作不知道该如何刻画了,因此考虑在排列的逆上对应的操作:即如果相邻的两个元素之差不小于 \(k\) 则可以交换。最终目标仍然是最小化字典序。
我们可以联想到经典的冒泡排序,但是复杂度为 \(\mathcal O(n^2)\) ,过不了。考察其他复杂度较低的算法后发现可以套用归并排序,即先分治两边处理 (假设区间为 \([l,r]\) ,分治中点为 \(mid\) ) ,合并时区间 \([mid+1,r]\) 的数 \(u\) 先归并当且仅当 \(u+k\) 不大于此时区间 \([l,mid]\) 剩下的数的最小值,对应到初始情况就是某个后缀最小值。于是预处理后缀最小值即可。
复杂度为 \(\mathcal O(n\log n)\) 。
AGC002
B Box and Ball
直接模拟出所有情况显然是不可能的。不过我们可以计算出红球在每个盒子里的概率,从而得到答案。直接浮点数计算会有精度问题,可以通过对某个大质数取模解决。
复杂度为 \(\mathcal O(n+m)\) 。
C Knot Puzzle
考虑possible的必要条件是存在某个相邻的两根绳子长度之和不小于 \(L\) ,因为必然存在某时刻仅剩下两根相邻绳子。然后发现这也是充分的:保证这两条绳子间的绳结最后解开,其他的依次从外到内解即可。
复杂度 \(\mathcal O(n)\) 。
D Stamp Rally
整体二分或kruskal重构树。复杂度为 \(\mathcal O((n+q)\log m)\) 。
E Candy Piles
博弈论也是一生之敌我的评价是。
第一步非常巧妙的转化:将 \(a\) 降序排序后得到下图:(以 \(\{a\}=\{7,7,7,6,4,4,4,2,2\}\) 为例)

那么操作对应于要么删除最左侧的一列,要么删除最靠下的一行。非常具有对称性。
第二步非常巧妙的转化:游戏过程可以看作两人轮流操作,每次可以选择向上走/向右走,走到边界者输。如下图:
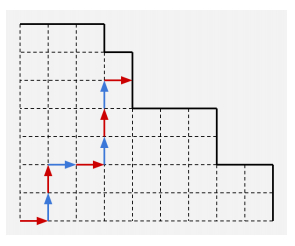
我们称某个点是必胜点当且仅当从此点出发先手必胜。类似定义必败点。那么显然网格边界都是必胜点,据此可推出所有点的情况。原点的情况就是答案。可见下图:
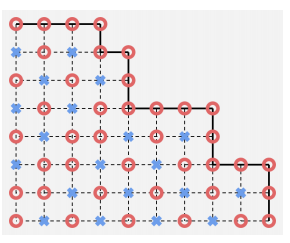
直接模拟复杂度过高。考察有性质:\((u,v)\) 的情况一定和 \((u+1,v+1)\) 的情况相同(证明可考虑反证法)。于是我们找到最大的 \(x\) 满足 \((x,x)\) 不在边界上。此点状态必然和原点相同。从 \((x,x)\) 出发,只能一直向上走或一直向右走,因此通过奇偶性就能得到该点的胜败状态。
复杂度为 \(\mathcal O(n)\) 。
F Leftmost Ball
问题可转化为有 \(n\) 个白球和 \(n\) 种其他颜色的球各 \(k-1\) 个,求合法排列方式的方案数。一个排列合法当且仅当对于任意前缀,白球个数不小于其他颜色种类数。
据此可设计dp状态:令 \(f_{i,j}\) 表示已经放了 \(i\) 个白球和 \(j\) 种其他颜色(每种颜色的 \(k-1\) 个全部都放了)后的方案数 \((j\le i)\) 。转移时考虑最靠前的未被放置球的位置,考察其是放白球还是放其他颜色的即可。方程为:
注意要特判 \(k=1\) 的情况。
复杂度为 \(\mathcal O(nk)\) 。
AGC003
C BBuBBBlesort!
通过无限使用操作2事实上可以对下标奇偶性相同位置排序。于是我们只需要将现在的下标和排序后下标奇偶性不同的位置用操作1处理掉即可。复杂度为 \(\mathcal O(n)\) 。
D Anticube
考虑对所有数质因数分解,然后将所有指数对3取模。之后对于 \(n=\prod_{i}p_i^{c_i}\) ,我们令 \(f(n)=\prod_ip_i^{3-c_i}\) 。将 \((n,f(n))\) 看作一对,对于每一对,我们将 \(\max(ct_n,ct_{f(n)})\) (其中 \(ct_n\) 表示 \(n\) 的出现次数),贡献到答案中即可。复杂度为 \(\mathcal O(n\sqrt V)\) ,无法通过。
不过事实上我们不需要质因数分解。“将所有指数对3取模”等价于除以一个尽可能大的完全立方数。现在的难点在于无法快速求 \(f(n)\) 。不过我们可以先分解出 \(n\) 的所有不大于 \(V^{\frac 13}\) 的质因数,此后剩下的数必然可分解为 \(p,p^2,pq\) 三种形式之一。而 \(f(p)=p^2,f(p^2)=p,f(pq)=p^2q^2\) ,因此只需要判断其是否是 \(p^2\) 的形式就行了。
复杂度为 \(\mathcal O(nV^{\frac 13})\) 。
E Sequential operations on Sequence
最终形成的序列可以用如下形式自顶向下描述:对于 \(i=1\sim k\) 序列 \(A_i\) 由序列 \(A_{i-1}\) 重复 \(a_{i-1}\) 次,而最后一次仅保留前 \(b_{i-1}\) 形成。特别地序列 \(A_0\) 是 \(1,2,3,\cdots,n\) 。
我们维护序列 \(f_i\) 表示 \(0\sim i\) 这些位置的数都出现了 \(f_i\) 次。当序列从 \(A_i\) 变为 \(A_{i-1}\) 时,我们的操作为(记 \(B=|A_{i-1}|\) ):
注意到操作1相当于新增一个单点,而操作2则至少会将 \(i\) 减少一半。因此每次我们遍历 \(\ge B\) 的所有有值的 \(f_i\) 进行更新即可。由于每被遍历一次至少有 \(i\gets\frac i2\) ,因此至多遍历 \(\mathcal O(n\log V)\) 次。用map维护,复杂度为 \(\mathcal O(n\log n\log V)\) 。
F Fraction of Fractal
平面图连通块个数问题联想到欧拉公式:点-边+面=连通块个数+1。分别求出点,边和面的个数即可。
点是容易求的。对于边,只需维护分别维护水平边和竖直边的数量。麻烦在于面。
题目有性质:初始时图联通。于是可以得到初始时的面个数。难点在于新增的面如何求出。不过注意到如果该图形上下拼接或左右拼接都能形成连通块,那么答案就是1。于是只需考虑左右拼接形成连通块从而产生新的面的情况(上下的同理)。发现如果 \(c\) 为左右拼接时边界新产生的边数,那么新产生的面数就是 \(\max(c-1,0)\) 。
每次分形等价于做一次线性变换,使用矩阵快速幂优化即可。
复杂度为 \(\mathcal O(\log n)\) 。
AGC004
C
有点意思的构造题。虽然nt的我完全没有想出来
很难说明这个构造是怎么想到的,大概是因为保证了边界上不会有格子?总之,将第一张图第一列以及所有奇数行涂色,然后将第二张图最后一列以及所有偶数行涂色,最后对于两张图再将给出的公共部分涂色即可。
D
首先不难发现需要将 \(1\) 号城市的目的地修改为自己,即形成一个自环。接下来问题转化为给出一棵内向树,但要求最深深度不超过 \(k\) ,每次操作为改变某个点的父亲,求最少操作次数。冷静下不难发现如此贪心策略:即从深到浅进行考虑,一旦发现某个子树的最深深度即将超过 \(k\) 就将其连到 \(1\) 下方。
于是问题在 \(\mathcal O(n)\) 的复杂度内得以解决。
E
运用相对运动的思想,可以将问题看作由出口去接机器人。不过出口会自带一个框,初始时的框就是整个网格,然后框会随着出口的移动而移动。一个机器人一旦超出框就G了。
如果要贪心之类的话可以发现非常困难。于是只能考虑dp了。记 \(f_{a,b,c,d}\) 表示从初始到现在出口向上走的最远距离为 \(a\) ,向下走的最远距离为 \(b\) ,向下走的最远距离为 \(c\) ,向下走的最远距离为 \(d\) 时最多能接到多少机器人。这些信息能指示出哪些位置的机器人已经G了或已经被拯救了。转移时枚举向上下左右四个方向能否扩展即可。
复杂度为 \(\mathcal O(n^4)\) 。
F
可能非常牛逼的题??
先考虑树的情况。
首先我们要创造性地想到将树进行二分图染色,那么每次修改相当于是要求边两端颜色不同然后交换两端的颜色。最终要求是黑点到白点位置上,白点到黑点位置上。可发现黑点和白点的个数都不会改变,因此如果黑白点个数不相等直接判无解即可。接下来我们对每条边考虑贡献:对于一条边,不妨设其对应子树内有 \(a\) 个黑点和 \(b\) 个白点,那么我们至少需要的操作次数就是 \(|a-b|\) ,因为要求黑白点个数相等。容易发现每条边的下界是可以同时取到的,因此答案就是下界之和。
再考虑偶环的情况。
假设这条边会操作 \(x\) 次。然后根据前面树的做法,问题可转化为最小化若干绝对值之和。取中位数即可取到最小。
最后考虑奇环的情况。
这条边唯一的贡献就是将黑点数量 \(-2/+2\) ,于是该边的操作次数就是整张图的黑白点之差 \(/2\) 。确定了这一点后跑树的做法即可。
AGC005
D
对于这类排列计数问题,一种经典的想法是将其对应到一张图上进行思考。即每个排列会对应到一张 \(n\times n\) 的01网格上,网格上 \((x,y)\) 位置是 \(1\) 当且仅当 \(p_x=y\) 。那么现在相当于我ban掉了所有 \(|x-y|=k\) 的点,求排列个数。
容易联想到容斥。在被ban掉的格子中选择 \(i\) 个点的方案数为 \(f_i\) ,对应容斥系数为 \((-1)^i\) 。不过注意到同一行/同一列被ban掉的点不能被同时选择,于是对同行或同列的点连边,问题变为一个若干条链形成的图中大小为 \(i\) 的独立集有多少个。dp即可。
F
考虑每个点对答案的贡献。列出柿子后减法卷积即可。
AGC006
B
小清新构造题。观察发现若某一层一个数出现两次且相邻,那么在上面的层中其仍然会在这两个相邻位置出现。于是只需要满足在倒数第二层中 \(n-1,n\) 或 \(n,n+1\) 两个位置出现给定的 \(x\) 即可。
C
根据题意列出柿子,然后观察可发现其本质是交换差分数组中的两个数。
D
B题的checker。
对于这类仅由大小关系决定最终答案问题都可以考虑二分答案 \(x\) ,然后将 \(\ge x\) 的看作 \(1\) ,将 \(<x\) 的看作 \(0\) ,然后考察最终是 \(0/1\) 。根据B题的思考,我们只需要找到最靠近 \(n\) 的长度超过 \(1\) 的连续全 \(0/1\) 段即可,答案就是该段的值。
E
首先有这样的观察:任何一列内部的数自始至终不会有任何变化。且最终情况下要么保持原顺序要么是原顺序倒过来。
于是可将三行压为一行:给每一列分配一个数 \(x\) ,该数的绝对值是该列中最大的数 \(/3\) ,符号为正当且仅当该列仍然保持原顺序。那么每次操作为选择一个位置 \(i\) ,然后交换 \(x_i,x_{i+2}\) ,最后将 \(x_i,x_{i+1},x_{i+2}\) 的符号全部取反。目标是序列 \(1,2,3,\cdots,n\) 。
可发现奇数位置和偶数位置间唯一的影响在于符号。进一步地,我们可以将奇偶性相同的两个位置 \(i,j\) 的符号同时取反,具体做法为找到 \(i-1,j+1\) ,然后将 \(j+1\) 处的数一步步地挪到 \(i+1\) ,然后交换 \(i-1,i+1\) ,最后再挪回 \(j+1\) ;之后再将 \(i-1\) 处的数一步步地挪到 \(j-1\) ,然后交换 \(j-1,j+1\) ,最后再挪回 \(i-1\) 。于是偶数位置交换对奇数位置符号的贡献可以是 和偶数位置上逆序对奇偶性相同的任何数 ,奇数对偶数同理。此后我们就将奇数位置和偶数位置分开来了。
分开后就是每次只能交换相邻两个数的平凡的排序了。注意每次交换会改变符号。最终判下负数的个数是否能恰好和贡献相同即可。
F
转化为图论问题:若有边 \(x\to y,y\to z\) 则连边 \(z\to x\) 。
对每个若连通块考虑。三元环启示我们将图进行三染色,然后有三种情况:
- 染色失败。则该图最终会连成完全图,即任意两个点均有连边。
- 染色成功,然而仅有两种颜色。此刻不会新增任何边。
- 染色成功,且三种颜色均有。最终的边会变为任意一个颜色的点会向下一个颜色的所有点连边。
于是dfs后简单计数即可。
AGC040
A ><
冷静思考可以发现每个位置可以填的最小值是左侧连续小于号的个数和右侧连续大于号的个数的较大值。扫一遍即可。
B Two Contests
对于两个区间\(A,B\) ,假设\(A\) 包含\(B\) ,那么\(A\) 一定和\(B\) 被分在一个组中,因为\(A\) 放在\(B\) 所在的组中不会影响该组的答案,而放到另一组中可能会减小答案。因此可以忽略所有这样的\(A\) ,将剩下区间按左端点排序,那么右端点也一定有序。此时最优方案一定是一个前缀+一个后缀。预处理后缀左端点max和右端点min,枚举分界点即可快速得到答案。注意有特殊情况,即某个区间单独成一组。
对于区间问题从两个相包含的区间入手是一种很不错的方式。
C Neither AB nor BA
考虑将序列编号为奇数的染黑,其他的染白。那么每次操作必然是一黑一白两个位置。我们将黑色位置的A变为B,B变为A,此时题意可以转化为除了AA,BB两种子串外其他长度为2的均可删除。容易发现不满足要求的串当且仅当A/B的总出现次数超过\(\frac n2\) ,因此直接容斥计数即可。
积累下本题的特殊做法。
D Balance Beam
对于一种已经确定的排列顺序,必然存在一个分界点使得Bob在分界点左侧出发一定被抓住,在其右侧出发一定不会被抓。
为了使得这个问题更加形象化,我们考虑建立纵坐标代表时间,横坐标代表位移的图像,那么Alice和Bob的图像就是一个从\((0,0)\) 出发,分别到达\((n,s_a),(n,s_b)\) 的分为\(n\) 段的折线(\(s_a=\sum_{i=1}^na_i,s_b=\sum_{i=1}^nb_i\)),而Alice会抓住Bob当且仅当两条折线存在交点。现在,我们将Bob的折线向下平移至即将和Alice的折线没有交点(但是仍然有交点)的位置,此时设折线和\(x\) 轴的交点为\((k,0)\) ,我们现在需要最大化\(k\) 。
对于一条从\((k,0)\) 出发,先沿着Bob的折线走,然后再沿着Alice的折线走的折线,其终点一定是\((n,s_a)\) 。我们假设\((k,0)\) 所在的石块为\(p\) ,需要尽可能地最大化折线的增长速度就能得到最大的\(k\) 。观察可以发现第\(i\) 段的斜率最大为\(\max (a_i,b_i)\) ,因此我们可以将石块按照\(\max (a_i,b_i)\) 从小到大进行排序,二分找到最大的\(t\) 满足\(t\) 处的\(\max (a_i,b_i)\) 后缀和不小于\(s_a-b_p\) 。(为什么一定可以取到最大?其实只需要先放\(b_i>a_i\) 的石块,然后再放\(a_i>b_i\) 的石块即可。)至于此时\(k\) 的具体值可以通过简单的计算得出。然后枚举\(1\sim n\) 作为\(p\) ,不断取\(\max\) 即可。
本题启示我们当问题过于繁琐时可以通过画图来使问题具象化,方便思考。
E Prefix Suffix Addition
题中所述的两种操作事实上可以看做对任意一个区间加上一个单调不降/不增的序列,因为我们可以在前面添加0。
然后可以发现对于其中一种操作,通过调整一定可以使得覆盖的范围互不相交,因为对于相交的部分我们可以直接叠加到一个操作上,由于不降序列+不降序列仍然不降,因此这样一定满足条件。
设\(b_i,c_i\) 分别表示1操作和2操作对位置\(i\) 的贡献(\(b_i,c_i\ge 0\))。显然必须满足\(b_i+c_i=a_i\) 。我们需要将\(b,c\) 划分为尽量少的单调不降/不增连续段。强制钦定\(a_0=a_{n+1}=0\) ,那么在\(b_i,c_i\) 都确定后的答案就是\(\sum_{i=0}^n([b_i>b_{i+1}]+[c_i<c_{i+1}])\) 。最小化这个东西即可。
考虑dp。令\(f_{i,j}\) 表示考虑前\(i\) 个位置且\(b_i=j\) 时的贡献。那么有转移:
根据转移方程容易发现当\(i\) 不变时,\(f_{i,j}\) 随着\(j\) 不增。同时一定有\(f_{i,0}\le f_{i,a_i}+2\) 。因此我们只需要维护\(f_{i,x}=k\) 的\(x\) 的范围,由于不同的\(x\) 最多3种,因此直接转移即可。复杂度\(\mathcal O(n)\) 。具体实现时二分会更好写,不过复杂度会多个$\log $ 。
F Two Pieces
我们考虑用二元组\((x,d)\) 表示两个点的位置信息,其中\(x\) 表示靠前的点的位置,\(d\) 表示两个棋子之间的距离。那么对应于原操作,有以下三种操作:
- \((x,d)\leftarrow (x+1,d+1)\)
- \((x,d)\leftarrow (x,d-1)(d\ge 2)\)
- \((x,d)\leftarrow (x,0)\)
注意第二种情况必须保证\(d\ge 2\) ,这是因为如果\(d=1\) 时执行2操作效果会和3操作相同,而这样处理后我们便不再需要对于位置计数,而只需要对于操作序列计数了。
最终到达的状态为\((B,B-A)\) 。容易发现1操作必须恰好进行\(B\) 次。而后我们可以枚举2操作的次数为\(k\) ,还剩下\(N-B-k\) 次操作3。在只考虑1,2两种操作情况下,我们需要时刻保证\(d\ge 1\) (初始时刻除外)。这种情况下的方案数可以用类似求卡特兰数的方法求出方案数,结果为\(\dbinom {B+k-1}k-\dbinom{B+k-1}B\) 。
现在我们只需要将\(N-B-k\) 次3操作插入这个操作序列即可。考虑到在\(i\) 处进行一次3操作,那么\(\forall t\in[i,B+k]\ \ d_t\leftarrow d_t-d_i\) 。因为我们要保证\(d_t\ge 1\) ,因此\(\forall t\in[i,B+k]\ \ d_t>d_i\) ,即能插在\(i\) 操作后当且仅当不存在\(j>i\) 使得\(d_j\le d_i\) 。而观察到\(d\) 每次的变化量只有1,因此对于\(d_t=x\) (\(x\) 为某定值)的所有\(t\) ,我们只能在最大的\(t\) 处插入若干3操作。现在我们的状态是\((B,B-k)\) ,需要将它变为\((B,B-A)\) 。假设我们在\(c_1,c_2,\cdots ,c_p\) 这些位置进行3操作,那么最终状态的变化为\(\max_i d_{c_i}\) ,因此\(\max_i d_{c_i}=(B-k)-(B-A)=A-k\) ,这意味着我们需要在\(d_t=A-k\) 的最大的\(t\) 处进行至少一次操作。不妨设\(N-B-k>0\) (\(N-B-k=0\) 的情况是trivial的,合法当且仅当\(k=A\) ),还剩下\(N-B-k-1\) 次操作可以任意地放入\(d_t=0\sim A-k\) 的最大的\(t\) 处,即将\(N-B-k-1\) 个球放入\(A-k+1\) 个盒子的方案数,为\(\dbinom {N+A-B-2k-1}{A-k}\) 。
将两部分方案乘起来,枚举\(k\) 求和即可。复杂度\(\mathcal O(n)\) 。


