CSP-S2021题解
廊桥分配
description
机场分国内区和国际区，分别有\(m_1,m_2\) 架飞机会到来，每架飞机停在机场的时间为\([a_i,b_i]\) 。每架飞机来到机场后会选择在廊桥/远机位。飞机会优先停靠廊桥，而廊桥使用先到先得，即如果某架飞机到达时存在空闲的廊桥则会停靠，否则停靠远机位。现在总共\(n\) 个廊桥，要求进行合理的分配使得停靠廊桥的飞机尽量多。\(1\le n,m_1+m_2\le 10^5\)
solution
将国内区和国际区分开考虑，最后再将答案合并。容易发现对于一架飞机如果在有\(i\) 个廊桥时找到了位置，那么有\(>i\) 个廊桥时它也能找到位置并且位置不变。因此从小到大枚举廊桥个数，每次根据先到先得的原则选择不相交的区间即可。使用set进行维护，复杂度\(\mathcal O(n\log n)\) 。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m[2],res[2][N];
set<pair<int,int> >s[2];
int main()
{
scanf("%d%d%d",&n,&m[0],&m[1]);
for(bool o:{0,1})
for(int i=1,l,r;i<=m[o];++i)
scanf("%d%d",&l,&r),s[o].insert(make_pair(l,r));
for(bool o:{0,1})
for(int i=1;i<=n;++i)
{
res[o][i]=res[o][i-1];
if(s[o].empty())continue;
int pre=0;
while(1)
{
auto p=s[o].upper_bound(make_pair(pre,0));
if(p==s[o].end())break;
++res[o][i];pre=(*p).second;
s[o].erase(p);
}
}
int ans=0;
for(int i=0;i<=n;++i)ans=max(ans,res[0][i]+res[1][n-i]);
printf("%d\n",ans);
return 0;
}
括号序列
description
以如下的方式定义“超级括号序列”：
()、(S)均是符合规范的超级括号序列，其中S表示任意一个仅由不超过 k 个字符*组成的非空字符串（以下两条规则中的S均为此含义）；- 如果字符串
A和B均为符合规范的超级括号序列，那么字符串AB、ASB均为符合规范的超级括号序列，其中AB表示把字符串A和字符串B拼接在一起形成的字符串； - 如果字符串
A为符合规范的超级括号序列，那么字符串(A)、(SA)、(AS)均为符合规范的超级括号序列。 - 所有符合规范的超级括号序列均可通过上述 3 条规则得到。
现在需要对一个包含且仅包含(,),?,*的字符串\(|S|\) 求出有多少中填法使得其得到的字符串是一个超级括号序列。
有模数。\(|S|\le 500\) 。
solution
区间dp即可。三种规则生成的字符串都是互不重复的，因此对三种规则分别转移即可。直接转移会在第二个规则时将\(\texttt{()()()}\) 这种情况多次计算，因此在区间\([l,r]\) 枚举断点\(k\) 时必须钦定\([l,k]\) 这段区间\(l\) 处的左括号和\(k\) 处的右括号匹配即可，需要新增一种dp状态。再使用前缀和进行优化就能做到\(\mathcal O(n^3)\) 了。
code
#include<bits/stdc++.h>
using namespace std;
const int N=505,mod=1e9+7;
inline int add(int x,int y){return x+y>=mod?x+y-mod:x+y;}
inline int dec(int x,int y){return x-y<0?x-y+mod:x-y;}
inline void inc(int&x,int y){x=x+y>=mod?x+y-mod:x+y;}
int n,k,f[N][N],s[N],g[N][N],sum[N][N];char ch[N];
inline bool ok(int l,int r){return s[r]-s[l-1]==0;}
inline bool okl(int p){return ch[p]=='?'||ch[p]=='(';}
inline bool okr(int p){return ch[p]=='?'||ch[p]==')';}
inline int S(int pl,int pr,int r){return dec(sum[pl][r],sum[pr+1][r]);}
int main()
{
scanf("%d%d",&n,&k);
scanf("%s",ch+1);
for(int i=1;i<=n;++i)s[i]=s[i-1]+(ch[i]=='('||ch[i]==')');
for(int len=2;len<=n;++len)
for(int l=1,r=l+len-1;r<=n;++l,++r)
{
int&d=f[l][r],&e=g[l][r];
if(len==2&&okl(l)&&okr(r))++d,++e;
if(3<=len&&len<=k+2&&okl(l)&&okr(r)&&ok(l+1,r-1))++d,++e;
for(int p=l,q=p;p<r;++p)
{
inc(d,1ll*g[l][p]*f[p+1][r]%mod);
q=max(q,p);
while(q<r&&ok(q+1,q+1))++q;
if(p+2<=r&&p<q)inc(d,1ll*g[l][p]*S(p+2,min({r,q+1,p+k+1}),r)%mod);
}
if(len>2&&okl(l)&&okr(r))
{
int res=0;
inc(res,f[l+1][r-1]);
for(int t=1;t<=k&&l+t<r;++t)
if(ok(l+1,l+t))inc(res,f[l+t+1][r-1]);
else break;
for(int t=1;t<=k&&r-t>l;++t)
if(ok(r-t,r-1))inc(res,f[l+1][r-t-1]);
else break;
inc(d,res),inc(e,res);
}
sum[l][r]=add(sum[l+1][r],d);
}
printf("%d\n",f[1][n]);
return 0;
}
回文
description
有一个长度为\(2n\) 的双端队列，其中\(1\sim n\) 都恰好出现了2次。现在要求每次操作从左侧/右侧弹出一个数依次排列形成序列\(b\) ，要求\(b\) 是回文的。如果无法做到，输出-1，否则输出字典序最小的方案数。\(n\le 5\times 10^5\)
solution
显然必然存在一个分界点满足分界点左侧都是从左端依次弹出，分界点右侧都是从右端依次弹出。枚举这个分界点，然后左右两侧的数各形成一个栈。每次需要从栈顶取出元素\(x\) ，那么必须满足和\(x\) 值相同的元素必须位于某个栈的栈底。然后将这两个数都删去继续做即可。由于要求字典序最小，因此每次需要贪心的选择。然而现在仍然是\(\mathcal O(n^2)\) 的。注意到两个栈的栈顶都是确定的，因此对应的栈底也有强限制，这使得合法的分界点只有4个，分别枚举做即可。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n,a[N],s[N],t[N];bool ans[N],fl,res[N];
inline void work(int p)
{
int x=0,y=0;
for(int i=1;i<=p;++i)s[++x]=a[i];
for(int i=2*n;i>p;--i)t[++y]=a[i];
int c=1,d=1;
for(int i=1;i<=n;++i)
{
int p1=i,p2=2*n-i+1;
if(c<x&&s[c]==s[x])res[p1]=res[p2]=0,++c,--x;
else if(c<=x&&d<=y&&s[c]==t[y])res[p1]=0,res[p2]=1,++c,--y;
else if(c<=x&&d<=y&&t[d]==s[x])res[p1]=1,res[p2]=0,++d,--x;
else if(d<y&&t[d]==t[y])res[p1]=res[p2]=1,++d,--y;
else return;
}
fl=1;bool ok=0;
for(int i=1;i<=2*n;++i)
if(res[i]<ans[i]){ok=1;break;}
else if(res[i]>ans[i]){ok=0;break;}
if(ok)for(int i=1;i<=2*n;++i)ans[i]=res[i];
}
int main()
{
int T=read();
while(T-->0)
{
n=read();
for(int i=1;i<=2*n;++i)a[i]=read(),ans[i]=1;
int p1=0,p2=0;
for(int i=2;i<=2*n;++i)if(a[i]==a[1]){p1=i;break;}
for(int i=1;i<2*n;++i)if(a[i]==a[2*n]){p2=i;break;}
fl=0;work(p1),work(p1-1);work(p2),work(p2-1);
if(!fl){puts("-1");continue;}
for(int i=1;i<=2*n;++i)putchar(ans[i]?'R':'L');puts("");
}
return 0;
}
交通规划
description
有一个由\(n\) 条横直线，\(m\) 条纵直线互相相交形成的网格图，网格中的边有边权。
现在从网格边界向外延伸的\(2(n+m)\) 条射线中，有\(k\) 条出现了颜色为黑/白的点，并且一直它和最近的网格点之间的边权大小。现在需要给网格点进行染色，使得左右两端染色不同的边的边权之和最小。
\(n,m\le 500,\sum k\le 50\)
solution
\(k=2\) 的时候容易发现是最小割。根据狼抓兔子的那套理论，可以将平面图最小割转化为对偶图最短路。
\(k>2\) 的时候考虑其本质是什么，如下图所示：
对于相邻且颜色不同的点我们需要用割边将其隔开，而注意到一条割边可以分隔两对这样的点，因此对这些间隔（图中绿色部分）一一匹配可以达到最优。而匹配的代价就是原图最小割，即对偶图上的最短路。
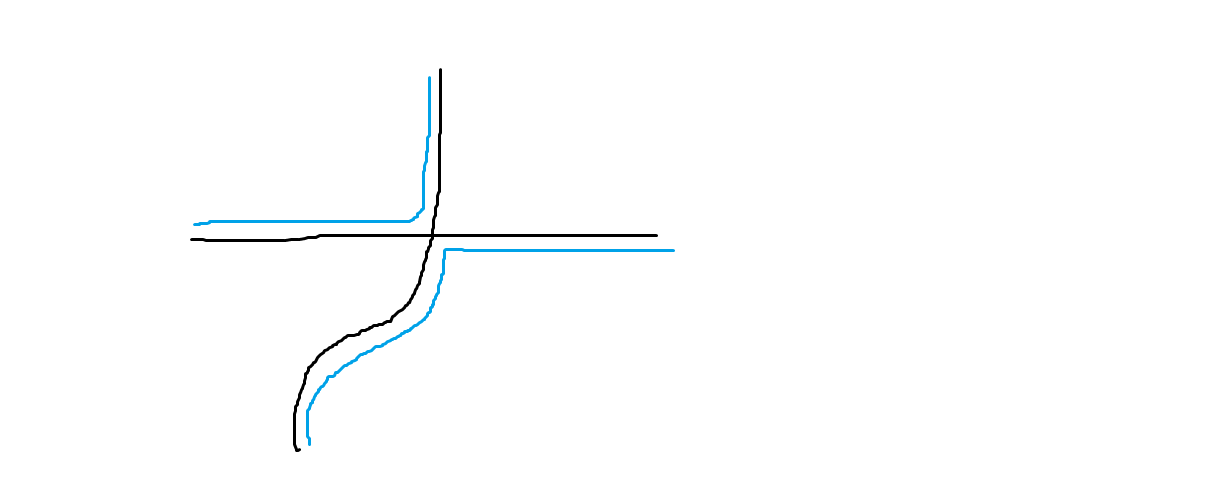
而对于两条割线相交的情况（上图黑线），我们可以用蓝线进行代替，代价相同且效果相同。即我们可以通过调整使得最优解的任意两条割线都不相交。
因此对于每组询问只需要处理出间隔间的最短路，然后区间dp即可。dp转移时只需考虑左侧端点的匹配节点就行。
时间复杂度：\(\mathcal O(k^3+knm\log nm)\) 。
code
#include<bits/stdc++.h>
using namespace std;
const int N=505,inf=0x3f3f3f3f;
int n,m,T,k;
int tot=1,fi[N*N],ne[N*N*4],to[N*N*4],w[N*N*4],op[N*4];
struct node{int pos,val,c;}t[N];
inline int id(int x,int y){return x*(m+1)+y+1;}
inline void add(int x,int y,int s)
{
ne[++tot]=fi[x],fi[x]=tot,to[tot]=y,w[tot]=s;
ne[++tot]=fi[y],fi[y]=tot,to[tot]=x,w[tot]=s;
}
int key[N*8],dis[N*N],res[105][105],f[105][105];bool done[N*N];
inline int gp(int x)
{
if(x<=m)return id(0,x);x-=m;
if(x<=n)return id(x,m);x-=n;
if(x<=m)return id(n,m-x);x-=m;
return id(n-x,0);
}
inline void dij(int S)
{
typedef pair<int,int> pii;
priority_queue<pii,vector<pii>,greater<pii> >q;
fill(dis+1,dis+id(n,m)+1,inf);
fill(done+1,done+id(n,m)+1,0);
q.push(make_pair(dis[S]=0,S));
while(!q.empty())
{
int u=q.top().second;q.pop();
if(done[u])continue;done[u]=1;
for(int i=fi[u];i;i=ne[i])
{
int v=to[i];
if(dis[v]>dis[u]+w[i])
{
dis[v]=dis[u]+w[i];
q.push(make_pair(dis[v],v));
}
}
}
}
inline void work()
{
scanf("%d",&k);int cc=0;
for(int i=1;i<=k;++i)
scanf("%d%d%d",&t[i].val,&t[i].pos,&t[i].c);
sort(t+1,t+k+1,[&](const node&x,const node&y){return x.pos<y.pos;});
for(int i=1;i<=k;++i)
{
int now=t[i].pos;
w[op[now]]=w[op[now]^1]=t[i].val;
int j=i==k?1:i+1;
if(t[i].c==t[j].c)continue;
key[++cc]=gp(t[i].pos);
}
if(!cc)puts("0");
else
{
for(int i=1;i<=cc;++i)
{
dij(key[i]);
for(int j=1;j<=cc;++j)
res[i][j]=dis[key[j]];
}
for(int i=1,j=cc+1;i<=cc;++i,++j)key[j]=key[i];
cc<<=1;int mm=cc>>1;
for(int i=1;i<=cc;++i)f[i][i-1]=0;
for(int len=2;len<=cc;len+=2)
for(int l=1,r=l+len-1;r<=cc;++l,++r)
{
int&d=f[l][r];d=inf;
for(int t=l+1;t<=r;t+=2)
d=min(d,f[l+1][t-1]+f[t+1][r]+res[l>mm?l-mm:l][t>mm?t-mm:t]);
}
int ans=inf;
for(int i=1,j=mm;j<=cc;++i,++j)ans=min(ans,f[i][j]);
printf("%d\n",ans);
}
for(int i=1;i<=k;++i)
{
int now=t[i].pos;
w[op[now]]=w[op[now]^1]=0;
}
}
int main()
{
scanf("%d%d%d",&n,&m,&T);
for(int i=1;i<n;++i)
for(int j=1,t;j<=m;++j)
scanf("%d",&t),add(id(i,j-1),id(i,j),t);
for(int i=1;i<=n;++i)
for(int j=1,t;j<m;++j)
scanf("%d",&t),add(id(i-1,j),id(i,j),t);
for(int i=1;i<=m;++i)add(id(0,i-1),id(0,i),0),op[i]=tot;
for(int i=1;i<=n;++i)add(id(i-1,m),id(i,m),0),op[m+i]=tot;
for(int i=1;i<=m;++i)add(id(n,m-i+1),id(n,m-i),0),op[m+n+i]=tot;
for(int i=1;i<=n;++i)add(id(n-i+1,0),id(n-i,0),0),op[m+n+m+i]=tot;
while(T--)work();
return 0;
}
