后缀数组原理浅析（转载自tqx）

原博客链接

一、概述

后缀数组(\(SA，Suffix\ Array\))，是将字符串的所有后缀排序得到的数组，主要包括两个数组：

\(sa[i]\)：将所有后缀按字典序排序后第\(i\)小的后缀的开头位置

\(rk[i]\)：表示从第\(i\)个字符开始的后缀（我们将它称为后缀\(i\)）的字典序排名

它们满足\(sa[rk[i]]=rk[sa[i]]=i\)

一个例子(搬迁自后缀数组——处理字符串的有力工具罗穗骞)：

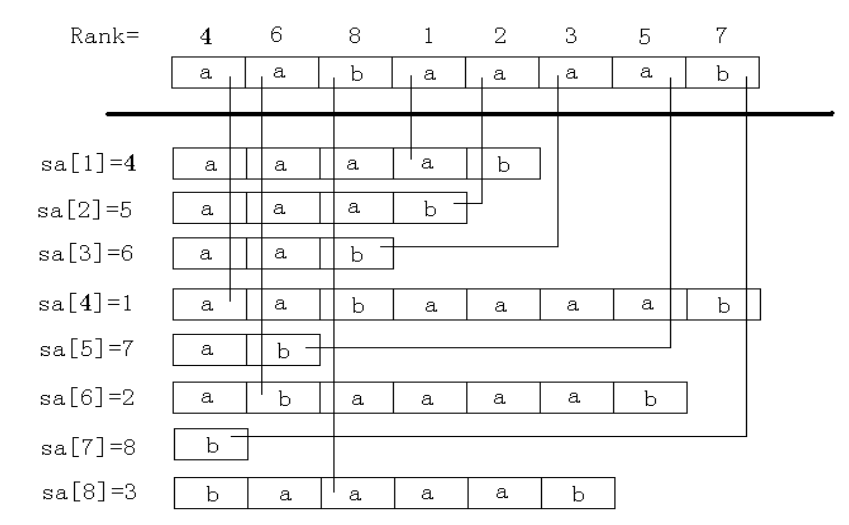
如果我们能快速求出\(sa\)与\(rk\)，那么我们能利用它们完成很多字符串题目，我们接下来介绍后缀数组的求法，然后再介绍一些常见应用：

二、后缀数组的求法

倍增求法

最常见的一种求法，复杂度为\(\mathcal O(nlog(n))\)，这个算法的核心就是利用倍增的思想。

思想

首先我们先按照每个后缀的第一个字符对后缀进行排序，这相当于将这个字符串的每个字符进行排序

显然，这样做会出现排名相同的后缀，接下来我们就要对这些字符串的第二位进行排序了。我们再排序一次吗？事实上，我们已经比较过了：因为后缀\(i\)的第\(2\)个字符正是后缀\(i+1\)的第\(1\)个字符，也就是说，后缀的第二个字符的排序就是它的下一个后缀的第一个字符的排序，利用这个排序作为第二关键字，我们就能得到前两位的排序了

以此类推，现在我们知道了前两位的排序，自然也就知道了第\(3-4\)位的排序，于是用同样的方法就能求出前\(4\)位的排序，如此倍增下去，直到每一个后缀的排名都不相同，我们就完成了排序。

对双关键字进行排序这件事，我们可以通过基数排序做到\(\mathcal O(n)\)，因此算法的复杂度是\(\mathcal O(nlog(n))\)

那么具体如何实现呢？我个人认为后缀数组的代码对初学者十分不友好，因此我们一点一点地来讲。

代码理解

在这个过程中，我们用\(s[i]\)表示原字符串第\(i\)位，\(rk[i]\)表示按第一关键字排序得到的结果，一开始我们排序的是第一个字母，那么\(rk[i]\)就是\(s[i]\)

for(int i=1;i<=n;++i)
	rk[i]=s[i],++c[rk[i]];//刚开始第一关键字就是该后缀的第一个字母 
for(int i=2;i<=S;++i)
	c[i]+=c[i-1];
for(int i=n;i>=1;--i) sa[c[rk[i]]--]=i;

这里\(S\)是目前排名集合的大小，这里我们用桶排序的思想，用\(c[x]\)表示排名是\(x\)的字符串个数，做个前缀和之后\(c[x]\)表示排名\(\le x\)的字符串个数，然后我们就可以求出\(sa\)了，在出现相同排名时，我们现在不关心它们的内部排名，就直接让位置靠后的字符串排名较小，最后一个直接排名为\(c[rk[i]]\)，然后将它\(--\)作为下一个排名相同的字符串的排名以保证排名互不相同

接着开始倍增，枚举\(k\)表示目前我们已经知道前\(k\)位的排序，想要推出前\(2k\)位的排序

int num=0;
for(int i=n-k+1;i<=n;++i) y[++num]=i;
for(int i=1;i<=n;++i)
	if(sa[i]>k) y[++num]=sa[i]-k;//y[i]：第二关键字排名为i位的后缀的起始位置

这一段代码是求出第二关键字，即第\(k+1-2k\)位的字典序排序，我们用\(y[i]\)表示第二关键字排名第\(i\)位的后缀的其起始位置，对于后缀\(n-k+1-n\)，它们没有\(k+1-2k\)位的东西，因此它们直接排在最前面，紧接着枚举第一关键字的排名，被先枚举到的\(sa[i]\)意味着后缀\(sa[i]-k\)的第二关键字排名靠前，因此我们按序加入\(y\)中。

for(int i=1;i<=S;++i) c[i]=0;
for(int i=1;i<=n;++i) c[rk[i]]++;
for(int i=2;i<=S;++i) c[i]+=c[i-1];
for(int i=n;i>=1;--i)
	sa[c[rk[y[i]]]--]=y[i],y[i]=rk[i];
//桶排序优先保证了第一关键字的排名，因为是从后往前考虑y所以说相对靠后的是第二关键字排行靠后的

接下来开始基数排序，我们还是先按\(rk\)放在桶中，但这次对于\(rk\)相同的后缀我们不能随意排序了，要第二关键字靠后的排在后面，于是我们从后往前枚举\(y[i]\)，这样先枚举到的第二关键字一定更大，于是给它较大的排名。\(y[i]=rk[i]\)则是我们接下来要重新计算\(rk\)，但会用到之前的\(rk\)，于是我们直接用\(y\)保存下来。

rk[sa[1]]=num=1;
for(int i=2;i<=n;++i){
	if(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])						             rk[sa[i]]=num;
	else rk[sa[i]]=++num;
}
if(num==n) return ;
S=num;

接下来我们利用\(sa\)重新计算\(rk\)，这时如果两个后缀的两个关键字都相同，那么直接使用\(num\)，否则\(num++\)，当\(num=n\)时所有后缀的排名互不相同，于是我们就完成了排序。

洛谷模板题代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
char s[N];
int rk[N],y[N],sa[N],n,c[N],S=122;
//千万牢记：sa[i]是当前排第i位的后缀的起始位置 
//rk[i]是从i开始的后缀的排名 
inline void getsa(){
	for(int i=1;i<=n;++i)
		rk[i]=s[i],++c[rk[i]];//刚开始第一关键字就是该后缀的第一个字母 
	for(int i=2;i<=S;++i)
		c[i]+=c[i-1];
	for(int i=n;i>=1;--i) sa[c[rk[i]]--]=i;
	for(int k=1;k<=n;k<<=1){//开始倍增 
		int num=0;
		for(int i=n-k+1;i<=n;++i) y[++num]=i;
		for(int i=1;i<=n;++i)
			if(sa[i]>k) y[++num]=sa[i]-k;//y[i]：第二关键字排名为i位的后缀的起实位置 
		for(int i=1;i<=S;++i) c[i]=0;
		for(int i=1;i<=n;++i) c[rk[i]]++;
		for(int i=2;i<=S;++i) c[i]+=c[i-1];
		for(int i=n;i>=1;--i)
			sa[c[rk[y[i]]]--]=y[i],y[i]=0;
		//桶排序优先保证了第一关键字的排名，因为是从后往前考虑y所以说相对靠后的是第二关键字排行考后的
		swap(rk,y);rk[sa[1]]=num=1;
		for(int i=2;i<=n;++i){
			if(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])
				rk[sa[i]]=num;
			else rk[sa[i]]=++num;
		}
		if(num==n) return ;
		S=num;
	}
}
int main(){
	scanf("%s",s+1);
	n=strlen(s+1);
	getsa();
	for(int i=1;i<=n;++i) printf("%d ",sa[i]);
	return 0;
}

DC3算法与SA-IS算法

二者都是\(\mathcal O(n)\)的算法，博主不太会，不过一般来说倍增算法就够用了，学习这两种算法，可以参考[后缀数组——处理字符串的有力工具罗穗骞](后缀数组——处理字符串的有力工具罗穗骞)学习\(DC3\)，参考诱导排序与SA-IS算法学习\(SA-IS\)

三、后缀数组的应用

最长公共前缀\(LCP\)

这是后缀数组最重要的应用之一，我们定义\(LCP(i,j)\)表示后缀\(sa[i]\)与后缀\(sa[j]\)的最长公共前缀。

为了求解它，我们给出一些性质
- \(LCP(i,j)=LCP(j,i)\)
- \(LCP(i,i)=n-sa[i]+1\)
这两条性质是显然的，于是我们可以只用考虑\(i<j\)的情况了。
- \(LCP\ Lemma\)：\(LCP(i,j)=min(LCP(i,k),LCP(k,j))(1\le i\le k\le j\le n)\)
  
  证明：令\(t=min(LCP(i,k),LCP(k,j))\)，那么\(LCP(i,k)\le t,LCP(k,j)\le t\)，
  
  于是后缀\(sa[i]\)与后缀\(sa[k]\)的前\(t\)个字符完全相同，后缀\(sa[k]\)与后缀\(sa[j]\)的前\(t\)个字符相同，故后缀\(sa[i]\)与后缀\(sa[j]\)的前\(t\)个字符相同，故\(LCP(i,j)\ge t\)。
  
  同时因为如果\(LCP(i,j)=q>t\)，那么\(i,j\)的前\(q\)个字符相等，因为\(t=min(LCP(i,k),LCP(k,j))\)，所以要么\(sa[i][t+1]\)(表示后缀\(sa[i]\)的第\(t+1\)位)\(<\)\(sa[k][t+1]\)，要么\(sa[k][t+1]\)\(<sa[j][t+1]\)，并且\(sa[i][t+1]\le sa[k][t+1]\le sa[j][t+1]\)，所以\(sa[i][t+1]\not=sa[j][t+1]\)，与假设矛盾，所以\(LCP(i,j)=t\)
- \(LCP\ Theorem\)：\(LCP(i,j)=min(LCP(k-1,k))\ ,k\in(i,j]\)
  
  证明：有\(LCP\ Lemma\)：\(LCP(i,j)=min(LCP(i,i+1),LCP(i+1,j)\),然后继续拆下去即可证明。
于是，我们令\(height[i]=LCP(i,i-1),height[1]=0\)，那么只要求出\(height\)我们就能求出\(LCP\)了，如何求出\(height\)呢？

再令\(h[i]=height[rk[i]]\)，于是\(height[i]=h[sa[i]]\)，对\(h[i]\)，我们有一个重要定理：
- \(h[i]\ge h[i-1]-1\)
- 证明：首先我们假设\(sa[rk[i]-1]=j,sa[rk[i-1]-1]=k\)，于是\(h[i]=LCP(j,i),h[i-1]=LCP(k,i-1)\)，于是我们只需证明\(LCP(j,i)\ge LCP(k,i-1)-1\)
- 如果后缀\(k\)与后缀\(i-1\)首字母不同，那么\(LCP(k,i-1)-1=-1\)，那么无论\(h[i]\)是多少定理都一定成立
- 如果后缀\(k\)与后缀\(i-1\)首字母相同，那么分别去掉首字母后得到后缀\(k+1\)与后缀\(i\)，必有\(rk[k+1]\)也\(<rk[i]\)，于是\(LCP(k+1,i)=h[i-1]-1\)，对于字符串\(i\)，所有排名比它靠前的字符串中，与它相似度最高也就是\(LCP\)最大的一定是紧挨着它的字符串，即\(j\)，但我们已知\(k+1\)排在\(i\)前面并且\(LCP(k+1,i)=h[i-1]-1\)，那么必然有\(LCP(j,i)\ge LCP(k+1,i)=h[i-1]-1\)，即\(h[i]\ge h[i-1]+1\)
根据这一条定理，我们就可以直接枚举\(rk[i]\)然后从\(height[rk[i-1]]-1\)作为起始点求\(height[rk[i]]\)达到\(\mathcal O(n)\)求出所有\(height\)了：
```
int height[N],h[N];
inline void getheight(){
	int k=0;
	for(int i=1;i<=n;++i){
		if(rk[i]==1) continue;
		if(k) --k;
		int j=sa[rk[i]-1];
		while(j+k<=n&&i+k<=n&&s[j+k]==s[i+k]) ++k;
		height[rk[i]]=k;  
	}
	for(int i=1;i<=n;++i) printf("%d ",height[i]);
}
```

posted @ 2021-04-19 11:31 BILL666 阅读(118) 评论(0) 编辑收藏举报

刷新页面返回顶部

BILL666

相信自己，相信未来