WC2021题目略解
T1
solution
不会?完全没思路?那就来看看性质吧
如果\(x\to y\) 合法,那么\(y\to x\) 合法(自反性)
如果\(x\to y,y\to z\) 合法,那么\(x\to z\) 合法(传递性)
由此可知若将可以通过合法序列到达的点连边,形成的图一定是一个由若干团拼成的,而我们只需要找出这些团最后统计答案即可
考虑合法的括号序列是如何生成的?
- 空串合法
- \(A\)合法\(\to\) \((A)\)合法
- \(A,B\)合法\(\to\) \(AB\)合法
由此我们可以以\(()\)为基础,通过和合法串的拼接或在外面加括号实现任意合法括号序列的生成
\(()\)如何出现?
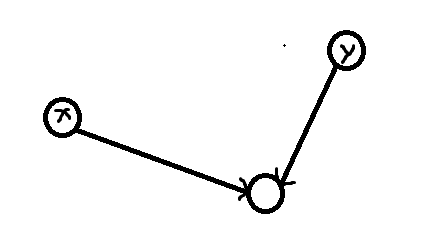
如图,两条黑边的括号类型是相同的,此时\(x\to y(y\to x)\)就是\(()\)
考虑合法串拼接,即\(x\to y\to z\) (其中\(y\to z\) 合法)
考虑在外面加括号,即\(a\to x\to y\to b\) (其中\(a\to x,b\to y\) 的边都是同类型的左括号)
在这两种生成方式中,不难发现和具体\(x\)如何到\(y\)没有关系,只关心是否可达
意即可以将\(x,y\)合并当作一个点处理
根据上面的思考不难看出\(x,y\)的合并可能会引出新的合并,而我们只需不断地这样合并直到没有合法点对,此时算法结束,所有点所在的团的编号已被求出
具体实现可以采用哈希表映射存边(括号类型是原象,边起点是象),用并查集模拟合并,用队列处理一次合并引发出的多次合并。另外,为保证复杂度,需使用启发式合并。
time complexity
\(\mathcal O(m\log m)\)
code
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
typedef pair<int,int> pii;
typedef long long ll;
unordered_map<int,int>mp[N];
inline int read()
{
int s=0,w=1; char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')w=-1;
for(;isdigit(ch);ch=getchar())s=(s<<1)+(s<<3)+(ch^48);
return s*w;
}
int fa[N],sz[N],n,m,k,cnt[N];
int fd(int x){return fa[x]==x?x:fa[x]=fd(fa[x]);}
queue<pii>q;
inline void mge(int x,int y)
{
x=fd(x),y=fd(y);
if(x==y)return;
if(sz[x]<sz[y])swap(x,y);fa[y]=x;
for(auto t=mp[y].begin();t!=mp[y].end();t++)
{
if(!mp[x].count(t->first))mp[x][t->first]=t->second,++sz[x];
else q.push(make_pair(t->second,mp[x][t->first]));
}
}
int main()
{
n=read(),m=read(),k=read();
for(int i=1,u,v,w;i<=m;++i)
{
u=read(),v=read(),w=read();
if(!mp[v].count(w))mp[v][w]=u,++sz[v];
else q.push(make_pair(mp[v][w],u));
}
for(int i=1;i<=n;++i)fa[i]=i;
while(!q.empty())
{
auto t=q.front();q.pop();
mge(t.first,t.second);
}ll ans=0;
for(int i=1;i<=n;++i)++cnt[fd(i)];
for(int i=1;i<=n;++i)ans+=1ll*cnt[i]*(cnt[i]-1)/2;
printf("%lld\n",ans);
return 0;
}
T2
solution
对于表达式\(E\) ,不妨建出其表达式树(为二叉树),它的特点如下
- 叶子节点表示操作数
- 非叶子节点代表一次运算,即对左右儿子进行一次\(>\) 或\(<\) 运算
设其根为\(rt\)
不难发现数组的每一位都是相对独立的,因此只用考虑\(m\)个数的情况,设它们为\(a_1,a_2,\cdots ,a_m\)
考虑到\(m\)很小,同时最终答案也必然在\(m\)个数中产生,我们不妨考虑每个数作为答案出现多少次,然后加和
直接做不好做,但是我们发现,当枚举到\(i\) 时,\(a_i\) 成为最终答案的次数仅仅和\(a_1,a_2,\cdots,a_m\) 中哪些比它大,哪些比它小,哪些和它相等有关,而和具体相差多少无关。于是我们可以把其中比它大的看作\(2\), 和它相等的看作\(1\), 比它小的看作\(0\), 然后我们就可以在表达式树上\(dp\)了
记\(f_{u,k}\)表示节点\(u\)的计算结果为\(k\)的方案数,考虑转移
- 当\(u\)是叶子节点时,将对应的状态置为\(1\)即可
- 当\(u\)是非叶子节点时,设其左儿子为\(l\),右儿子为\(r\)
如果\(u\)对应的操作符为\(>\),那么
若其操作符为\(<\),那么
若为\(?\),考虑加法原理,只需把以上两式相加即可
最终答案就是\(f_{rt,1}\)
时间复杂度\(\mathcal O(nm(m+|E|))\)
这样下来复杂度仍然无法承受,考虑优化
能否不枚举\(i\)?答案是肯定的,因为每一次都是\(m\)个数,而每个数都在\(0\)和\(2\)之间,于是我们可以先预处理出所有情况,然后记下答案。每次先将\(a\)数组排序,从小到大地考虑即可
时间复杂度\(\mathcal O(3^m|E|+n(m\log_2m+m))\)
然而预处理的复杂度仍然难以承受,考虑继续优化
可以将小于\(a_i\)的看作\(0\),将大于等于\(a_i\)的看作\(1\), 这样可以求出结果大于等于\(a_i\)的方案数,然后再差分一下就可以得到答案了
时间复杂度\(\mathcal O(2^m|E|+n(m\log_2m+m))\)
可以承受
code
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
const int N=5e4+5,K=12,mod=1e9+7;
int n,m,A[K][N],rt,tot,lb[N],pos[N],sta[N],top;
int ls[N],rs[N],ans,d[K];pii B[K];
char s[N];
inline int read()
{
int s=0,w=1; char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')w=-1;
for(;isdigit(ch);ch=getchar())s=(s<<1)+(s<<3)+(ch^48);
return s*w;
}
void build(int&p,int l,int r)
{
if(pos[r]==l)return build(p,l+1,r-1);
p=++tot;int t=0;
if(l==r){lb[p]=s[l]^48;return;}
for(int i=r;i>=l;--i)
{
if(pos[i]){i=pos[i];continue;}
if(s[i]=='<'||s[i]=='>'||s[i]=='?'){t=i;break;}
}lb[p]=s[t];
build(ls[p],l,t-1),build(rs[p],t+1,r);
}
inline int add(int x,int y){return x+y>=mod?x+y-mod:x+y;}
inline int dec(int x,int y){return x-y<0?x-y+mod:x-y;}
int f[N][2],ret[1200];
inline void upmn(int u)
{
for(int i=0;i<=1;++i)
for(int j=0;j<=1;++j)
{
int&d=f[u][min(i,j)];
d=add(d,1ll*f[ls[u]][i]*f[rs[u]][j]%mod);
}
}
inline void upmx(int u)
{
for(int i=0;i<=1;++i)
for(int j=0;j<=1;++j)
{
int&d=f[u][max(i,j)];
d=add(d,1ll*f[ls[u]][i]*f[rs[u]][j]%mod);
}
}
void dp(int u)
{
f[u][0]=f[u][1]=0;
if(!ls[u]){f[u][d[lb[u]]]=1;return;}
dp(ls[u]),dp(rs[u]);
if(lb[u]!='<')upmx(u);
if(lb[u]!='>')upmn(u);
}
inline int gans(int w)
{
if(ret[w]>=0)return ret[w];
for(int i=0;i<m;++i)d[i]=(w>>i)&1;
dp(rt);return ret[w]=f[rt][1];
}
int main()
{
n=read(),m=read();
for(int i=0;i<m;++i)
for(int j=1;j<=n;++j)
A[i][j]=read();
scanf("%s",s+1);
int len=strlen(s+1);
for(int i=1;i<=len;++i)
{
if(s[i]=='(')sta[++top]=i;
else if(s[i]==')')pos[i]=sta[top--];
}
build(rt,1,len);
int st=1<<m;fill(ret,ret+st,-1);
#define x first
#define y second
for(int i=1;i<=n;++i)
{
for(int j=0;j<m;++j)
B[j]=make_pair(A[j][i],j);
sort(B,B+m);
int p=st-1,pre=gans(p);
for(int j=0;j<m;)
{
int val=B[j].x;
p^=1<<B[j].y,++j;
while(B[j].x==B[j-1].x)p^=1<<B[j].y,++j;
int now=gans(p);
ans=add(ans,1ll*val*dec(pre,now)%mod);
pre=now;
}
}
#undef x
#undef y
printf("%d\n",ans);
return 0;
}
T3
solution
先定义数列\(f\)
然后有结论:数列\(f\)在模\(m\)意义下是纯循环的,且最小正周期是\(\mathcal O(m)\)的(常数也不大)
证明?自己写程序吧
不难证明原题中的\(F\)可以表示为
依题意,即要求最小的\(n\)满足(\(a\)或\(b\)等于\(0\)的情况先特判掉)
即
看上去问题似乎已经解决了,只需预处理所有的\(\frac {f_{n+1}}{f_n}\bmod m\),然后询问时查表即可
然而注意到\(b,f_n\)可能和\(m\)并不互质,这导致其在模\(m\)意义下并不存在逆元。怎么办?
引理:
不妨令\(g=\gcd(a,m-b,m),a'=\frac ag,b'=\frac {m-b}g,m'=\frac mg\),由此
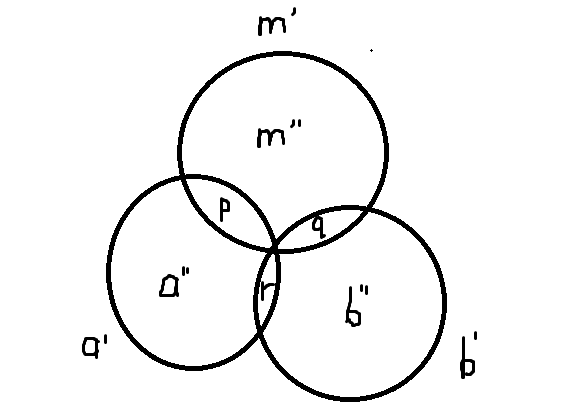
考察如上文氏图
相交的部分代表公共的因子
由于
所以
同理得
由于
(辗转相除求最大公约数的方法可以证明此结论)
因此
而倘若\(m''\mid f_n\),则\(m''\mid f_{n+1}\),与此二者互质矛盾,反之可得相同结论,因此
所以
因此可得
此时的除法显然是有意义的
因此,我们只需采用\(map\) 映射,将四元组\((m',p,q,\frac{\frac{f_{n+1}}p}{\frac{f_n}q}\bmod \frac{m'}{pq})\) 映射到对应的最小的\(n\)即可
预处理时枚举\(m'\) (即\(m\) 的约数),然后花费\(\mathcal O(m')\) 的时间处理出\(m'\) 处的上述四元组
询问时按照上述过程运算,然后查询即可
time complexity
预处理复杂度:\(\mathcal O(\sigma(m)\log_2(\sigma(m)))=\mathcal O(m\ln m(\ln m+\ln\ln m))\) 其中\(\sigma(m)\) 为因数和
查询复杂度:\(\mathcal O(n\log m)\)
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m;
struct node{int p,q,k;};
inline bool operator<(const node&x,const node&y)
{
return x.p!=y.p?x.p<y.p:(x.q!=y.q?x.q<y.q:x.k<y.k);
}
map<node,int>mp[N];
inline int read()
{
int s=0,w=1; char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')w=-1;
for(;isdigit(ch);ch=getchar())s=(s<<1)+(s<<3)+(ch^48);
return s*w;
}
int gcd(int x,int y){return y?gcd(y,x%y):x;}
void exgcd(int&x,int&y,int a,int b)
{
if(!b){x=1,y=0;return;}
exgcd(x,y,b,a%b);
int t=x;x=y,y=t-a/b*y;
}
inline int inv(int a,int mod)
{
int x,y;exgcd(x,y,a,mod);
return (x%mod+mod)%mod;
}
inline void pre()
{
for(int _=2;_<=m;++_)
{
if(m%_)continue;
int x=1,y=0;
for(int cnt=0;;++cnt)
{
if(x&&y)
{
int d1=gcd(_,x),d2=gcd(_,y),pm=_/d1/d2;
int k=1ll*(y/d2)*inv(x/d1,pm)%pm;
if(!mp[_].count({d1,d2,k}))mp[_][{d1,d2,k}]=cnt;
}
int t=x;x=y,y=(y+t)%_;
if(x==1&&y==0)break;
}
}
}
int main()
{
n=read(),m=read();pre();
while(n--)
{
int a=read(),b=read();
if(!a){puts("0");continue;}
if(!b){puts("1");continue;}b=(m-b)%m;
int g=gcd(gcd(a,b),m),m1=m/g;a/=g,b/=g;
int p=gcd(a,m1),q=gcd(b,m1),m2=m1/p/q;
a/=p,b/=q;
int k=1ll*a*inv(b,m2)%m2;
if(!mp[m1].count({q,p,k}))puts("-1");
else printf("%d\n",mp[m1][{q,p,k}]);
}
return 0;
}



