计算几何基础

计算几何基础

UVA11178 Morley's Theorem
此题直接模拟即可，主要是熟悉向量基本运算

#include<bits/stdc++.h>
using namespace std;
typedef double db;
struct vec
{
	db x,y;
	inline void read(){scanf("%lf%lf",&x,&y);}
	inline void print(){printf("%.6lf %.6lf ",x,y);}
};
inline vec operator+(const vec&x,const vec&y){return {x.x+y.x,x.y+y.y};}//向量相加
inline vec operator-(const vec&x,const vec&y){return {x.x-y.x,x.y-y.y};}//向量相减
inline vec operator*(const db&x,const vec&y){return {x*y.x,x*y.y};}//向量数乘
inline db dot(const vec&x,const vec&y){return x.x*y.x+x.y*y.y;}//向量点乘
inline db cross(const vec&x,const vec&y){return x.x*y.y-x.y*y.x;}//向量叉乘
inline db len(const vec&x){return sqrt(x.x*x.x+x.y*x.y);}//向量模长
inline db ang(const vec&x,const vec&y){return acos(dot(x,y)/len(x)/len(y));}//向量夹角：dot(a,b)=|a||b|cos<a,b>
inline vec inr(const vec&P,const vec&v,const vec&Q,const vec&w)
{
	vec u=P-Q;
	double t1=cross(w,u)/cross(v,w);
	return P+t1*v;
}////直线焦点
inline vec rot(const vec&x,db rad)
{
	return {x.x*cos(rad)-x.y*sin(rad),x.x*sin(rad)+x.y*cos(rad)};
}//向量逆时针旋转rad
inline vec solve(const vec&A,const vec&B,const vec&C)
{
	vec v1=C-B;
	double a=ang(A-B,v1);
	v1=rot(v1,a/3);
	vec v2=B-C;
	double b=ang(A-C,v2);
	v2=rot(v2,-b/3);
	return inr(B,v1,C,v2);
}
vec A,B,C,D,E,F;
int main()
{
	int T;scanf("%d",&T);
	while(T--)
	{
		A.read(),B.read(),C.read();
		D=solve(A,B,C);
		E=solve(B,C,A);
		F=solve(C,A,B);
		D.print(),E.print(),F.print();puts("");
	}
	return 0;
}

UVA1342 That Nice Euler Circuit
求一个多边形把平面分成了多少个部分
此题主要是欧拉定理

\[V+F-E=2 \]

因此求出顶点个数和边数即可
顶点个数可以线段两两求交后去重
边数可以每发现一个点在边上就把边数加一，原因是它会把当前边新分割出一部分

#include<bits/stdc++.h>
using namespace std;
typedef double db;
const int N=305;
const db eps=1e-7;
inline int sig(const db&x){return fabs(x)<eps?0:(x<0?-1:1);}
struct vec
{
	db x,y;
	inline void read(){scanf("%lf%lf",&x,&y);}
	inline void print(){printf("%.6lf %.6lf ",x,y);}
}p[N],v[N*N];
inline bool operator<(const vec&x,const vec&y){return x.x<y.x||(x.x==y.x&&x.y<y.y);}
inline bool operator==(const vec&x,const vec&y){return sig(x.x-y.x)==0&&sig(x.y-y.y)==0;}
inline vec operator+(const vec&x,const vec&y){return {x.x+y.x,x.y+y.y};}
inline vec operator-(const vec&x,const vec&y){return {x.x-y.x,x.y-y.y};}
inline vec operator*(const db&x,const vec&y){return {x*y.x,x*y.y};}
inline db dot(const vec&x,const vec&y){return x.x*y.x+x.y*y.y;}
inline db cross(const vec&x,const vec&y){return x.x*y.y-x.y*y.x;}
inline vec inr(const vec&P,const vec&v,const vec&Q,const vec&w)
{
	vec u=P-Q;
	double t1=cross(w,u)/cross(v,w);
	return P+t1*v;
}
inline bool pd(const vec&a1,const vec&a2,const vec&b1,const vec&b2)
{
	db c1,c2,c3,c4;
	c1=cross(a2-a1,b1-a1),c2=cross(a2-a1,b2-a1);
	c3=cross(b2-b1,a1-b1),c4=cross(b2-b1,a2-b1);
	return sig(c1)*sig(c2)<0&&sig(c3)*sig(c4)<0;
}//判断两线段是否规范相交：每一条线段的两个端点都在另一条线段的两侧
inline bool ons(const vec&p,const vec&a,const vec&b)
{
	return sig(cross(a-p,b-p))==0&&sig(dot(a-p,b-p))<0;
}//判断点是否在线段上：叉积为0且和线段两端连线的夹角是钝角（准确来说应该是平角）
int main()
{
	int kase=0,n;
	while(scanf("%d",&n)==1&&n)
	{
		for(int i=1;i<=n;++i)p[i].read(),v[i]=p[i];
		int c=n-1,e=n-1;
		for(int i=1;i<n;++i)
			for(int j=i+1;j<n;++j)
				if(pd(p[i],p[i+1],p[j],p[j+1]))
					v[++c]=inr(p[i],p[i+1]-p[i],p[j],p[j+1]-p[j]);
		sort(v+1,v+c+1);
		int tot=unique(v+1,v+c+1)-v-1;
		for(int i=1;i<=tot;++i)
			for(int j=1;j<n;++j)
				if(ons(v[i],p[j],p[j+1]))++e;
		printf("Case %d: There are %d pieces.\n",++kase,e+2-tot);
	}
	return 0;
}

UVA12304 2D Geometry 110 in 1!
任务一：求三角形外接圆
中垂线求交点
任务二：求三角形内切圆
角平分线求交点
任务三：过已知点求已知圆的切线
可以通过点到圆心的距离判断解的个数

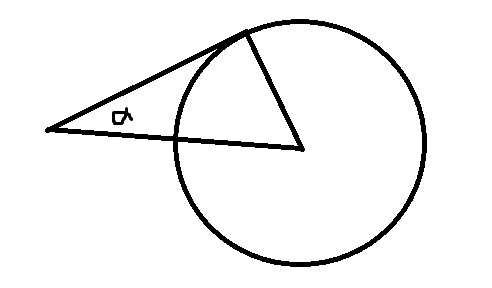
容易求出\(\alpha\)，那么旋转一下就可以求出切线极角了
任务四：求所有点满足到定直线距离为\(r\)且到定点距离为\(r\)，其中\(r\)给定
将定直线延其垂直方向平移\(r\)可得两条直线
这两条直线和以定点为圆心，\(r\)为半径的圆求交点即可
任务五：求到两定直线距离为\(r\)的点，其中\(r\)给定
和任务四类似得到四条直线两两求交
任务六：求所有半径为\(r\)且和两给定圆外切的圆的圆心
将原先的两个圆的半径增加\(r\)，然后再求交点即可得到答案

#include<bits/stdc++.h>
using namespace std;
typedef double db;
const db eps=1e-8,pi=acos(-1.0);
inline int sig(const db&x){return fabs(x)<eps?0:(x<0?-1:1);}
struct vec
{
	db x,y;
	vec(db _x=0.0,db _y=0.0){x=_x,y=_y;}
	inline void read(){scanf("%lf%lf",&x,&y);}
	inline void print()const{printf("(%.6lf,%.6lf)",x,y);}
	inline bool operator==(const vec&rhs)const{return sig(x-rhs.x)==0&&sig(y-rhs.y)==0;}
	inline bool operator<(const vec&rhs)const{return sig(x-rhs.x)==0?sig(y-rhs.y)<0:sig(x-rhs.x)<0;}
	inline vec operator+(const vec&rhs)const{return vec(x+rhs.x,y+rhs.y);}
	inline vec operator-(const vec&rhs)const{return vec(x-rhs.x,y-rhs.y);}
	inline vec operator*(const db&p)const{return vec(p*x,p*y);}
	inline vec operator/(const db&p)const{return vec(x/p,y/p);}
	inline db len()const{return sqrt(x*x+y*y);}
	inline db ang()const{return atan2(y,x);}//向量极角
};
typedef vector<vec> vv;
inline db dot(const vec&x,const vec&y){return x.x*y.x+x.y*y.y;}
inline db cross(const vec&x,const vec&y){return x.x*y.y-x.y*y.x;}
inline vec rot(const vec&p,const db&rad){return vec(p.x*cos(rad)-p.y*sin(rad),p.x*sin(rad)+p.y*cos(rad));}
inline vec rot90(const vec&p){return vec(-p.y,p.x);}//求向量法向量
inline db ang(const vec&p,const vec&q){return acos(dot(p,q)/(p.len())/(q.len()));}
inline db todg(const db&x)
{
	db ans=x/pi*180;
	while(sig(ans)<0)ans+=180;
	while(sig(180-ans)<0)ans-=180;
	return ans;
}//弧度转度数
struct cir
{
	vec o;db r;
	inline void read(){o.read();scanf("%lf",&r);}
	inline db ang(const vec&p)const{return atan2(p.y-o.y,p.x-o.x);}
	inline vec pt(const db&rad)const{return vec(o.x+r*cos(rad),o.y+r*sin(rad));}//已知圆心角求点
};
inline db dis(const vec&P,const vec&Q){return (P-Q).len();}
inline db dis(const vec&P,const vec&v,const vec&Q)
{
	return fabs(cross(Q-P,v)/v.len());
}//点到直线距离
inline vec pro(const vec&P,const vec&v,const vec&Q)
{
	db t=dot(Q-P,v)/v.len();
	return P+v/v.len()*t;
}//点在直线上的投影
inline vec inr(const vec&P,const vec&v,const vec&Q,const vec&w)
{
	vec u=P-Q;
	db t=cross(u,w)/cross(w,v);
	return P+v*t;
}
inline int inr(const cir&c,const vec&P,const vec&v,vv&sol)
{
	db d=dis(P,v,c.o);
	if(sig(d-c.r)>0)return 0;
	else if(sig(d-c.r)==0)
	{
		sol.push_back(pro(P,v,c.o));
		return 1;
	}
	vec mid=pro(P,v,c.o),e=v/v.len();
	db l=sqrt(c.r*c.r-d*d);
	sol.push_back(mid+e*l);
	sol.push_back(mid-e*l);
	return 2;
}//圆和直线的交点：主要考虑垂径三角形
inline int inr(const cir&a,const cir&b,vv&sol)
{
	db d=dis(a.o,b.o);
	if(sig(d-a.r-b.r)>0)return 0;
	else if(sig(d-a.r-b.r)==0)
	{
		sol.push_back(a.pt(a.ang(b.o)));
		return 1;
	}
	db ag=a.ang(b.o),dl=acos((a.r*a.r+d*d-b.r*b.r)/(2*a.r*d));
	sol.push_back(a.pt(ag+dl));
	sol.push_back(a.pt(ag-dl));
	return 2;
}//圆和圆的交点
inline int gtg(const cir&a,const vec&P,vector<db>&sol)
{
	db d=dis(a.o,P);
	if(sig(a.r-d)>0)return 0;
	else if(sig(a.r-d==0))
	{
		sol.push_back(todg(rot90(P-a.o).ang()));
		return 1;
	}
	db dl=asin(a.r/d),ag=(a.o-P).ang();
	sol.push_back(todg(ag-dl));
	sol.push_back(todg(ag+dl));
	return 2;
}//求切线
inline void print(vv&ans)
{
	putchar('[');
	sort(ans.begin(),ans.end());int tot=ans.size();
	for(int i=0;i<tot;++i)ans[i].print(),printf(i==tot-1?"":",");
	putchar(']');puts("");
}
inline void print(vector<db>&ans)
{
	putchar('[');
	sort(ans.begin(),ans.end());int tot=ans.size();
	for(int i=0;i<tot;++i)printf("%.6lf",ans[i]),printf(i==tot-1?"":",");
	putchar(']');puts("");
}
char ch[200];
inline void solve1()
{
	vec A,B,C;A.read(),B.read(),C.read();
	vec ans=inr((A+B)/2,rot90(B-A),(B+C)/2,rot90(B-C));
	printf("(%.6lf,%.6lf,%.6lf)\n",ans.x,ans.y,dis(ans,A));
}
inline void solve2()
{
	vec A,B,C;A.read(),B.read(),C.read();
	vec c=B-A,b=C-A,a=C-B;
	c=c/c.len(),a=a/a.len(),b=b/b.len();
	vec ans=inr(A,b+c,C,a+b);
	printf("(%.6lf,%.6lf,%.6lf)\n",ans.x,ans.y,dis(A,B-A,ans));
}
inline void solve3()
{
	vector<db>sol;
	cir c;vec t;c.read(),t.read();
	gtg(c,t,sol);print(sol);
}
inline void solve4()
{
	vec P,A,B;db r;P.read(),A.read(),B.read();scanf("%lf",&r);
	vec e=rot90(B-A)/dis(B,A);
	vec C=A+e*r,D=A-e*r;vv sol;
	cir c;c.o=P,c.r=r;
	inr(c,C,B-A,sol);inr(c,D,B-A,sol);
	print(sol);
}
inline void solve5()
{
	vec A,B,C,D;db r;
	A.read(),B.read(),C.read(),D.read();scanf("%lf",&r);
	vec e1=rot90(B-A)/dis(B,A),e2=rot90(D-C)/dis(D,C);
	vec A1=A+e1*r,A2=A-e1*r,C1=C+e2*r,C2=C-e2*r;vv sol;
	sol.push_back(inr(A1,B-A,C1,D-C));
	sol.push_back(inr(A2,B-A,C1,D-C));
	sol.push_back(inr(A1,B-A,C2,D-C));
	sol.push_back(inr(A2,B-A,C2,D-C));print(sol);
}
inline void solve6()
{
	cir a,b;db r;a.read(),b.read();scanf("%lf",&r);
	a.r+=r,b.r+=r;vv sol;
	inr(a,b,sol);print(sol);
}
int main()
{
	while(scanf("%s",ch)!=EOF)
	{
		if(ch[0]=='I')solve2();
		else if(ch[0]=='T')solve3();
		else if(ch[4]=='u')solve1();
		else if(ch[7]=='h')solve4();
		else if(ch[18]=='L')solve5();
		else solve6();
	}
	return 0;
}

UVA1308 Viva Confetti
一些圆盘被依次放在平面上，询问有多少个圆盘是可见的
sol.
容易发现每一个可视的部分都是由若干个小圆弧围成的
求出小圆弧可以通过两两枚举圆求交
特别地，如果某个圆和其他圆没有交点，那么这个圆就是一个圆弧
求得小圆弧后，将其中点向内和向外都移动一极小距离，然后标记新位置的最顶上的圆弧是可见的
为什么？见下图：

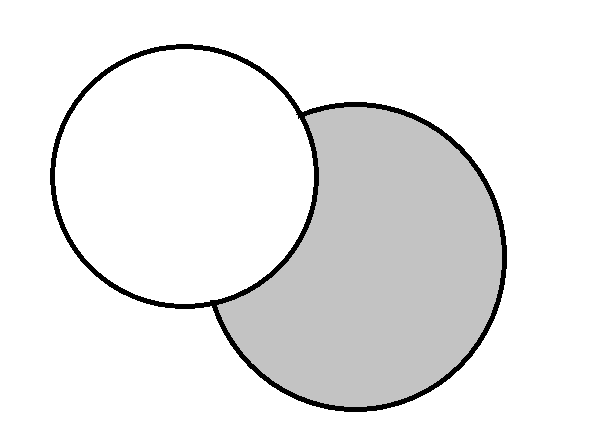
显然，在不和白色圆相交的前提下（否则灰色圆就不是最顶了，况且这还和白色圆产生了新圆弧）
是不可能通过圆这种凸的图形将灰色圆剩余部分这种凹的图形完美地覆盖的

UVA10652 Board Wrapping
直接上凸包就可以了
考虑\(Andrew\)算法，将所有点按照\(x\)从小到大排序，若相同则按照\(y\)从小到大排序
从前往后扫，同时用栈记下当前在凸包中的点，如果新加入的点和之前的点形成凹进去的图形则弹栈（可以用叉积正负判断（右手定则））
这样可以求出下凸壳
同理求出上凸壳

#include<bits/stdc++.h>
using namespace std;
typedef double db;
const int N=2505;
const db eps=1e-7,pi=acos(-1.0);
inline int sig(const db&x){return fabs(x)<eps?0:(x<0?-1:1);}
struct vec{db x,y;}p[N],q[N];
inline bool operator<(const vec&x,const vec&y){return x.x<y.x||(x.x==y.x&&x.y<y.y);}
inline bool operator==(const vec&x,const vec&y){return sig(x.x-y.x)==0&&sig(x.y-y.y)==0;}
inline vec operator+(const vec&x,const vec&y){return {x.x+y.x,x.y+y.y};}
inline vec operator-(const vec&x,const vec&y){return {x.x-y.x,x.y-y.y};}
inline db cross(const vec&x,const vec&y){return x.x*y.y-x.y*y.x;}
inline db torad(const db&x){return x/180*pi;} 
inline vec rot(const vec&x,db rad)
{
	return {x.x*cos(rad)-x.y*sin(rad),x.x*sin(rad)+x.y*cos(rad)};
}
inline int Andrew(int n)
{
	sort(p+1,p+n+1);int m=0;
	for(int i=1;i<=n;++i)
	{
		while(m>1&&sig(cross(q[m]-q[m-1],p[i]-q[m-1]))<=0)--m;
		q[++m]=p[i];
	}
	int k=m;
	for(int i=n-1;i;--i)
	{
		while(m>k&&sig(cross(q[m]-q[m-1],p[i]-q[m-1]))<=0)--m;
		q[++m]=p[i];
	}
	m-=n>1;return m;
}
inline db S(int n)
{
	db ans=0.0;
	for(int i=2;i<n;++i)
		ans+=cross(q[i]-q[1],q[i+1]-q[1]);
	ans/=2;
	return fabs(ans);
}//三角剖分求多边形面积
int main()
{
	int T;scanf("%d",&T);
	while(T--)
	{
		int n,tot=0;scanf("%d",&n);
		db S1=0.0,S2=0.0;
		for(int i=1;i<=n;++i)
		{
			db x,y,w,h,j;
			scanf("%lf%lf%lf%lf%lf",&x,&y,&w,&h,&j);
			j=-torad(j);vec o={x,y};
			p[++tot]=o+rot({w/2,h/2},j);
			p[++tot]=o+rot({w/2,-h/2},j);
			p[++tot]=o+rot({-w/2,h/2},j);
			p[++tot]=o+rot({-w/2,-h/2},j);
			S1+=w*h;
		}
		S2=S(Andrew(tot));
		printf("%.1lf %%\n",S1*100/S2);
	}
	return 0;
}

UVA11168 Airport
给出平面上\(n\)个点，找一条直线，要求所有点在直线的同侧（也可以在直线上），使得到直线的距离之和尽量小
sol.
比较显然的是这条直线一定是凸包上某条边所在直线，于是先求出凸包
现在的问题变为了如何快速求得所有点到当前枚举到的直线的距离之和
联系到解析几何中的点到直线距离公式（\((x_0,y_0)\)到直线\(Ax+By+C=0\)的距离）

\[d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}} \]

同时由于所有点都在直线的同一侧，因此绝对值内的东西的符号都是相同的，可以直接加起来
只需要记下所有点的横坐标之和和纵坐标之和就可以快速查询了
另外还有一个小细节：已知两点如何求过这两点的直线方程
已知\((x_1,y_1),(x_2,y_2)\)不难得到直线方程:

\[(y_1-y_2)x+(x_2-x_1)y+x_1y_2-y_1x_2=0 \]

时间复杂度:\(\mathcal O(nlog_2n)\)

#include<bits/stdc++.h>
using namespace std;
typedef double db;
const db eps=1e-7;
const int N=1e4+5;
inline int sig(db x){return x>eps?1:(x<-eps?-1:0);}
struct vec{db x,y;}p[N];
inline bool operator<(const vec&x,const vec&y){return x.x<y.x||(x.x==y.x&&x.y<y.y);}
inline bool operator==(const vec&x,const vec&y){return sig(x.x-y.x)==0&&sig(x.y-y.y)==0;}
inline vec operator-(const vec&x,const vec&y){return vec{x.x-y.x,x.y-y.y};}
inline db cross(const vec&x,const vec&y){return x.x*y.y-x.y*y.x;}
int n,q[N];
inline int Andrew()
{
	sort(p+1,p+n+1);int m=0;
	for(int i=1;i<=n;++i)
	{
		while(m>1&&sig(cross(p[q[m]]-p[i],p[q[m-1]]-p[i]))>=0)--m;
		q[++m]=i;
	}
	int k=m;
	for(int i=n;i>=1;--i)
	{
		while(m>k&&sig(cross(p[q[m]]-p[i],p[q[m-1]]-p[i]))>=0)--m;
		q[++m]=i;
	}
	m-=n>1;return m;
}
int main()
{
	int T;scanf("%d",&T);
	for(int kase=1;kase<=T;++kase)
	{
		scanf("%d",&n);db sx=0,sy=0;
		for(int i=1;i<=n;++i)
			scanf("%lf%lf",&p[i].x,&p[i].y),sx+=p[i].x,sy+=p[i].y;
		if(n<=2){printf("Case #%d: 0.000\n",kase);continue;}
		int num=Andrew();db ans=1e18;
		for(int i=1;i<=num;++i)
		{
			int j=i==num?1:i+1;
			db xa=p[q[i]].x,xb=p[q[j]].x;
			db ya=p[q[i]].y,yb=p[q[j]].y;
			db A=ya-yb,B=xb-xa,C=xa*yb-ya*xb;
			ans=min(ans,fabs(A*sx+B*sy+C*n)/sqrt(A*A+B*B));
		}
		printf("Case #%d: %.3lf\n",kase,ans/n);
	}
	return 0;
}

UVA10256 The Great Divide
平面上给定\(n\)个红点和\(m\)个蓝点，询问是否存在一条直线使得对于任意一对红点和蓝点，他们都位于直线两侧
sol.
不难发现原问题等价于红点组成的凸包和蓝点组成的凸包是相离的
如何判断两个凸包是否相离呢？
首先，任取红凸包上一点边和蓝凸包上一边都是不相交的
其次，红凸包的任意一个顶点不在蓝凸包内部，蓝凸包的任意一个顶点不在红凸包内部
线段相交有之前的模板
点是否在凸包内可以二分（不过由于本题数据不大，没有必要）
也可以采用一种类似于转角的方法（利用叉积，具体详见代码）
时间复杂度\(\mathcal O(nm)\)

#include<bits/stdc++.h>
using namespace std;
typedef double db;
const db eps=1e-7;
const int N=1e3+5;
inline int sig(db x){return x>eps?1:(x<-eps?-1:0);}
struct vec{db x,y;};
inline bool operator<(const vec&x,const vec&y){return x.x<y.x||(x.x==y.x&&x.y<y.y);}
inline bool operator==(const vec&x,const vec&y){return sig(x.x-y.x)==0&&sig(x.y-y.y)==0;}
inline vec operator-(const vec&x,const vec&y){return vec{x.x-y.x,x.y-y.y};}
inline db cross(const vec&x,const vec&y){return x.x*y.y-x.y*y.x;}
inline db dot(const vec&x,const vec&y){return x.x*y.x+x.y*y.y;}
inline bool onseg(const vec&A,const vec&B,const vec&p)
{
	return A==p||B==p||(sig(cross(A-p,B-p))==0&&sig(dot(A-p,B-p))<0);
}
inline bool inr(const vec&A,const vec&B,const vec&C,const vec&D)
{
	db a=cross(C-D,A-D),b=cross(C-D,B-D);
	db c=cross(A-B,D-B),d=cross(A-B,C-B);
	return sig(a)*sig(b)<=0&&sig(c)*sig(d)<=0;
}
struct poly
{
	vec p[N],np[N];int q[N],m,n;
	inline void read()
	{
		for(int i=1;i<=n;++i)
			scanf("%lf%lf",&p[i].x,&p[i].y);
	}
	inline void Andrew()
	{
		sort(p+1,p+n+1);m=0;
		for(int i=1;i<=n;++i)
		{
			while(m>1&&sig(cross(p[q[m]]-p[i],p[q[m-1]]-p[i]))>=0)--m;
			q[++m]=i;
		}
		int k=m;
		for(int i=n;i>=1;--i)
		{
			while(m>k&&sig(cross(p[q[m]]-p[i],p[q[m-1]]-p[i]))>=0)--m;
			q[++m]=i;
		}m-=n>1;
		for(int i=1;i<=m;++i)np[i]=p[q[i]];
	}
	inline bool in(const vec&p)
	{
		if(m==1)return np[1]==p;
		if(m==2)return onseg(np[1],np[2],p);
		for(int i=1;i<=m;++i)
		{
			int j=i==m?1:i+1;
			if(onseg(np[i],np[j],p))return true;
			if(sig(cross(np[i]-p,np[j]-p))<0)return false;
		}return true;
	}
}A,B;
int n,m;
int main()
{
	while(1)
	{
		scanf("%d%d",&n,&m);if(!n&&!m)break;
		A.n=n,B.n=m;A.read(),B.read();
		A.Andrew();B.Andrew();bool flag=0;
		for(int a=1;a<=A.m&&!flag;++a)
		{
			int b=a==A.m?1:a+1;
			for(int c=1;c<=B.m&&!flag;++c)
			{
				int d=c==B.m?1:c+1;
				if(inr(A.np[a],A.np[b],B.np[c],B.np[d]))flag=1;
			}
		}if(flag){puts("No");continue;}
		for(int i=1;i<=A.m&&!flag;++i)
			if(B.in(A.np[i]))flag=1;
		for(int i=1;i<=B.m&&!flag;++i)if(A.in(B.np[i]))flag=1;
		puts(flag?"No":"Yes");
	}
	return 0;
}