多项式全家桶
快速傅里叶变换
多项式的系数表示法
\[f(x)=\sum_{i=0}^{n-1}a_ix^i
\]
即
\[f(x)\rightarrow \{a_0,a_1,a_2\dots ,a_{n-1}\}
\]
多项式的点值表示法
注意到一个最高次数为\(n-1\)的多项式可以由\(n\)个点值唯一确定
即将互不相同的\(\{x_0,x_1,\dots ,x_{n-1}\}\)带入\(f(x)\)得到\(n\)个取值\(\{f(x_0),f(x_1),\dots ,f(x_{n-1})\}\)
因此
\[f(x)\rightarrow \{f(x_0),f(x_1),\dots ,f(x_{n-1})\}
\]
多项式乘法
注意到如果用系数表示法，直接做的复杂度为\(\mathcal O(n^2)\)（类似于高精度乘法）
但如果是点值表示法则可以做到\(\mathcal O(n)\)
即，对于两个多项式
\[f(x)\rightarrow \{f(x_0),f(x_1),\dots ,f(x_{n-1})\}\\
g(x)\rightarrow \{g(x_0),g(x_1),\dots ,g(x_{n-1})\}
\]
那么
\[h(x)=f(x)g(x)\rightarrow \{f(x_0)g(x_0),f(x_1)g(x_1),\dots ,f(x_{n-1})g(x_{n-1})\}
\]
然而虽然理想美好，但是现实却很残酷
一般情况下都是用的系数表示法
于是自然而然地想到将系数表示法转化为点值表示法，乘出来之后再变回来
显然，暴力得到点值仍然是\(\mathcal O(n^2)\)的
于是我们考虑一些特殊的值带入
复数中的单位根
注意以下的\(n\)都是\(2\)的整数次幂
对于方程
\[x^n=1
\]
由代数基本定理，这个方程应该存在\(n\)个根
不妨设这\(n\)个根为\(w_n^0,w_n^1,\dots ,w_n^{n-1}\)
容易发现
\[w_n^k=cos(\frac{2\pi}nk)+i\cdot sin(\frac{2\pi}nk)
\]
可以结合复平面上的单位圆进行理解
然后单位根有如下神奇性质
\[w_n^a=w_{2n}^{2a}\\
w_n^a=-w_n^{a+\frac n2}\\
w_n^a=w_n^{a-n}
\]
然后就可以开始搞事情了
进入正题
注意以下的\(n\)都是\(2\)的整数次幂
不妨设
\[f(x)=a_0+a_1x+a_2x^2\dots +a_{n-1}x^{n-1}\\
A(x)=a_0+a_2x+a_4x^2\dots +a_{n-2}x^{\frac{n-2}2}\\
B(x)=a_1+a_3x+a_5x^2\dots +a_{n-1}x^{\frac{n-2}2}
\]
即按照奇偶性分类
那么我们有
\[f(x)=A(x^2)+x\cdot B(x^2)
\]
然后可以注意到
\[f(w_n^k)=A(w_n^{2k})+w_n^k\cdot B(w_n^{2k})\\
=A(w_{\frac n2}^k)+w_n^k\cdot B(w_{\frac n2}^k)
\]
而
\[f(w_n^{k+\frac n2})=A(w_n^{2k+n})+w_n^{k+\frac n2}\cdot B(w_n^{2k+n})\\
=A(w_n^{2k})+w_n^{k+\frac n2}\cdot B(w_n^{2k})\\
=A(w_{\frac n2}^k)-w_n^k\cdot B(w_{\frac n2}^k)
\]
于是我们在计算\(f(w_n^k)\)时就可以顺便计算出\(f(w_n^{k+\frac n2})\)的值
这样就可以把\(\mathcal O(n^2)\)优化到\(\mathcal O(n\log_2n)\)
现在的问题就在于如何把点值再变回系数
考虑我们现在已经求出\(h(x)=f(x)*g(x)\)在\(w_n^0,w_n^1,\dots w_n^{n-1}\)处的点值，需要求出\(h(x)\)的各项系数\(b_i\)
考虑如此构造函数
\[C(x)=\sum_{i=0}^{n-1}h(w_n^i)x^i
\]
那么
\[C(x)=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}b_j(w_n^i)^jx^i
\]
考虑将\(x=w_n^{-0},w_n^{-1},\dots w_n^{-(n-1)}\)带入\(C(x)\)
\[C(w_n^{-k})=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}b_j(w_n^i)^j(w_n^{-k})^i\\
=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}b_j(w_n^{j-k})^i\\
=\sum_{j=0}^{n-1}b_j\sum_{i=0}^{n-1}(w_n^{j-k})^i
\]
考虑单位根反演定理
\[[n|k]=\frac 1n\sum_{i=0}^{n-1}(w_n^k)^i
\]
考虑证明此结论
当\(n\mid k\)时，显然\(w_n^k=1\),因此原式\(=\frac 1n\sum_{i=0}^{n-1}1^i=1\)
当\(n\nmid k\)时，原式\(=\frac 1n\cdot \frac{(w_n^k)^n-1}{w_n^k-1}=\frac 1n\cdot \frac{w_n^{kn}-1}{w_n^k-1}=\frac 1n\cdot \frac{1-1}{w_n^k-1}=0\)
因此
\[C(w_n^{-k})=\sum_{j=0}^{n-1}b_jn[n\mid j-k]=nb_k
\]
所以我们只用求出\(C(x)\)在\(x=w_n^{-0},w_n^{-1},\dots w_n^{-(n-1)}\)的所有点值，最后再\(/n\)，就可以计算出\(h(x)\)的各项系数了
于是我们就在\(\mathcal O(n\log_2n)\)的时间内完成了多项式乘法
但是倘若直接按照这样递归模拟，常数极大
我们考虑进行优化，直接把每个数交换到对应的位置上
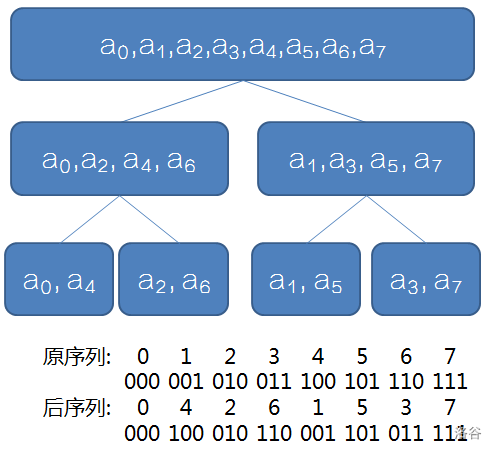
可以发现：交换后序列的位置为 交换前序列的二进制下 翻转过来
可以通过如下代码进行实现
for(int i=0;i<lim;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
在函数中这样实现
for(int i=0;i<lim;++i)if(i<rev[i])swap(f[i],f[rev[i]]);
这样就可以化递归为迭代，大大减小常数
还有其他优化：比如预处理单位根。比较trivial就不再赘述了
完整代码
inline void fft(pt*p,int lim,int tp)
{
for(int i=0;i<lim;++i)if(i<rev[i])swap(p[i],p[rev[i]]);
for(int mid=1;mid<lim;mid<<=1)
{
pt w=pt(1.0,0.0),wn=pt(cos(pi/mid),1.0*tp*sin(pi/mid));
for(int len=mid<<1,j=0;j<lim;j+=len,w=pt(1.0,0.0))
for(int k=0;k<mid;++k,w=w*wn)
{
pt x=p[j+k],y=w*p[j+mid+k];
p[j+k]=x+y,p[j+mid+k]=x-y;
}
}
}
其中\(tp=1\)表示为快速傅里叶变换，\(tp=-1\)表示快速傅里叶逆变换
快速数论变换
存在意义
普通的\(FFT\)显然无法支持取模操作
同时由于运用浮点数进行运算，包括大量使用如\(\sin,\cos\)这些函数，精度难免有误差
于是快速数论变换应运而生
阶
若 \(a,p\)互素，且 \(p>1\)，
对于 \(a^n≡1(mod\ p)\)最小的 \(n\)，我们称之为 \(a\)模 \(p\)的阶,记做 \(δ_p(a)\)
例如： \(δ_7(2)=3\)
原根
设 \(p\)是正整数，\(a\)是整数，若 \(δ_p(a)\)等于\(\varphi (p)\)，则称 \(a\)为模 \(p\)的一个原根，记为 \(g\)
\(δ_7(3)=6=\varphi (7)\)，因此\(3\)模\(7\)的一个原根
注意原根的个数是不唯一的
原根有一个极其重要的性质
若\(P\)为素数，假设一个数\(g\)是\(P\)的原根，那么\(g^i \pmod P (0<i<P)\)的结果两两不同
进入正题
下证
\[w_n^k\equiv(g^{\frac {p-1}n})^k\pmod p
\]
考虑单位根的所有性质
-
\(w_n^k=w_{2n}^{2k}\)
\(\Leftrightarrow (g^{\frac {p-1}n})^k\equiv (g^{\frac {p-1}{2n}})^{2k}\pmod p\)显然成立
-
\(w_n^k=-w_n^{k+\frac n2}\)
\(\Leftrightarrow (g^{\frac {p-1}n})^k\equiv -(g^{\frac {p-1}n})^{k+\frac n2}\)
\(\Leftrightarrow g^{\frac {p-1}{2}}\equiv -1\)
-
\(w_n^k=w_n^{k-n}\)
\(\Leftrightarrow (g^{\frac {p-1}n})^k\equiv (g^{\frac {p-1}n})^{k-n}\)
\(\Leftrightarrow g^{p-1}\equiv 1\)
因此我们就可以用原根来替换单位根
常用的模数有\(998244353,1004535809,469762049\)，它们的原根都是\(3\)
其他地方都和\(FFT\)一模一样
代码如下
inline void ntt(int lim,poly&f,bool tp)
{
for(int i=0;i<lim;++i)if(i<rev[i])swap(f[i],f[rev[i]]);
for(int mid=1;mid<lim;mid<<=1)
{
int sw=qpow(tp?ivG:G,(mod-1)/(mid<<1));
wn[0]=1;for(int i=1;i<mid;++i)wn[i]=mll(wn[i-1],sw);
for(int len=mid<<1,p=0;p+len-1<lim;p+=len)
for(int k=0;k<mid;++k)
{
int x=f[p+k],y=1ll*wn[k]*f[p+mid+k]%mod;
f[p+k]=add(x,y),f[p+mid+k]=dec(x,y);
}
}
}
多项式求逆
给出\(n-1\)次函数\(f(x)\)，求函数\(g(x)\)满足
\[g(x)\equiv\frac 1{f(x)}\pmod {x^n}
\]
系数均对\(998244353\)取模
考虑倍增法
不妨设我们已经求得函数\(g_0\)满足
\[g_0\cdot f\equiv 1\pmod {x^{\frac n2}}
\]
又由于
\[g\cdot f\equiv 1\pmod {x^{\frac n2}}
\]
所以
\[f\cdot (g-g_0)\equiv 0\pmod {x^{\frac n2}}\\
g-g_0\equiv 0\pmod {x^{\frac n2}}\\
(g-g_0)^2\equiv 0\pmod {x^{n}}\\
g^2-2g\cdot g_0+g_0^2\equiv 0\pmod {x^{n}}\\
f\cdot (g^2-2g\cdot g_0+g_0^2)\equiv 0\pmod {x^{n}}\\
g-2g_0+f\cdot g_0^2\equiv 0\pmod {x^{n}}\\
g\equiv 2g_0-f\cdot g_0^2\pmod {x^{n}}\\
\]
特别地，当\(f(x)=c\)时，\(g(x)=c^{p-1}\)
然后递归求解即可
注意此处常数的优化
poly ginv(int n,poly f)
{
if(n==1){poly g;g[0]=qpow(f[0],mod-2);return g;}
poly g=ginv(n+1>>1,f),h,p=g;
int lim=1,l=0;while(lim<n+n)lim<<=1,++l;
for(int i=0;i<lim;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
f.pre(n,lim),p.pre(n,lim);
ntt(lim,f,0),ntt(lim,p,0);
for(int i=0;i<lim;++i)f[i]=mll(f[i],mll(p[i],p[i]));
ntt(lim,f,1);int iv=qpow(lim,mod-2);
for(int i=0;i<n;++i)h[i]=dec(add(g[i],g[i]),mll(f[i],iv));
return h;
}
多项式\(\text{ln}\)
给出\(n-1\)次的多项式函数\(f(x)\),求函数\(g(x)\)满足
\[g(x)\equiv\ln f(x)\pmod {x^n}
\]
系数均对\(998244353\)取模,保证\(f(0)=1\)
两边同时求导可以得到
\[g'\equiv(\ln f)'\pmod {x^n}\\
g'\equiv\frac {f'}f\pmod {x^n}\\
g\equiv \int \frac {f'}f\pmod {x^n}
\]
于是多项式求逆+多项式求导+多项式积分即可
来康康具体实现
inline void igl(int n,poly&f)
{
for(int i=n-1;i;--i)f[i]=mll(f[i-1],inv[i]);f[0]=0;
}//积分
inline void diff(int n,poly&f)
{
for(int i=0,t=f[i+1];i<n-1;++i,t=f[i+1])f[i]=mll(t,i+1);f[n-1]=0;
}//微分
inline poly ln(int n,poly f)
{
poly g=ginv(n,f),h;diff(n,f);
h=mul(n,n,g,f);igl(n,h);
return h;
}
多项式牛顿迭代
对于函数方程
\[F(G(x))\equiv 0\pmod {x^n}
\]
已知\(F(x)\)，求\(G(x)\)
类似于倍增法
假设我们已经求出\(G_0(x)\)满足
\[F(G_0(x))\equiv 0\pmod {x^{\frac n2}}
\]
考虑在\(G_0(x)\)处使用泰勒展开
\[F(G(x))=\sum_{i=0}^{+\infty}\frac{F^{(i)}(G_0(x))}{i!}(G(x)-G_0(x))^i
\]
其中\(f^{(i)}\)表示对\(f\)求\(i\)阶导
注意这个地方是把\(G(x)\)当做自变量,\(G_0(x)\)当作常数，因此不用考虑链式法则等因素
容易知道
\[G(x)-G_0(x)\equiv 0\pmod {x^{\frac n2}}
\]
因此对于\(\forall i\ge2\)
\[(G(x)-G_0(x))^i\equiv 0\pmod {x^n}
\]
所以
\[F(G(x))\equiv F(G_0(x))+F'(G_0(x))(G(x)-G_0(x))\pmod {x^n}\\
\Leftrightarrow F(G_0(x))+F'(G_0(x))G(x)-F'(G_0(x))G_0(x)\equiv 0\pmod {x^n}\\
\Leftrightarrow G(x)\equiv G_0(x)-\frac{F(G_0(x))}{F'(G_0(x))}\pmod {x^n}
\]
于是这样不断迭代下去即可求出答案
但要注意当\(n=1\)时需要特殊处理（即递归边界）
那这个东西有什么用呢？以下举两个例子
多项式\(\exp\)
给出\(n-1\)次多项式\(f(x)\)，求\(g(x)\)满足
\[g(x)\equiv e^{f(x)}\pmod {x^n}
\]
系数均对\(998244353\)取模，保证\(f(0)=0\)
化一下柿子
\[\ln g(x)\equiv f(x)\pmod {x^n}\\
\Leftrightarrow \ln g(x)-f(x)\equiv 0\pmod {x^n}
\]
带入先前的牛顿迭代表达式可得
\[g(x)\equiv g_0(x)-\frac{\ln g_0(x)-f(x)}{\frac 1{g_0(x)}}\pmod {x^n}\\
g(x)\equiv g_0(x)(1-\ln g_0(x)+f(x))\pmod {x^n}\\
\]
迭代即可
递归边界\(g(x)\equiv 1\pmod x\),因为题目保证函数\(f(x)\)的常数项为\(0\)
代码如下
poly exp(int n,poly f)
{
if(n==1){poly g;g[0]=1;return g;}
poly g=exp(n+1>>1,f),h=ln(n,g);
for(int i=0;i<n;++i)h[i]=add(dec(0,h[i]),f[i]);
h[0]=add(h[0],1);
return mul(n,n,g,h);
}
多项式开根
给出\(n-1\)次多项式\(f(x)\)，求\(g(x)\)满足
\[g(x)\equiv \sqrt{f(x)}\pmod {x^n}
\]
系数均对\(998244353\)取模
仍然推柿子
\[g^2(x)\equiv f(x)\pmod {x^n}\\
g^2(x)-f(x)\equiv 0\pmod {x^n}
\]
还是带入牛顿迭代表达式可得
\[g(x)\equiv g_0(x)-\frac{g_0^2(x)-f(x)}{2g_0(x)}\pmod {x^n}
\]
多项式乘法+多项式求逆即可
递归边界\(g(x)\equiv\sqrt {f(0)} \pmod {998244353}\)
于是求出\(f(x)\)常数项的二次剩余即可
代码如下
inline poly sqr(int n,poly f)
{
if(n==1){poly g;g[0]=solve(f[0]);return g;}
poly g=sqr(n+1>>1,f),h,ivg;
ivg=ginv(n,g),h=mul(n,n,g,g);
int iv=qpow(2,mod-2);
for(int i=0;i<n;++i)ivg[i]=mll(iv,ivg[i]);
for(int i=0;i<n;++i)h[i]=dec(h[i],f[i]);
h=mul(n,n,h,ivg);
for(int i=0;i<n;++i)h[i]=dec(g[i],h[i]);
return h;
}
多项式除法+取模
这个稍微trivial一点
给出\(n-1\)次多项式\(f(x)\)和\(m-1\)次多项式\(g(x)\)，求\(q(x),r(x)\)满足
\[f(x)=q(x)g(x)+r(x)
\]
要求\(r(x)\)的次数小于\(m-1\)
系数均对\(998244353\)取模
对于多项式
\[F(x)=\sum_{i=0}^{n-1}a_ix^i
\]
我们定义
\[F_R(x)=\sum_{i=0}^{n-1}a_{n-i-1}x^i
\]
形象地说，将\(F(x)\)的系数倒过来
回到正题
\[\because f(x)=q(x)g(x)+r(x)\\
\therefore f(\frac 1x)=q(\frac 1x)g(\frac 1x)+r(\frac 1x)\\
\therefore x^{n-1}f(\frac 1x)=x^{n-1}q(\frac 1x)g(\frac 1x)+x^{n-1}r(\frac 1x)\\
\therefore x^{n-1}f(\frac 1x)=x^{n-m}q(\frac 1x)x^{m-1}g(\frac 1x)+x^{n-m+1}\cdot x^{m-2}r(\frac 1x)\\
\therefore f_R(x)=q_R(x)g_R(x)+x^{n-m+1}r_R(x)\\
\therefore f_R(x)\equiv q_R(x)g_R(x)\pmod {x^{n-m+1}}\\
\therefore q_R(x)\equiv \frac{f_R(x)}{g_R(x)}\pmod {x^{n-m+1}}
\]
于是多项式求逆+乘法就可以求出\(q(x)\)
那么
\[r(x)=f(x)-q(x)g(x)
\]
问题得以解决
求\(q(x)\)代码如下
inline poly div(int n,int m,poly f,poly g)
{
rv(n,f),rv(m,g);
g=ginv(n-m+1,g);
poly q=mul(n-m+1,n-m+1,f,g);
rv(n-m+1,q);return q;
}
多项式快速幂（普通版）
给定\(n-1\)次多项式\(f(x)\)和正整数\(k\),求\(g(x)\)满足
\[g(x)\equiv f^k(x)\pmod {x^n}
\]
系数均对\(998244353\)取模且保证\(f(0)=1\)
首先对于多项式函数\(f(x)\)满足\(f(0)=1\)证明如下命题：
\[f^p(x)\equiv 1\pmod {x^n}
\]
其中\(p\)是质数并且\(n<p\)
原命题等价于
\[(1+\sum_{i=1}^{n-1}a_ix^i)^p\equiv 1\pmod {x^n}\\
\Leftrightarrow 1^p+\sum_{i=1}^{n-1}a_i^px^{ip}\equiv 1\pmod {x^n}\\
\Leftrightarrow 1\equiv 1\pmod {x^n}\\
\]
其中第一步到第二步的变换可以由多项式定理来证明
于是
\[g(x)\equiv f^k(x)\equiv f^{k\%p}(x)\pmod {x^n}
\]
不妨令\(k'=k\%p\)
先两边同时求\(\ln\)
\[\ln g(x)\equiv \ln f^{k'}(x)\equiv k'\ln f(x)\pmod {x^n}
\]
再两边同时求\(\exp\)
\[g(x)\equiv e^{k'\ln f(x)}\pmod {x^n}
\]
于是就做完了
多项式快速幂（加强版）
同上，唯一区别在于不保证\(f(0)=1\)
这样会有什么影响呢?
回头一看发现如果不保证这一点那么\(\ln,\exp\)都没有办法做
于是考虑转化
我们需要找到\(f\)中最低的系数非零的项，记为\(a_tx^t\)，然后整个多项式除以\(a_tx^t\)，于是我们成功的让\(a_0\)变成了\(1\)，计算之后我们需要将答案右移\(t^k\)位，再乘\(a_t^k\)
但是还是有很多坑
- \(t^k\)如果大于等于\(n\)需要特判
- \(t^k,a_t^k\)中的\(k\)都应该对\(mod-1\)取模而不是\(mod\)
代码
inline poly fsp(int n,int k1,int k2,poly f)
{
int u,k;poly ans;
for(u=0;u<n&&!f[u];++u);k=qpow(f[u],k2);
if(1ll*u*k2>=n)return ans;
int iv=qpow(f[u],mod-2);
for(int i=u;i<n;++i)f[i]=mll(f[i],iv);
for(int i=0,j=u;j<n;++i,++j)ans[i]=f[j];
ans=ln(n,ans);
for(int i=0;i<n;++i)ans[i]=mll(ans[i],k1);
ans=exp(n,ans);
for(int i=0;i<u*k2;++i)f[i]=0;
for(int i=u*k2,j=0;i<n;++i,++j)f[i]=mll(ans[j],k);
return f;
}
int main()
{
int n,k1=0,k2=0,k3=0;scanf("%d",&n);pre(n);
scanf("%s",ch+1);int len=strlen(ch+1);
poly f;read(n,f);
for(int i=1;i<=len;++i)
{
k1=add(mll(10,k1),ch[i]^48),
k2=(10ll*k2%(mod-1)+(ch[i]^48))%(mod-1);
if(k1>n&&!f[0])//这里要特判
{
for(int i=0;i<n;++i)printf("0 ");
return 0;
}
}
print(n,fsp(n,k1,k2,f));
return 0;
}
第一代板子
封装后所有的完整代码
#include<bits/stdc++.h>
using namespace std;
const int mod=998244353,G=3,ivG=332748118,N=4e6+5;
inline int in()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
struct poly
{
vector<int>v;
inline int&operator[](int x)
{
while(x>=v.size())v.push_back(0);
return v[x];
}
inline void pre(int x,int lim)
{
int t=min(lim,(int)v.size());
for(int i=x;i<t;++i)v[i]=0;
}
};
namespace Math
{
int inv[N],pif;
inline int add(int x,int y){x+=y;return x>=mod?x-mod:x;}
inline int dec(int x,int y){x-=y;return x<0?x+mod:x;}
inline int mll(int x,int y){return 1ll*x*y%mod;}
struct pt
{
int x,y;
pt(int _x=0,int _y=0){x=_x,y=_y;}
inline pt operator*(const pt&rhs)
{
return pt(add(mll(x,rhs.x),mll(mll(y,rhs.y),pif)),add(mll(x,rhs.y),mll(y,rhs.x)));
}
};
inline int qpow(int x,int y)
{
int ans=1;
for(;y;y>>=1,x=mll(x,x))(y&1)&&(ans=mll(ans,x));
return ans;
}
inline pt qpow(pt x,int y)
{
pt ans=pt(1,0);
for(;y;y>>=1,x=x*x)if(y&1)ans=ans*x;
return ans;
}
inline void pre(int n)
{
inv[1]=1;
for(int i=2;i<=n;++i)inv[i]=mod-mll(mod/i,inv[mod%i]);
}
inline bool ck(int x){return qpow(x,(mod-1)>>1)==mod-1;}
inline int solve(int x)
{
int ans=0;
if(mod==2)return x;
if(!x)return 0;
else if(qpow(x,(mod-1)>>1)==mod-1)return -1;
int a=rand()%mod;
while(!a||!ck(dec(mll(a,a),x)))a=rand()%mod;
pif=dec(mll(a,a),x);
ans=qpow(pt(a,1),(mod+1)>>1).x;
return min(ans,mod-ans);
}//二次剩余求解
}
using namespace Math;
namespace Bas
{
int rev[N],wn[N];
inline void ntt(int lim,poly&f,bool tp)
{
for(int i=0;i<lim;++i)if(i<rev[i])swap(f[i],f[rev[i]]);
for(int mid=1;mid<lim;mid<<=1)
{
int sw=qpow(tp?ivG:G,(mod-1)/(mid<<1));
wn[0]=1;for(int i=1;i<mid;++i)wn[i]=mll(wn[i-1],sw);
for(int len=mid<<1,p=0;p+len-1<lim;p+=len)
for(int k=0;k<mid;++k)
{
int x=f[p+k],y=1ll*wn[k]*f[p+mid+k]%mod;
f[p+k]=add(x,y),f[p+mid+k]=dec(x,y);
}
}
}
inline poly mul(int n,int m,poly f,poly g)
{
int lim=1,l=0;while(lim<n+m)lim<<=1,++l;
for(int i=0;i<lim;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
f.pre(n,lim),g.pre(m,lim);
ntt(lim,f,0),ntt(lim,g,0);
for(int i=0;i<lim;++i)f[i]=mll(f[i],g[i]);
ntt(lim,f,1);int iv=qpow(lim,mod-2);
for(int i=0;i<lim;++i)f[i]=mll(f[i],iv);
return f;
}//乘法
inline void igl(int n,poly&f)
{
for(int i=n-1;i;--i)f[i]=mll(f[i-1],inv[i]);f[0]=0;
}//积分
inline void diff(int n,poly&f)
{
for(int i=0,t=f[i+1];i<n-1;++i,t=f[i+1])f[i]=mll(t,i+1);f[n-1]=0;
}//微分（注意这里写得不当很容易RE）
inline void rv(int n,poly&f){reverse(f.v.begin(),f.v.begin()+n);}
inline void read(int n,poly&f){for(int i=0;i<n;++i)f[i]=in();}
inline void print(int n,poly f){for(int i=0;i<n;++i)printf("%d ",f[i]);puts("");}
}
using namespace Bas;
namespace Poly
{
poly ginv(int n,poly f)
{
if(n==1){poly g;g[0]=qpow(f[0],mod-2);return g;}
poly g=ginv(n+1>>1,f),h,p=g;
int lim=1,l=0;while(lim<n+n)lim<<=1,++l;
for(int i=0;i<lim;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
f.pre(n,lim),p.pre(n,lim);
ntt(lim,f,0),ntt(lim,p,0);
for(int i=0;i<lim;++i)f[i]=mll(f[i],mll(p[i],p[i]));
ntt(lim,f,1);int iv=qpow(lim,mod-2);
for(int i=0;i<n;++i)h[i]=dec(add(g[i],g[i]),mll(f[i],iv));
return h;
}//多项式求逆
inline poly ln(int n,poly f)
{
poly g=ginv(n,f),h;diff(n,f);
h=mul(n,n,f,g);igl(n,h);
return h;
}//多项式求ln
poly exp(int n,poly f)
{
if(n==1){poly g;g[0]=1;return g;}
poly g=exp(n+1>>1,f);
poly h=ln(n,g);
for(int i=0;i<n;++i)h[i]=add(dec(0,h[i]),f[i]);
h[0]=add(h[0],1);
return mul(n,n,g,h);
}//多项式求exp
inline poly div(int n,int m,poly f,poly g)
{
rv(n,f),rv(m,g);
g=ginv(n-m+1,g);
poly q=mul(n,n-m+1,f,g);
rv(n-m+1,q);return q;
}//多项式除法求商式
inline poly sqr(int n,poly f)
{
if(n==1){poly g;g[0]=solve(f[0]);return g;}
poly g=sqr(n+1>>1,f),h,ivg;
ivg=ginv(n,g),h=mul(n,n,g,g);
int iv=qpow(2,mod-2);
for(int i=0;i<n;++i)ivg[i]=mll(iv,ivg[i]);
for(int i=0;i<n;++i)h[i]=dec(h[i],f[i]);
h=mul(n,n,h,ivg);
for(int i=0;i<n;++i)h[i]=dec(g[i],h[i]);
return h;
}//多项式开根
inline poly fsp(int n,int k1,int k2,poly f)
{
int u,k;poly ans;
for(u=0;u<n&&!f[u];++u);k=qpow(f[u],k2);
if(1ll*u*k2>=n)return ans;
int iv=qpow(f[u],mod-2);
for(int i=u;i<n;++i)f[i]=mll(f[i],iv);
for(int i=0,j=u;j<n;++i,++j)ans[i]=f[j];
ans=ln(n,ans);
for(int i=0;i<n;++i)ans[i]=mll(ans[i],k1);
ans=exp(n,ans);
for(int i=0;i<u*k2;++i)f[i]=0;
for(int i=u*k2,j=0;i<n;++i,++j)f[i]=mll(ans[j],k);
return f;
}//多项式快速幂
}
using namespace Poly;
char ch[N];
//上面所有的n都表示n-1次多项式
第二代板子
从未见过的船新版本：多项式板子第二代，常数大大优化，就是有亿点点难写，考场不建议使用（除非有板子）
#include<bits/stdc++.h>
using namespace std;
int nmsl;
namespace IO {
inline char nc(){
static char buf[500005],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,500000,stdin),p1==p2)?EOF:*p1++;
}
char out[500005],*pout=out,*eout=out+500000;
inline void flush() { fwrite(out,1,pout-out,stdout),pout=out; }
inline void pc(char c) { pout==eout&&(fwrite(out,1,500000,stdout),pout=out); (*pout++)=c; }
template<typename T> inline void put(T x,char suf) {
static char stk[40];int top=0;
x<0?pc('-'),x=-x:0; while(x) stk[top++]=x%10,x/=10;
!top?pc('0'),0:0; while(top--) pc(stk[top]+'0');
pc(suf);
}
template<typename T> inline T read(){
char ch=nc(); T sum=0; bool f=false;
for(;ch<'0'||ch>'9';ch=nc()) if(ch=='-') f=1;
while(ch>='0'&&ch<='9')sum=sum*10+ch-48,ch=nc();
return f ? -sum : sum;
}
}
#define Rint IO::read<int>()
using IO::put;
using IO::pc;
typedef vector<int> vec;
const int N=5e5+5,mod=167772161;
inline int add(int x,int y){return x+y>=mod?x+y-mod:x+y;}
inline void inc(int&x,int y){x=add(x,y);}
inline int dec(int x,int y){return x-y<0?x-y+mod:x-y;}
inline void rec(int&x,int y){x=dec(x,y);}
inline int qpow(int x,int y)
{
int ans=1;
for(;y;y>>=1,x=1ll*x*x%mod)
if(y&1)ans=1ll*ans*x%mod;
return ans;
}
namespace Cipolla
{
mt19937 rd(time(0));
int I,fl=0;
struct pt
{
int a,b;
pt(int _a=0,int _b=0){a=_a;b=_b;}
};
inline pt operator*(pt x,pt y)
{
pt ret;
ret.a=add(1ll*x.a*y.a%mod,1ll*x.b*y.b%mod*I%mod);
ret.b=add(1ll*x.a*y.b%mod,1ll*x.b*y.a%mod);
return ret;
}
inline bool check(int x){return qpow(x,(mod-1)/2)==1;}
inline int random(){return rd()%mod;}
inline pt qpow(pt a,int b)
{
pt ret=pt(1,0);
for(;b;a=a*a,b>>=1)if(b&1)ret=ret*a;
return ret;
}
inline int cipolla(int n)
{
if(!fl)srand(time(0)),fl=1;
if(!check(n)) return 0;
int a=random();
while(!a||check(dec(1ll*a*a%mod,n))) a=random();
I=dec(1ll*a*a%mod,n);
int ans=qpow(pt(a,1),(mod+1)/2).a;
return min(ans,mod-ans);
}
}
using namespace Cipolla;
namespace Preparation
{
int iv[N],top,rev[N],wn[N],up=1;
inline int glim(int n)
{
int l=0;
while(n)n>>=1,++l;
return l;
}
inline void pre(int x)
{
if(!top)iv[1]=1,top=2;
for(int i=top;i<=x;++i)
iv[i]=1ll*iv[mod%i]*(mod-mod/i)%mod;
if(top<x)top=x;
}
inline int ginv(int x){return x<=top?iv[x]:qpow(x,mod-2);}
inline void init(int l)
{
int lim=1<<l;
for(int i=0;i<lim;++i)
rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
for(int i=up;i<lim;i<<=1)
{
wn[i]=1;
int g=qpow(3,(mod-1)/(i<<1));
for(int j=1;j<i;++j)wn[i+j]=1ll*wn[i+j-1]*g%mod;
}
up=max(up,lim);
}
}
using namespace Preparation;
typedef unsigned long long ull;
namespace Container
{
struct poly
{
vec f;
inline poly(int w=0):f(1){f[0]=w;}
inline poly(const vec&_f):f(_f){}
inline int operator[](int x)const{return x<f.size()?f[x]:0;}
inline int&operator[](int x){if(x>=f.size())f.resize(x+1);return f[x];}
inline int size(){return f.size();}
inline void resize(int x){f.resize(x);}
inline poly slice(int x)const
{
if(x<f.size())return vec(f.begin(),f.begin()+x);
poly res(f);res.resize(x);
return res;
}
inline void read(int n){f.resize(n);for(int i=0;i<n;++i)f[i]=Rint;}
inline void print(int n){for(int i=0;i<n;++i)put(operator[](i),' ');pc('\n');}
inline poly diff()
{
vec res(f);
for(int i=0;i<res.size()-1;++i)res[i]=1ll*res[i+1]*(i+1)%mod;
res.pop_back();return res;
}
inline poly ing()
{
vec res(f);pre(res.size());res.push_back(0);
for(int i=res.size()-1;i;--i)res[i]=1ll*res[i-1]*ginv(i)%mod;
res[0]=0;return res;
}
inline poly rev()const
{
vec res(f);
reverse(res.begin(),res.end());
return res;
}
inline poly operator-()
{
vec res(f);
for(int i=0;i<res.size();++i)res[i]=dec(0,res[i]);
return res;
}
inline poly operator<<(const int k)const
{
vec res(f.size());
for(int i=k,j=0;i<res.size();++i,++j)res[i]=f[j];
return res;
}
inline poly operator>>(const int k)const
{
vec res(f.size());
for(int i=k,j=0;i<res.size();++i,++j)res[j]=f[i];
return res;
}
inline int ord()const
{
int pos=0;
while(pos<f.size()&&!f[pos])++pos;
return pos>=f.size()?-1:pos;
}
inline poly operator+(const poly&g)const;
inline poly operator-(const poly&g)const;
inline poly operator*(const int g)const;
inline poly operator*(const poly&g)const;
inline poly operator/(const int g)const;
inline poly operator/(const poly&g)const;
inline poly operator%(const poly&g)const;
inline poly mult(const poly&g,int sz,int tp)const;
inline poly inv()const;
inline poly div(const poly&h)const;
inline poly ln()const;
inline poly exp()const;
inline poly sqrt()const;
inline poly fsp(const int k)const;
};
inline poly poly::operator+(const poly&g)const
{
vec res(max(f.size(),g.f.size()));
for(int i=0;i<res.size();++i)res[i]=add(operator[](i),g[i]);
return res;
}
inline poly poly::operator-(const poly&g)const
{
vec res(max(f.size(),g.f.size()));
for(int i=0;i<res.size();++i)res[i]=dec(operator[](i),g[i]);
return res;
}
inline poly poly::operator*(const int y)const
{
vec res(f);
for(int i=0;i<res.size();++i)res[i]=1ll*res[i]*y%mod;
return res;
}
inline poly poly::operator/(const int y)const{poly F(f);return F*ginv(y);}
ull fr[N];
inline void ntt(poly&f,int lim,bool tp)
{
for(int i=0;i<lim;++i)fr[i]=f[rev[i]];
for(int mid=1,len=2;mid<lim;mid<<=1,len<<=1)
for(int j=0;j+len-1<lim;j+=len)
for(int k=0;k<mid;++k)
{
ull x=fr[j+k],y=fr[j+mid+k]*wn[mid+k]%mod;
fr[j+k]=x+y,fr[j+mid+k]=mod+x-y;
}
for(int i=0;i<lim;++i)fr[i]>=mod?fr[i]%=mod:0;
if(tp)
{
reverse(fr+1,fr+lim);
int t=ginv(lim);
for(int i=0;i<lim;++i)fr[i]=fr[i]*t%mod;
}
for(int i=0;i<lim;++i)f[i]=fr[i];
}
inline poly poly::operator*(const poly&g)const
{
poly F(f),G=g;
if(F.f.size()<=150&&G.f.size()<=150)
{
int p=f.size()+g.f.size()-1;vec res(p);
for(int i=0;i<p;++i)
for(int j=0;j<f.size()&&j<=i;++j)
inc(res[i],1ll*f[j]*G[i-j]%mod);
return res;
}
int l=glim(F.size()+G.size()-1),lim=1<<l;
init(l);F.resize(lim),G.resize(lim);
ntt(F,lim,0),ntt(G,lim,0);
for(int i=0;i<lim;++i)F[i]=1ll*F[i]*G[i]%mod;
ntt(F,lim,1);
return F.slice(f.size()+g.f.size()-1);
}
inline poly poly::mult(const poly&g,int sz,int tp)const
{
if(f.size()<=150&&g.f.size()<=150)
{
int p=f.size()+g.f.size()-1;p=min(p,sz);vec res(p);
for(int i=0;i<p;++i)
for(int j=i;j<f.size();++j)
inc(res[i],1ll*f[j]*g[j-i]%mod);
return res;
}
poly F(f),G=g.rev();
int k=G.size();
int l=glim(f.size()*tp),lim=1<<l;init(l);
ntt(F,lim,0),ntt(G,lim,0);
for(int i=0;i<lim;++i)F[i]=1ll*F[i]*G[i]%mod;
ntt(F,lim,1);int gg=g.f.size();
return vec(F.f.begin()+gg-1,F.f.begin()+gg+sz-1);
}
inline poly poly::inv()const
{
poly g(ginv(f[0])),g0,d;
for(int lim=2,l=1;(lim>>1)<f.size();lim<<=1,++l)
{
g0=g;init(l);d=slice(lim);
g0.resize(lim);
ntt(g0,lim,0),ntt(d,lim,0);
for(int i=0;i<lim;++i)d[i]=1ll*d[i]*g0[i]%mod;
ntt(d,lim,1);
fill(d.f.begin(),d.f.begin()+(lim>>1),0);
ntt(d,lim,0);
for(int i=0;i<lim;++i)d[i]=1ll*d[i]*g0[i]%mod;
ntt(d,lim,1);
g.resize(lim);
for(int i=lim>>1;i<lim;++i)g[i]=dec(g[i],d[i]);
}
return g.slice(f.size());
}
inline poly poly::div(const poly&h)const
{
if(f.size()==1)return 1ll*f[0]*ginv(h[0])%mod;
poly F(f),H=h;
int l=glim(F.size()),lim=1<<l,nlim=lim>>1;
poly G0=(H.slice(nlim)).inv(),Q0=slice(nlim);
init(l);ntt(G0,lim,0),ntt(Q0,lim,0);
for(int i=0;i<lim;++i)Q0[i]=1ll*Q0[i]*G0[i]%mod;
ntt(Q0,lim,1);Q0=Q0.slice(nlim);
poly Q=Q0;
ntt(H,lim,0);ntt(Q,lim,0);
for(int i=0;i<lim;++i)Q[i]=1ll*Q[i]*H[i]%mod;
ntt(Q,lim,1);
fill(Q.f.begin(),Q.f.begin()+nlim,0);
for(int i=nlim;i<lim;++i)Q[i]=dec(Q[i],F[i]);
ntt(Q,lim,0);
for(int i=0;i<lim;++i)Q[i]=1ll*Q[i]*G0[i]%mod;
ntt(Q,lim,1);
fill(Q.f.begin(),Q.f.begin()+nlim,0);
for(int i=0;i<lim;++i)Q[i]=dec(Q0[i],Q[i]);
return Q.slice(f.size());
}
inline poly poly::operator/(const poly&g)const
{
if(f.size()<g.f.size())return 0;
int p=f.size()-g.f.size()+1;
poly fr=rev(),gr=g.rev();
fr=fr.slice(p),gr=gr.slice(p);
return fr.div(gr).rev();
}
inline poly poly::operator%(const poly&g)const
{
poly F(f);return F.size()<g.f.size()?F:(F-(g*(F/g))).slice(g.f.size()-1);
}
inline poly poly::ln()const
{
poly F(f);
return ((F.diff()).div(F)).ing();
}
const int logB=4;
const int B=16;
namespace EXP
{
poly g[30][B];
inline void exp(const poly&f,poly&ret,int lim,int l,int r)
{
if(r-l<=128)
{
for(int i=l;i<r;++i)
{
ret[i]=(!i)?1:1ll*ret[i]*ginv(i)%mod;
for(int j=i+1;j<r;++j)inc(ret[j],1ll*ret[i]*f[j-i]%mod*(j-i)%mod);
}
return;
}
int k=(r-l)/B;
vector<long long>bl[B];poly T;
for(int i=0;i<B;++i)bl[i].resize(k<<1);
int len=1<<lim-logB+1,ll=lim-logB+1;
for(int i=0;i<B;++i)
{
if(i>0)
{
init(ll);
for(int j=0;j<(k<<1);++j)T[j]=bl[i][j]%mod;
ntt(T,len,1);
for(int j=0;j<k;++j)
inc(ret[l+i*k+j],T[j+k]);
}
exp(f,ret,lim-logB,l+i*k,l+(i+1)*k);
if(i<B-1)
{
for(int j=0;j<k;++j)T[j+k]=0,T[j]=ret[j+l+i*k];
init(ll);ntt(T,len,0);
for(int j=i+1;j<B;++j)
for(int t=0;t<(k<<1);++t)
bl[j][t]+=1ll*T[t]*g[lim][j-i-1][t];
}
}
}
}
inline poly poly::exp()const
{
poly F(f);
int mx=glim(F.size());
pre(1<<mx);
poly ret;ret.resize(1<<mx);
for(int lim=mx;lim>=8;lim-=logB)
{
int bl=1<<(lim-logB),tot=0,ll=1<<(lim-logB+1);
init(lim-logB+1);
for(int i=0;i<B-1;++i)
{
EXP::g[lim][i].resize(bl<<1);
for(int j=0;j<(bl<<1);++j)EXP::g[lim][i][j]=1ll*F[j+bl*i]*(j+bl*i)%mod;
ntt(EXP::g[lim][i],ll,0);
}
}
EXP::exp(*this,ret,mx,0,1<<mx);
return ret.slice(f.size());
}
inline poly poly::sqrt()const
{
poly g,h,gf,F1,F2,F3,F(f);
g[0]=cipolla(operator[](0));
h[0]=ginv(g[0]);
gf[0]=g[0];gf[1]=g[0];
int iv=(mod+1)/2;
init(0);
for(int lim=1,l=0;lim<f.size();lim<<=1,++l)
{
for(int i=0;i<lim;++i) F1[i]=1ll*gf[i]*gf[i]%mod;
ntt(F1,lim,1);
for(int i=0;i<lim;++i) F1[i+lim]=dec(F1[i],F[i]),F1[i]=0;
int nlim=lim<<1;init(l+1);
for(int i=lim;i<nlim;++i) rec(F1[i],F[i]);
F2=h;F2.resize(lim);
ntt(F1,nlim,0);ntt(F2,nlim,0);
for(int i=0;i<nlim;++i) F1[i]=1ll*F1[i]*F2[i]%mod;
ntt(F1,nlim,1);
for(int i=lim;i<nlim;++i) g[i]=dec(0,1ll*F1[i]*iv%mod);
if(nlim<f.size())
{
gf=g;
ntt(gf,nlim,0);
for(int i=0;i<nlim;++i) F3[i]=1ll*gf[i]*F2[i]%mod;
ntt(F3,nlim,1);
fill(F3.f.begin(),F3.f.begin()+lim,0);
ntt(F3,nlim,0);
for(int i=0;i<nlim;++i) F3[i]=1ll*F3[i]*F2[i]%mod;
ntt(F3,nlim,1);
for(int i=lim;i<nlim;++i) rec(h[i],F3[i]);
}
}
return g.slice(f.size());
}
inline poly poly::fsp(const int k)const
{
poly F(f);
int pos=F.ord();
if(pos<0)return 0;
int t=F[pos],len=F.size();
if(pos*k>len)return 0;
F=F>>pos;
F=F.slice(len-pos*k+1);
F=F/t;F=(F.ln()*k).exp();
pos*=k;F.resize(len);
F=F<<pos;
F=F*qpow(t,k);
return F;
}
}
using namespace Container;
namespace multiask
{
int a[N],m,n,ans[N];
const int M=1e5+5;
poly t[M<<2],F[M<<2];
#define lc rt<<1
#define rc rt<<1|1
void build(int rt,int l,int r)
{
if(l==r){t[rt][1]=dec(0,a[l]),t[rt][0]=1;return;}
int mid=(l+r)>>1;
build(lc,l,mid),build(rc,mid+1,r);
t[rt]=t[lc]*t[rc];
}
void ask(int rt,int l,int r)
{
if(l>=m)return;
if(l==r){if(l<m)ans[l]=F[rt][0];return;}
int mid=(l+r)>>1;
F[lc]=F[rt].mult(t[rc],mid-l+1,1);
F[rc]=F[rt].mult(t[lc],r-mid,1);
ask(lc,l,mid),ask(rc,mid+1,r);
}
#undef lc
#undef rc
inline void query(poly&f)
{
n=max(n,m);
build(1,0,n-1);
F[1]=f.mult(t[1].inv(),n,2);
ask(1,0,n-1);
}
inline void pre(int nn,int mm){n=nn,m=mm;}
}
namespace intpo
{
int n,xx[N],yy[N];
const int M=1e5+5;poly t[M<<2];
#define lc (rt<<1)
#define rc (rt<<1|1)
void build(int rt,int l,int r)
{
if(l==r){t[rt][1]=1,t[rt][0]=dec(0,xx[l]);return;}
int mid=(l+r)>>1;
build(lc,l,mid),build(rc,mid+1,r);
t[rt]=t[lc]*t[rc];
}
poly solve(int rt,int l,int r)
{
if(l==r){return 1ll*yy[l]*ginv(multiask::ans[l])%mod;}
int mid=(l+r)>>1;
poly lf=solve(lc,l,mid),rf=solve(rc,mid+1,r);
return t[rc]*lf+t[lc]*rf;
}
inline poly work()
{
build(1,0,n-1);multiask::pre(n,n);
for(int i=0;i<n;++i)multiask::a[i]=xx[i];
poly g=t[1].diff();multiask::query(g);
return solve(1,0,n-1);
}
#undef lc
#undef rc
}
NO PAIN NO GAIN
