MOSFET简介以及PMOS和NMOS的差异
最近在工作中,一直在调试关于MOSFET的电路。在设计过程中发现了PMOS和NMOS的差异,在此记录。
一、 MOSFET简介
MOSFET (metal-oxide-semiconductor field-effect transistor)的中文应称为"金属氧化物半导体场效应管"。从名字中就可看出这是一种场效应管,场效应管为我们带来了逻辑电路,从而有了计算机的物理实现。所有的场效应管的原则都是通过输入控制输出,具体来讲就是通过控制元件某部分的电压,来改变元件的导电性,从而改变流过元件中的电流。我在学习场效应管的时候看过一本国外教材,教材中用了一个水龙头的图片就让我茅塞顿开。我们可以这样想,被控制的元件就是水龙头,我们的控制信号就是打开水龙头的幅度,如果我们的信号足够强,水龙头就可以打开,水就会从水龙头中流出,这里的水就是元件中流出的电流。如果水龙头打开的幅度越大,那么水流量也必然变大,对应场效应管中加大控制信号,输出电流增大。当然,我们从生活中也知道水龙头打开的幅度是有极限的,因此水流量也有一个峰值,如果你仍然增大外力旋转阀门,最终只会造成不可逆的改变,阀门坏掉,控制失灵,水龙头只不过是水流的出口罢了。这对于场效应管同样适用,它有着自己的饱和区,如果控制电压足够大后,不管你如何增大电压,流出的电流都一定,但是如果电压过大,你也将会毁掉这个元件,失去控制。所以我习惯将场效应管称为"电水龙头"。

下面我们具体看看MOSFET的构造。首先,绝缘层(通常是二氧化硅)被覆盖在半导体(硅衬底)上,之后再在绝缘层上安置金属或多晶硅的门电极。因为二氧化硅是一种介电材料,这种构造非常像一个平行板电容器,只不过将一侧的金属板换成了半导体的硅衬底。以上描述的构造是MOS的部分,即金属-氧化物-半导体(metal-oxide-semiconductor)结构。对于半导体,我们知道它可按照掺杂类型分成P型半导体和N型半导体,前者导电载体为空穴,后者为电子。下面我们以P型半导体为例讲解。
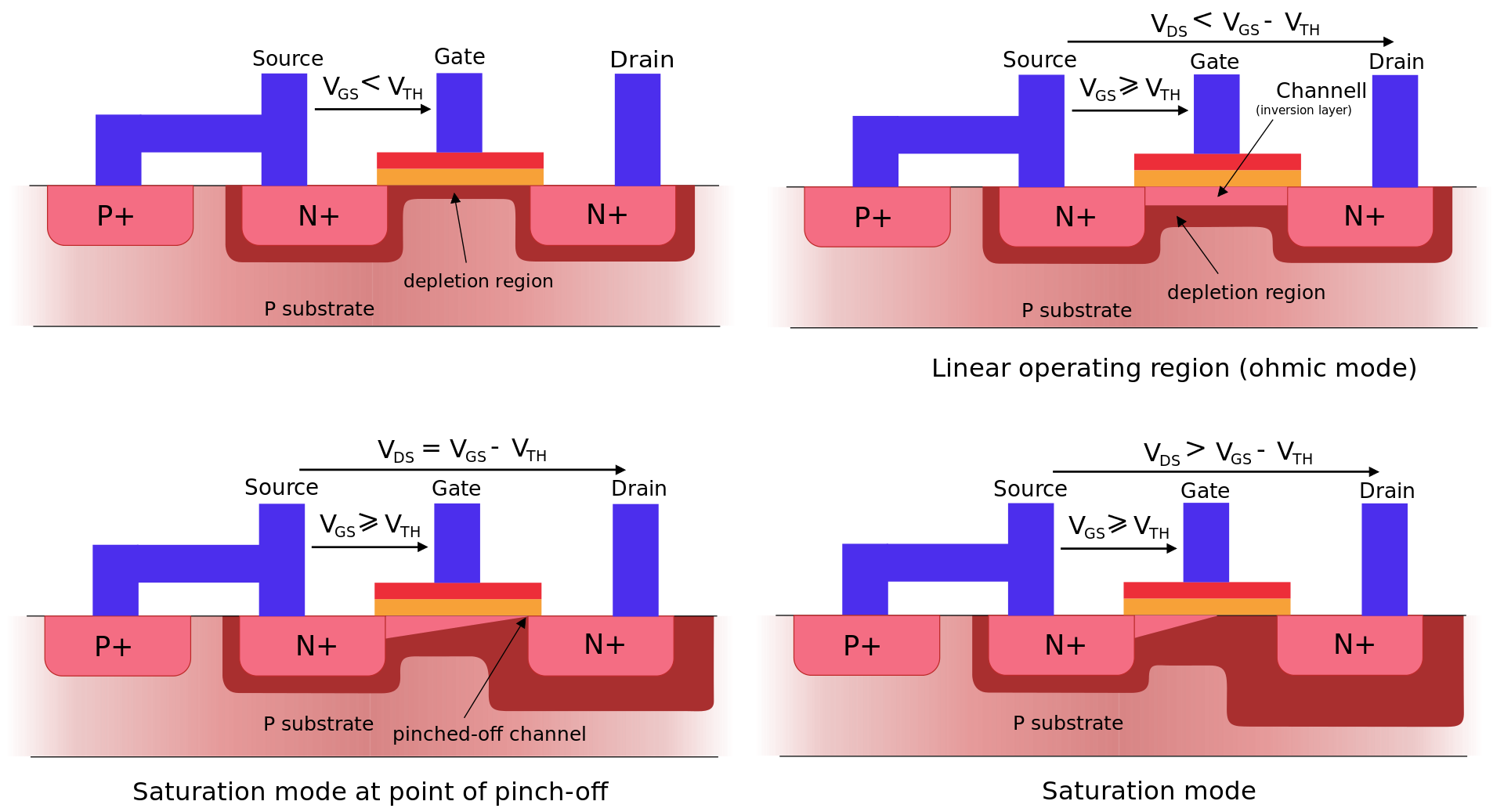
Ref: https://en.wikipedia.org/wiki/MOSFET
从上图中可以看出,MOS部分就是P衬底部分和gate(门极)间的部分。注意到Source(源极)和drain(漏极)部分掺杂和衬底相反。从半导体物理中我们知道,这会形成耗尽层(depeletion region),即这部分区域中无导电载荷存在。在初始情况下(Gate和source间无电压),耗尽层横亘与source和drain之间,相当于水龙头的阀门关上了,drain和source中的载流子无法传导,即在drain和source间无电流输出。如果我们增加gate和source间的电压$V_{GS}$,直到出现了右上图中的反转层(Inversion layer),此时drain和source连通,相当于水龙头的阀门打开了,drain和source间也将有电流$I_{DS}$流动。改变$V_{GS}$,反转层的厚度也将改变,从而改变drain和source间的电阻,达到了通过$V_{GS}$控制$I_{DS}$的效果。然而我们注意到这种情况是有条件的,仅限于$V_{DS}$不太大的情况下,如果$V_{DS}$过大,靠近drain的一侧便不可能形成反转层,就像右下图描绘的那样。你可能会认为这种情形无法导通电流了,但是drain和反转层之间的高电压会使电流继续导通,只不过在这个情形下,电流基本不受$V_{GS}$控制,类似于水龙头完全打开,电流饱和,故称为饱和区。总体上的导通情形可参考下图。
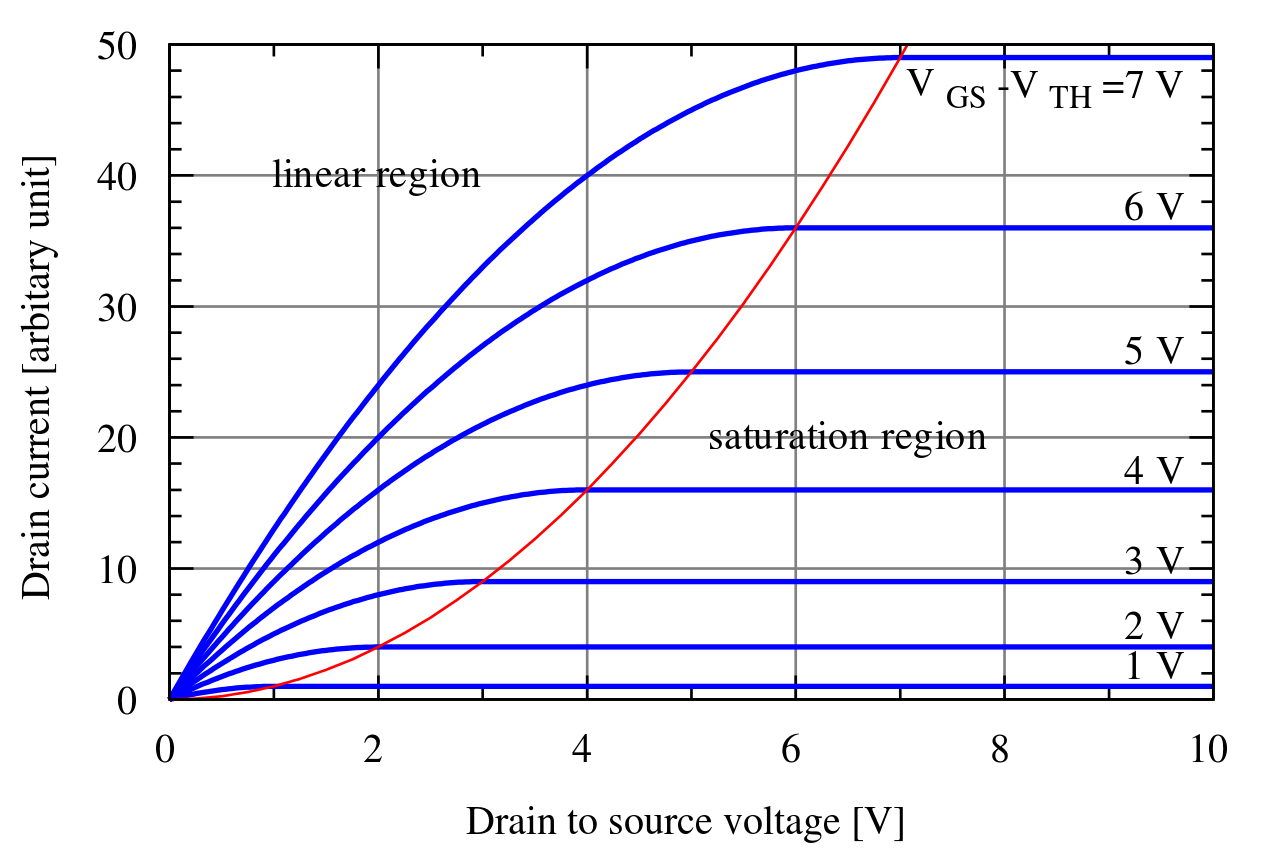
ref: https://en.wikipedia.org/wiki/MOSFET
对于NMOS:
在线性区($V_{GS}>V_T$,$V_{DS}\leq V_{GS}-V_T$),漏极电流$I_D=\mu_nC_{ox}\frac{W}{L}[(V_{GS}-V_T)V_{DS}-\frac12 V_{DS}^2]$. 这里$I_D$和控制电压$V_{GS}$线性相关,故名线性区。表达式中$\mu_n$是NMOS载荷电子的迁移率,$C_{ox}$是氧化物的电容,$W$是gate极板的宽度,$L$是gate极板的长度,这里长度也是源极和漏极的间距,宽度是在另一维度的度量。
在饱和区 ($V_{GS}>V_T$,$V_{DS}\geq V_{GS}-V_T$),$I_D=\frac12\mu_nC_{ox}\frac{W}{L}(V_{GS}-V_T)^2$.
对于PMOS:
阈值电压为负,导通时$V_{GS}<0$。
类似地,在线性区($V_{SG}>|V_T|$,$V_{SD}<V_{SG}-|V_T|$),漏极电流$I_D=\mu_p C_{ox}\frac{W}{L}[(V_{SG}-|V_T|)V_{SD}-\frac12 V_{SD}^2]$. 这里$\mu_p$是PMOS的载荷空穴的迁移率。
在饱和区($V_{SG}>|V_T|$,$V_{SD}>V_{SG}-|V_T|$),$I_D=\frac12\mu_p C_{ox}\frac{W}{L}(V_{SG}-|V_T|)^2$.
上面的公式对应MOSFET的理想模型。针对实际模型,我们做出如下修正(以NMOS为例)。
(1) 在$V_{GS}<V_T$时,因为氧化物中电流泄露,漏极电流$I_D$并不为0。这种泄露效应在越薄的氧化层中越明显。
(2)在饱和区,从上面的分析我们也看到了,当$V_{DS}$增加时,反转层的长度减少了,即$L$减少了,因此漏极电流应相应增大。我们引入参数$\lambda$,修正这一效应,此时漏极电流可表示为
$I_D=\frac12\mu C_{ox}\frac{W}{L}(1+\lambda V_{DS})(V_{GS}-V_T)^2$.
(3)Body effect: P型半导体处彻底的电极又称为Body. 其上施加的电压会影响阈值电压$V_T$. 具体来讲,$V_T$实际上和$V_{SB}$相关,即Source和Body的电势差。
(4)温度效应: MOSFET很多参数都与温度相关。
二、 PMOS和NMOS的差异
一直以来我都忽视了PMOS和NMOS的差异,只在概念上明白PMOS的载荷是空穴,NMOS的载荷是电子。因此在设计电路时往往将一些元件的参数同时应用于两者,但最近在一个电路测试的过程中我发现我的电路只适用于PMOS不适用于NMOS。这让我有些不解,请教了一个大师,大师仅让我将gate处的电阻提高3倍,以此提高增益(gain)。我不理解它都没怎么看电路怎么就能得出3倍这个结论,于是再次请教。原来答案是空穴的速度是电子速度的三分之一,也就是迁移率的比例。按他的建议改进了电路,果然有效,对他真是十分佩服,也深感要理解透彻才能达到这个地步!我现在的程度只能对MOSFET介绍这么多,将来有时间希望从费米面和能带理论入手好好分析一下电子元件,从而加深认识与理解。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号