82同路径(62)

作者: Turbo时间限制: 1S章节: 动态规划

晚于: 2020-09-02 12:00:00后提交分数乘系数50%

截止日期: 2020-09-09 12:00:00

问题描述 :

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

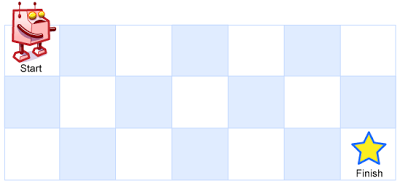
例如，上图是一个7 x 3 的网格。有多少可能的路径？

 

示例 1:

输入: m = 3, n = 2

输出: 3

解释:

从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向右 -> 向下

2. 向右 -> 向下 -> 向右

3. 向下 -> 向右 -> 向右

 

示例 2:

输入: m = 7, n = 3

输出: 28

 

输入说明 :

输入m和n，以空格分隔

1 <= m, n <= 100

题目数据保证答案小于等于 2 * 10 ^ 9

 

输出说明 :

输出一个整数

输入范例 :

7 3

输出范例 :

28

#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
    int uniquePaths(int m, int n) 
    {
        vector<vector<int>> dp(n,vector<int>(m,0));
    //    int dp[n][m];
        for(int i=0;i<m;i++)
            dp[0][i]=1;//把第一列赋值 
        for(int i=0;i<n;i++)
            dp[i][0]=1;//第一行赋值 
        for(int i=1;i<n;i++)
        {
            for(int j=1;j<m;j++)
            {
                dp[i][j]=dp[i-1][j]+dp[i][j-1]; 
            } 
        }
        return dp[n-1][m-1];
    }
};
int main()
{
    int m,n;
    cin>>m>>n;
    int res=Solution().uniquePaths(m,n);
    cout<<res;
    return 0;
}