聊聊递归和尾递归

聊聊递归和尾递归

就个人而言，在学习递归时，不知云里雾里，很难理解，一直想着这个递归的完整过程应该是个什么样子，然后就越陷越深，陷入局部观中。在看了《数据结构与算法之美》的递归章节后，正如王争老师所说的:

当我们看到递归时，我们总想把递归平铺展开，脑子里就会循环，一层一层往下调，然后再一层一层返回，试图想搞清楚计算机每一步都是怎么执行的，这样就很容易被绕进去。

对于递归代码，这种试图想清楚整个递和归过程的做法，实际上是进入了一个思维误区。很多时候，我们理解起来比较吃力，主要原因就是自己给自己制造了这种理解障碍。

那么正确的思维方式应该是什么样子的呢？

王争老师也给出了解答：

如果一个问题 A 可以分解为若干子问题 B、C、D，你可以假设子问题 B、C、D 已经解决，在此基础上思考如何解决问题 A。而且，你只需要思考问题 A 与子问题 B、C、D 两层之间的关系即可，不需要一层一层往下思考子问题与子子问题，子子问题与子子子问题之间的关系。屏蔽掉递归细节，这样子理解起来就简单多了。

编写递归代码的关键是，只要遇到递归，我们就把它抽象成一个递推公式，不用想一层层的调用关系，不要试图用人脑去分解递归的每个步骤。

因此我们主要是将递归的事物抽象成为一个递推公式，屏蔽递归细节即可。

进入正题

说到递归，有几个条件需要满足：

  1. 一个问题的解可以分为几个子问题

    何为子问题？子问题就是数据规模更小的问题。比如，在电影院中，你想要直到“自己在哪一排”，可以分解为“前一排的人在哪一排”这样一个子问题。

  2. 子问题和原问题除了规模不同，求解思路都相同

    还是电影院那个例子，你求解“自己在哪一排”的思路，和前面一排人求解“自己在哪一排”的思路，是一模一样的。

  3. 存在递归终止条件

    把问题分解为子问题，把子问题再分解为子子问题，一层一层分解下去，不能存在无限循环，这就需要有终止条件。还是电影院的例子，第一排的人不需要再继续询问任何人，就知道自己在哪一排，也就是 f(1)=1，这就是递归的终止条件。

下面举个例子来说明：

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。

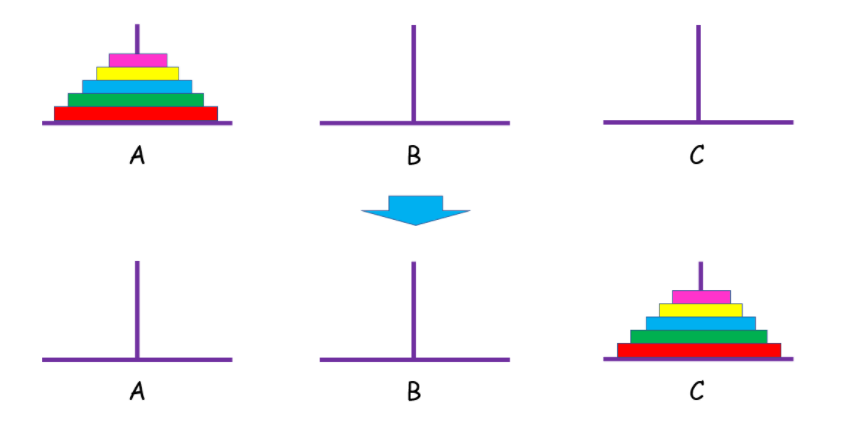
image-20211129205642809

  1. 可以发现当只有一个圆盘时，也就是递归终止条件，我们只需要把圆盘直接由A柱移动到C柱，即A->C
  2. 对于多个圆盘时，我们就需要进行分析了，如果我们能将初始A柱上面的前n-1个圆盘移动到B柱上并且保持顺序不变，然后将A柱上的第n个圆盘移动C上，接着将B柱上的n-1个圆盘在移动到C柱上，这样就满足条件了。你可能会问：“那 n - 1 个圆盘是怎么从 A 移到 C 的呢？”注意，当你在思考这个问题的时候，就将最初的 n 个圆盘从 A 移到 C 的问题，转化成了将n-1个圆盘从 A 移到 C 的问题， 依次类推，直至转化成 1 个盘子的问题时，问题也就解决了。也就是将原问题分解成若干个与原问题结构相同但规模较小的子问题。

代码如下：

package main

import "fmt"
/*
参数：
n 圆盘个数
a A柱 
b B柱
c C柱
*/
func HanoiTower(n int,a,b,c string) {
	// f(1)的情况  （递归终止条件）
	if n == 1 {
		fmt.Println(a,"->",c)
		return
	}

	// 把前n-1个原盘从a柱移动到b柱   子问题采用递归
	HanoiTower(n-1,a,c,b)
	// 将第n个圆盘由a柱直接移动到c柱
	fmt.Println(a,"->",c)
	// 再把前n-1个圆盘从b柱移动到c柱  子问题采用递归
	HanoiTower(n-1,b,a,c)
}

func main() {
	n := 3
	a,b,c := "a","b","c"

	HanoiTower(n,a,b,c)
}

测试结果如下：

a -> c
a -> b
c -> b
a -> c
b -> a
b -> c
a -> c

递归代码要警惕堆栈溢出

上面编写的递归代码还算是规模很小的，如果遇上规模大的代码，就会遇到很多问题，比如堆栈溢出。而堆栈溢出会造成系统性崩溃，后果会非常严重。为什么递归代码容易造成堆栈溢出呢？

函数调用会使用栈来保存临时变量，每调用一个函数时，都会将临时变量封装为栈帧压入内存栈中，函数调用完成之后，才出栈。系统栈或者虚拟机栈空间一般都不大，如果递归求解的数据规模很大，调用层次很深，一直压入栈，就会有堆栈溢出的风险。

我们又该如何预防堆栈溢出呢？

  1. 可以在代码中限制递归的深度，超过该深度直接报错（但是允许的递归深度和当前线程剩余的栈空间大小有关，事先无法计算。如果实时计算，代码过于复杂，就会影响代码的可读性。）
  2. 采用尾递归优化，尾递归是指出现在递归函数尾部直接返回递归函数结果的递归。

尾递归优化

我们从上面预防堆栈溢出的方案里看到了尾递归这一选项，刚刚的递归还没缓一缓呢，怎么又冒出一个尾递归？

接下来让我慢慢道来：

了解尾递归首先要知道什么是尾调用？

尾调用的概念非常简单，一句话就能说清楚，就是指某个函数的最后一步是调用另一个函数。

func f(x int) func(i int) {
	return t(x)
}

上面代码中，函数f的最后一步是调用函数g，这就叫尾调用。尾调用不一定出现在函数尾部，只要是最后一步操作即可。

尾调用之所以与其他调用不同，就在于它的特殊的调用位置。

函数调用会在内存形成一个"调用记录"，又称"调用帧"（call frame），保存调用位置和内部变量等信息。如果在函数A的内部调用函数B，那么在A的调用记录上方，还会形成一个B的调用记录。等到B运行结束，将结果返回到A，B的调用记录才会消失。如果函数B内部还调用函数C，那就还有一个C的调用记录栈，以此类推。所有的调用记录，就形成一个"调用栈"(call stack）。

img

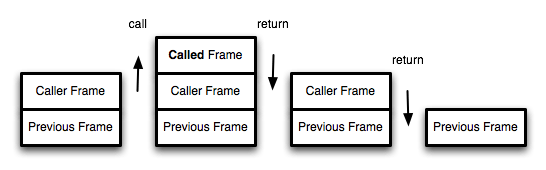
尾调用由于是函数的最后一步操作，所以不需要保留外层函数的调用记录，因为调用位置、内部变量等信息都不会再用到了，只要直接用内层函数的调用记录，取代外层函数的调用记录就可以了。

函数调用自身，称为递归。如果尾调用自身，就称为尾递归。

递归非常耗费内存，因为需要同时保存成千上百个调用记录，很容易发生"栈溢出"错误（stack overflow）。但对于尾递归来说，由于只存在一个调用记录，所以永远不会发生"栈溢出"错误。

说了那么多，下面我们实操一下对比递归和尾递归的性能差异看看。

Fibonacci数列的递归与尾递归对比

递归求Fibonacci数列对于我们来说并不陌生了，分分钟就可以把代码写出来

// Fibonacci 普通递归
func Fibonacci(n int) int {
	if n == 0 || n == 1 {
		return 1
	}

	return Fibonacci(n-1) + Fibonacci(n-2)
}

我们可以对其调用过程进行简单的一个分析，如下所示：

Fibonacci(5)
{Fibonacci(4)+Fibonacci(3)}
{{Fibonacci(3)+Fibonacci(2)}+{Fibonacci(2)+Fibonacci(1)}}
{{{Fibonacci(2)+Fibonacci(1)}}+{Fibonacci(1)+Fibonacci(0)}}+{Fibonacci(1)+Fibonacci(0)}+1}
{{{{Fibonacci(1)+Fibonacci(0)}+1}}+{1+1}}+{1+1+1}} 
{{{{1+1}+1+{1+1}}+{1+1+1}}
{{{2+1}+2}}+3}
{{3+2}+3}
{5+3}
8

很容易看出, 因为递归式使用了运算符，每次重复的调用都使得运算的链条不断加长，系统不得不使用栈进行数据保存和恢复。

如果每次递归都要对越来越长的链进行运算，那速度极慢，并且可能栈溢出，导致程序奔溃。

所以有了尾递归的写法：

// TailFibonacci 尾递归
// 尾部递归是指递归函数在调用自身后直接传回其值，而不对其再加运算，效率将会极大的提高。
func TailFibonacci(n int,a1,a2 int) int {
	if n == 0 {
		return a1
	}

	return TailFibonacci(n-1,a2,a1+a2)
}

它的递归过程如下：

F(5,1,1)
F(4,1,1+1)=F(4,1,2)
F(3,2,1+2)=F(3,2,3)
F(2,3,2+3)=F(2,3,5)
F(1,5,3+5)=F(1,5,8)
F(0,8,5+8)=F(0,8,13)
8

可以发现没有递归那么长的链进行运算，直接调用自身后返回其值。

尾递归函数的特点是在回归过程中不用做任何操作，这个特性很重要，因为大多数现代的编译器会利用这种特点自动生成优化的代码。减少不必要的堆栈生成，使得程序栈维持固定的层数，不会出现栈溢出的情况。

下面使用benchmark进行测试

package main

import "testing"

func BenchmarkFibonacci(b *testing.B) {
	for i := 0; i < b.N; i++ {
		Fibonacci(10)
	}
}

func BenchmarkTailFibonacci(b *testing.B) {
	for i := 0; i < b.N; i++ {
		TailFibonacci(10,1,1)
	}
}

在命令行输入以下命令

go test bench .

结果如下：

goos: windows
goarch: amd64
pkg: base/algorithm/recursion
cpu: AMD Ryzen 7 4800U with Radeon Graphics
BenchmarkFibonacci-16            3916202               300.9 ns/op
BenchmarkTailFibonacci-16       40975909                29.17 ns/op

PASS
ok      base/algorithm/recursion        5.280s

可以发现，Fibonacci的递归版为300.9 ns/op，而尾递归版则为29.17 ns/op。差距还是很明显的

结语

开头我们提到了，写递归时不要试图想清楚整个过程，这样会陷入误区，我们只需要把它抽象成一个递推公式，屏蔽递归细节。

在递归中，往往一不小心就容易造成内存栈的溢出操作，我们既可以在代码中限制递归的深度，也可以采用尾递归的方式进行优化。性能的提升还是很明显的。

References:

posted @ 2021-11-29 22:22  无_忧  阅读(158)  评论(0)  编辑  收藏  举报