树状数组总结 【非原创】
参考博客:
树状数组的用途就是维护一个数组,重点不是这个数组,而是要维护的东西,最常用的求区间和问题,单点更新。但是某些大牛YY出很多神奇的东西,完成部分线段树能完成的功能,比如区间更新,区间求最值问题。
树状数组当然是跟树有关了,但是这个树是怎么构建的呐?这里就不得不感叹大牛们的脑洞之大了,竟然能想出来用二进制末尾零的个数多少来构建树以下图为例:
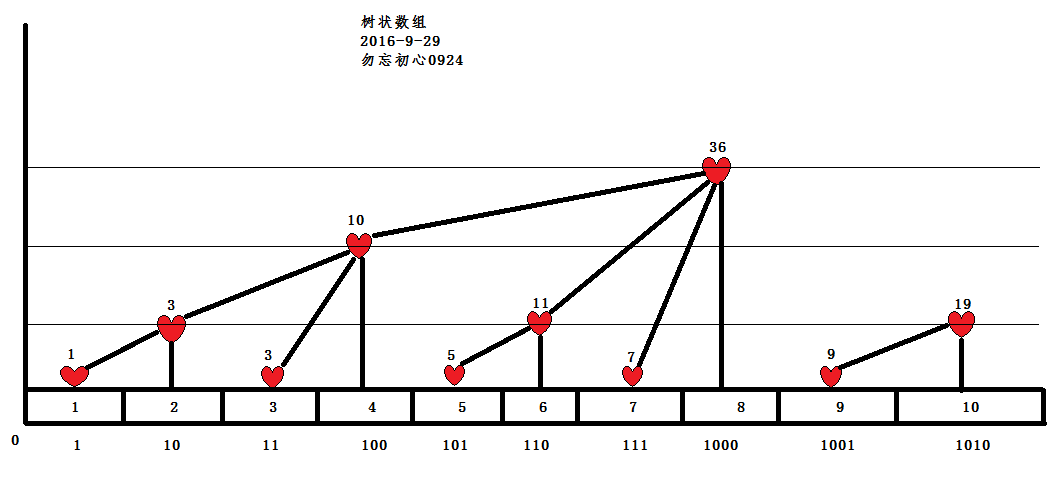
从上图能看出来每一个数的父节点就是右边比自己末尾零个数多的最近的一个,也就是x的父节点就是x+(x&(-x)),这里为什么可以参考计算机位运算,x&(-x)就能得出自己末尾0的个数例如10&(-10)=(0010)二进制。每一个节点保存的就是以他为根节点的数的和,这样就得出来了更新树状数组的函数:
int lowbit(int x)
{
return x&(-x);
}
void uodate(int x)
{
while(x<Max)
{
c[x]+=val;
x+=lowbit;
}
}
树状数组虽然将数据用树形结构组织起来的但是还是很乱怎么办呐?实际上树状数组维护的是数组的前缀和,比如sum(x)就是a[x]的前缀和,想查询l~r区间的元素和只需要求出来sum(r)-sum(l-1),这里的sum函数十分的神奇:
{
int s=0;
while(x>0)
{
s+=c[x];
x-=lowbit;
}
return s;
}
x-(x&(-x))刚巧是前一个棵树的根节点,这样就能求出1到x和,以x=9为例,9&(-9)=1;这样x-(x&(-x))=8,刚巧是前一棵树的根节点。
例题:poj 2352 stars http://poj.org/problem?id=2352;
题意给你n个星星的坐标,每一个星星的等级为:在不在这个星星右边并且不比这个星星高的星星的个数
然后出处每个等级星星的个数
树状数组,一开始把上一个题的模板扒过来的......真是伤啊,这个题更新点的时候要把右边的点更新到MAXN要不然会漏掉条件的
*/
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<string>
#include<algorithm>
#define N 32010
using namespace std;
int n;
int c[N];
int cur[N];//统计每个等级的星星
int lowbit(int x)
{
return x&(-x);
}
int getx(int x)
{
int ans=0;
while(x>0)
{
ans+=c[x];
x-=lowbit(x);
}
return ans;
}
void update(int x)
{
while(x<=N)
{
c[x]++;
x+=lowbit(x);
}
}
int main()
{
//freopen("in.txt","r",stdin);
int x,y;
while(scanf("%d",&n)!=EOF&&n)
{
memset(cur,0,sizeof cur);
memset(c,0,sizeof c);
for(int i=1;i<=n;i++)
{
scanf("%d%d",&x,&y);
update(x+1);
//for(int j=1; j<=n; j++)
// cout<<c[j]<<" ";
//cout<<endl;
//cout<<getx(x+1)-1<<endl;
cur[getx(x+1)-1]++;
}
//cout<<endl;
for(int i=0;i<n;i++)
printf("%d\n",cur[i]);
}
return 0;
}
然后就是更高层次的操作了,区间更新。
【一些基础】
差分数组:
设原数组是a[n],差分数组c[n],c[i]=a[i]-a[i-1],那么明显地a[i]=sigma(c,i),如果想要修改a[i]到a[j](比如+v),只需令c[i]+=v,c[j+1]-=v
【主要内容】
我们可以实现NlogN时间的“单点修改,区间查询”,“区间修改,单点查询”,其实后者就是前者的一个变形,要明白树状数组的本质就是“单点修改,区间查询”
怎么实现“区间修改,区间查询”呢?
观察式子:
a[1]+a[2]+...+a[n]
= (c[1]) + (c[1]+c[2]) + ... + (c[1]+c[2]+...+c[n])
= n*c[1] + (n-1)*c[2] +... +c[n]
= n * (c[1]+c[2]+...+c[n]) - (0*c[1]+1*c[2]+...+(n-1)*c[n]) (式子①)
那么我们就维护一个数组c2[n],其中c2[i] = (i-1)*c[i]
每当修改c的时候,就同步修改一下c2,这样复杂度就不会改变
那么
式子① =n*sigma(c,n) - sigma(c2,n)
于是我们做到了在O(logN)的时间内完成一次区间和查询
例题:戳这里

1 //树状数组(升级版) 2 #include <cstdio> 3 #define lowbit(x) (x&-x) 4 #define ll long long 5 #define maxn 200010 6 using namespace std; 7 ll n, q, c1[maxn], c2[maxn], num[maxn]; 8 void add(ll *r, ll pos, ll v) 9 { 10 while(pos <= n) 11 { 12 r[i] += v; 13 pos += lowbit(pos); 14 } 15 } 16 ll sigma(ll *r, ll pos) 17 { 18 ll ans; 19 for(ans=0;pos;pos-=lowbit(pos))ans+=r[pos]; 20 return ans; 21 } 22 int main() 23 { 24 ll i, j, type, a, b, v, sum1, sum2; 25 scanf("%lld",&n); 26 for(i=1;i<=n;i++) 27 { 28 scanf("%lld",num+i); 29 add(c1,i,num[i]-num[i-1]); 30 add(c2,i,(i-1)*(num[i]-num[i-1])); 31 } 32 scanf("%lld",&q); 33 while(q--) 34 { 35 scanf("%lld",&type); 36 if(type==1) 37 { 38 scanf("%lld%lld%lld",&a,&b,&v); 39 add(c1,a,v);add(c1,b+1,-v); 40 add(c2,a,v*(a-1));add(c2,b+1,-v*b); 41 } 42 if(type==2) 43 { 44 scanf("%lld%lld",&a,&b); 45 sum1=(a-1)*sigma(c1,a-1)-sigma(c2,a-1); 46 sum2=b*sigma(c1,b)-sigma(c2,b); 47 printf("%lld\n",sum2-sum1); 48 } 49 } 50 return 0; 51 }
接着就是RMQ算法,用来求区间最值,直接求当然是不现实的,因为数据很多的时候,复杂度太高,这样就要先进性预处理,dp[i][j]表示从i开始2^j范围内的最值,这样能推出状态转移方程 dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1)][j-1])或者min(dp[i][j-1],dp[i+(1<<(j-1)][j-1])。怎么得出来这个方程的呐?就是以i为起点2^j的状态能由以i为起点到2^j这个范围的中点2^(j-1)左右两个部分的最值得到。
首先是预处理部分:
void RMQ_init(int n)
{
for(int j=1;j<20;j++)
for(int i=1;(i+(1<<j)-1)<=n;i++)
{
dp1[i][j]=max(dp1[i][j-1],dp1[i+(1<<(j-1))][j-1]);
dp2[i][j]=min(dp2[i][j-1],dp2[i+(1<<(j-1))][j-1]);
}
}
然后是查询
int RMQ(int L,int R)
{
int k=(int)(log(R-L+1.0)/log(2.0));
return max(dp1[L][k],dp1[R-(1<<k)+1][k]);或者return min(dp2[L][k],dp2[R-(1<<k)+1][k]);
}
查询是什么原理呐?就是l到r的长度内取k的最大值使得2^k<(r-l+1);这样查询l到l+2^k内的最值和r-2^k到r内的最值,虽然中间有些元素有些重复但是不会影响正确结果,但是查询区间和的时候就不能这么重复了。
例题 士兵杀敌(三)http://acm.nyist.net/JudgeOnline/problem.php?pid=119
#include <bits/stdc++.h>
#define N 100010
using namespace std;
int dp1[N][20];//存放最大值
int dp2[N][20];//存放最小值
int n,m,a;
int l,r;
void RMQ_init(int n)
{
for(int j=1;j<20;j++)
for(int i=1;(i+(1<<j)-1)<=n;i++)
{
dp1[i][j]=max(dp1[i][j-1],dp1[i+(1<<(j-1))][j-1]);
dp2[i][j]=min(dp2[i][j-1],dp2[i+(1<<(j-1))][j-1]);
//cout<<"dp1[i][j]="<<dp1[i][j]<<endl;
//cout<<"dp2[i][j]="<<dp2[i][j]<<endl;
}
}
int RMQ(int L,int R)
{
int k=(int)(log(R-L+1.0)/log(2.0));
//cout<<"max(dp1[L][k],dp1[R-(1<<k)+1][k])="<<max(dp1[L][k],dp1[R-(1<<k)+1][k])<<endl;
//cout<<"min(dp2[L][k],dp2[R-(1<<k)+1][k])="<<min(dp2[L][k],dp2[R-(1<<k)+1][k])<<endl;
return max(dp1[L][k],dp1[R-(1<<k)+1][k])-min(dp2[L][k],dp2[R-(1<<k)+1][k]);
}
int main()
{
//freopen("C:\\Users\\acer\\Desktop\\in.txt","r",stdin);
//memset(dp1,0,sizeof dp1);
//memset(dp2,0,sizeof dp2);
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&dp1[i][0]);
dp2[i][0]=dp1[i][0];
}
RMQ_init(n);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&l,&r);
printf("%d\n",RMQ(l,r));
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号