2016012025小学四则运算练习软件项目报告
本项目报告结构一览:
一.前言
二.需求分析
三.功能设计
四.设计实现
五.算法详解(代码展示部分包含在其中)
六.测试运行
七.不足与改进
八.项目总结
九.PSP展示
十.后记
代码仓库地址:https://git.coding.net/honey_xiaoxinxin/Calculate.git,测试效果见与src同目录的result.txt文件
一.前言
连续沉浸在代码的世界里几天,其中,有某一模块功能实现的欣喜,有调试很久还是找不到错误原因的烦躁,有不断发现问题解决问题的思考与进步,等等等等......但是,当终于完成了项目,我开始写这篇博客时,有的,是满满的收获和成就感。希望这篇博客能给我自己和大家带来启发和帮助。
二.需求分析
在这里我想首先给出一个需求分析的定义:需求分析就是了解、判断用户需要什么、想最终达到什么目的、怎么实现,为你们提供产品、服务、项目等提供目标和检验标准。
接下来我从这几个方面进行了需求分析:
1.编写目标:完成面向小学生的,由3-5个运算符组成的四则混合运算的出题和解题(使用java语言)使小学生的运算能力得到充分的锻炼。
2.用户的特点:该程序的最终用户为小学生。根据小学生的知识储备和能力,可以得出编程过程中我们需要注意的点:
(1) 每个数字不能过大,运算符不能过多。由此也可与功能要求中题目属性对应:每个数字在0-100之间,运算符3-5之间
(2) 运算过程中不能出现负数(做减法时注意)
(3) 运算过程中不能出现非整数(做除法时注意,结果只能是整数)
3.假定和约束
编写开发时间约束:11天
编写代码要求:使用java语言
4.需求规定
(1)业务需求:程序可接收一个输入参数n,然后随机产生n道加减乘除(分别使用符号+-*÷来表示)练习题,注意除号的表示方法,每个数字在 0 和 100 之间,运算符在3个到5个之间。每个练习题至少要包含2种运算符。同时,由于小学生没有分数与负数的概念,你所出的练习题在运算过程中不得出现负数与非整数,练习题生成好后,将生成的n道练习题及其对应的正确答案输出到文件“result.txt”中。
(2)用户需求:对于本题,我认为用户需求和业务需求是等同的
(3)功能需求:见功能设计
三.功能设计
1.基本功能:实现四则混合运算的出题和计算(注意对运算符个数和种数的要求)
2.扩展功能:
(1)带括号的四则运算:需注意括号的出现是否有意义(前面是加减,后面是乘除,括号的出现才是有意义的)
(2)支持真分数的出题与运算:需注意分数可以自动化简(包括出题中出现分数的化简和结果的化简);计算过程与结果都必须是真分数(即控制运算过程中的值是大于0,小于1的)

四.设计实现
(一)整体思路:
- 基本四则运算:先产生两个数字一个运算符的四则运算,再进一步产生运算符连接它们,组成含3-5个运算符的题目。再将题目这个字符串中的数字和运算符拆分,利用两个栈来把题目转化为后缀表达式,再利用栈运算此后缀表达式得出答案。
- 加括号的四则运算:在基本版的基础上,增加遇到括号时拆分题目这个字符串时的操作,相应增加遇到左括号和右括号时的入栈和出栈操作。
- 真分数加减:先产生两个真分数,并运算这两个真分数,在运算结果符合要求的情况下,继续产生一个真分数与刚才所得的结果进行运算,知道产生3-5个运算符时结束。采用边产生边运算边判断的模式,避免了不符合题目条件式子的出现。运算过程中同样要注意对产生分数和每次结果的化简。
我整体只用了一个类。想通过一个类不同的方法的调用实现功能。
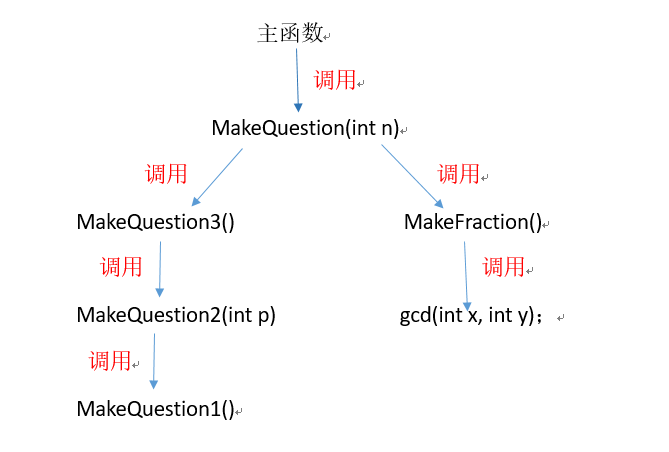
(二)我设计的函数:
- 实现最简单两个数四则运算题目的方法:MakeQuestion1();
- 实现一个含3-5个(至少两种)运算符的四则运算题目的方法MakeQuestion2(int p);
- 实现一个混合四则运算题目计算的方法:MakeQuestion3();
- 实现产生和计算真分数加减的方法:MakeFraction();
- 实现产生两个数最大公因数的方法(用于真分数化简):gcd(int x, int y);
- 实现产生规定个数(输入的n)四则运算与真分数运算的函数:MakeQuestion(int n);
(三)函数间的逻辑关系
五.算法详情
1.生成题目的算法
(1)先利用MakeQuestion1()生成两个数的加减乘除运算,再生成最基本的题目时,就要注意减法不能出现负数,除法不能出现余数。那如何来把保证这两点呐?我的部分代码如下:
int a = (int) (Math.random() * 100);// 产生100以内的随机数 int b = (int) (Math.random() * 100); int c = (int) (Math.random() * 4);// 产生整数0到3 if (c == 1) {// 如果是“-”,保证a比b大,避免出现负数 if (a < b) { int temp = a; a = b; b = temp; } } if (c == 3) {// 如果是除法,保证能整除 b = (int) (Math.random() * 20) + 1; a = (int) (Math.random() * 6) * b; }
(2) 接着我在MakeQuestion2(int p)(参数p是在MakeQuestion3()中随机生成的,表示调用MakeQuestion1()的次数,以保证运算符是随机的3-5个)中随机产生一个连接运算符,并调用MakeQuestion1();连续几次以保证运算符数量。这里为了保证最后的结果符合要求,连接符号的选择是“+”或者“*”。并且当前面是加减,后面是乘的时候,产生括号。保证了括号有效性的问题。这样就产生了一道题目,并把题目保存在一个字符串中。部分如下:
if (con.equals("*")) { String com = MakeQuestion1(); if (flag == 1) {//如果前面是加减后面是乘除的话,加括号 question += "(" + com + ")" + con; } else { question += com + con;//生成一个最简运算式子,和符号 } } else { question += MakeQuestion1() + con; }
2.解答题目的算法
(1)在解答题目时,我的总体思路也是把中缀表达式转为后缀表达式,再进行运算。
①首先我认为这里的一个难点就是怎么把question这个字符串中的数字和符号区分开来。我这里利用了两个参数k,j遍历字符串进行了区分。
②解题时利用了两个栈。一个存放数字和后来进入的操作符;一个存放操作符,并对操作符进行优先级处理。遇到数字直接放到number栈中。
遇到操作符,判断如果是左括号或者操作符栈为空,直接入operate操作符栈;如果栈顶是左括号或者要入栈操作符比栈顶符号优先级高,直接入栈;如果是右括号,弹出符号并压入number栈,直到遇到左括号,并且左括号不入number栈;其他情况,则先弹出operate栈顶元素,压入number栈,再将下一个操作符入operate栈。
③遍历完question字符串,如果operate栈不空的话,把剩余元素全都压入number栈。这样number栈中就形成了后缀表达式,把栈中元素存到一个数组中,但由于栈是先入后出的,所以逆序遍历数组才是真正的后缀表达式。逆序遍历的同时,再利用number这个栈进行运算,遇到数字直接入栈,遇到运算符从栈中弹出两个数字进行运算,并把结果压入栈中,如此最终留在栈中的元素即为运算结果。
以下为此算法的代码:
public void MakeQuestion3() {//运算混合四则运算方法,利用栈实现 Stack<String> number = new Stack<String>();//创建一个存储数字或符号的栈 Stack<Character> operate = new Stack<Character>();//创建一个存储操作符的栈 int p = (int) (Math.random() * 2) + 2;// p则是产生简单等式的次数,这里取2或3,以保证运算符为3个或5个 String question = MakeQuestion2(p);//调用方法MakeQuestion2(p);产生一个四则运算题目 int len = question.length(); int k = 0;//k是遍历字符串的一个参数 int same=0; for (int j = -1; j < len - 1; j++) {//把题目字符串进行拆分,拆分出数字和运算符,分别进行存储 if (question.charAt(j + 1) == '+' || question.charAt(j + 1) == '-' || question.charAt(j + 1) == '*' || question.charAt(j + 1) == '÷' || question.charAt(j + 1) == '(' || question.charAt(j + 1) == ')' || j == len - 2) { if (j == -1) {//如果第一个就是运算符,即左括号,存储在操作符栈中 operate.push(question.charAt(0)); } else if (j == len - 2) {//如果到字符串的最后了,直接存储到数字栈中 number.push(question.substring(k)); break; } else { if (k <= j) { number.push(question.substring(k, j + 1));//是数字的话存储到数字这个栈中 } if (operate.empty() || question.charAt(j + 1) == '(') {//操作符栈为空或者接下来的符号是左括号的话都直接存储到操作符栈中 operate.push(question.charAt(j + 1)); } else if ((operate.peek() == '+' || operate.peek() == '-') && (question.charAt(j + 1) == '*' || question.charAt(j + 1) == '÷')) { operate.push(question.charAt(j + 1));//如果将要放入栈中的运算符优先级比栈顶元素高,直接入栈 } else if (operate.peek() == '(') {//栈顶是左括号的话,下一个操作符也直接入栈 operate.push(question.charAt(j + 1)); } else if (question.charAt(j + 1) == ')') {//下一个操作符是右括号的话,弹出操作符栈顶元素并压入数字栈中 number.push(String.valueOf(operate.pop())); if (!operate.empty()) { operate.pop(); } } else {//操作符是同等优先级的时候,把栈顶元素弹出压入数字栈中,并把下一个操作符压入操作符栈中 if(operate.peek()==question.charAt(j + 1)){ same++; } number.push(String.valueOf(operate.pop())); operate.push(question.charAt(j + 1)); } } k = j + 2; } } if(same==p+2){//判断题目的符号是否都相同 ifsame=1; } while (!operate.empty()) {//最后把操作符栈中剩余的元素都压入数字栈中 number.push(String.valueOf(operate.pop())); } String[] result = new String[20]; int k1 = 0; while (!number.empty()) {//把数字栈中的元素也就是形成的后缀表达式存储在数组中 result[k1] = number.pop(); k1++; } for (k1 = k1 - 1; k1 >= 0; k1--) {//逆序遍历数组,运算得到的后缀表达式 if (!result[k1].equals("+") && !result[k1].equals("-") && !result[k1].equals("*") && !result[k1].equals("÷")) {//是数字的话,先压入栈中 number.push(result[k1]); } else { int a1 = 0; int b1 = 0; if (!number.empty()) {//弹出两个数进行相应运算 b1 = Integer.parseInt(number.pop()); } if (!number.empty()) { a1 = Integer.parseInt(number.pop()); } if (result[k1].equals("+")) {//如果是加号的话,弹出两个数相加 int c1 = a1 + b1; number.push(String.valueOf(c1)); } else if (result[k1].equals("-")) { int c1 = a1 - b1; number.push(String.valueOf(c1)); } else if (result[k1].equals("*")) { int c1 = a1 * b1; number.push(String.valueOf(c1)); } else { int c1 = a1 / b1; number.push(String.valueOf(c1)); } } } if(ifsame==1){//如果全部符号都相等的话,不输出题目 ; }else{ System.out.println(question + " = " + number.pop());//最后输出问题和答案 } }
(2) 在遍历question这个题目字符串的同时,我同时对它的符号进行了判断,如果符号都相同的话使ifsame这个标志参数为1,避免产生只含一种运算符的题目。
3.产生和运算真分数的方法
由于真分数加减没有优先级的限制,所以我们可以边生成题目,边进行运算,以保证运算结果一定是真分数。先随机产生两个真分数,并保证它们是最简的,再随机生成运算符,对他们进行加减运算。把运算结果保存起来,再生成一个真分数,与刚才的运算结果再进行运算。直到运算符数目符合要求。这部分代码也是我比较满意的部分,以下为部分代码展示:
int count = (int) (Math.random() * 2) + 3;// 随机产生运算符的数目 for (int u = 0; u < count; u++) {// 小于运算符数量时不断产生分数,不断计算 int denominator2 = (int) (Math.random() * 19) + 1;// 生成分母 int numerator2 = (int) (Math.random() * 20);// 生成分子 if (numerator2 != 0) { if (numerator2 > denominator2) {// 避免不是真分数 int temp = numerator2; numerator2 = denominator2; denominator2 = temp; } if (numerator2 == denominator2) {// 如果分子等于分母,重新生成分子 numerator2 = (int) (Math.random() * 20); } int gcd2 = gcd(numerator2, denominator2);// 化简分式,使其最简 denominator2 = denominator2 / gcd2; numerator2 = numerator2 / gcd2; } int symbol = (int) (Math.random() * 2);// 随机产生运算符 if (op2[symbol].equals("+")) {// 如果是加号,实现分数加法 if (denominator1 == denominator2) {// 如果两个分母相同,直接将分子相加 numerator = numerator1 + numerator2; } else {// 通分,相加 denominator = denominator1 * denominator2; numerator = numerator1 * denominator2 + numerator2 * denominator1; } if (denominator < numerator) {// 如果运算结果不是真分数 u--;// 计数的u减一,也就是重新生成重新计算 } else {// 在给定范围内的话,通分运算结果 int gcd = gcd(numerator, denominator); denominator = denominator / gcd; numerator = numerator / gcd; question1 += op2[symbol] + numerator2 + "/" + denominator2;// 把题目进行完善 denominator1 = denominator;// 储存运算结果到denominator1和numerator1 numerator1 = numerator; } } else {// 如果是减号,实现减法操作 if (denominator1 == denominator2) {// 分母相同直接分子相减 numerator = numerator1 - numerator2; } else {// 其他情况,先通分再相减 denominator = denominator1 * denominator2; numerator = numerator1 * denominator2 - numerator2 * denominator1; } if (numerator < 0) {// 如果导致结果小于0了,就重新生成 u--; } else {// 通分结果化简 int gcd = gcd(numerator, denominator); denominator = denominator / gcd; numerator = numerator / gcd; question1 += op2[symbol] + numerator2 + "/" + denominator2; denominator1 = denominator;// 储存通分结果 numerator1 = numerator; } } }
4.求两数最大公因数算法
在分数化简时就用到了此算法。这里用了递归实现:
public int gcd(int x, int y) {// 求最大公因数的函数 if (x == 0) { return y; } else { return gcd(y % x, x); } }
六.测试运行
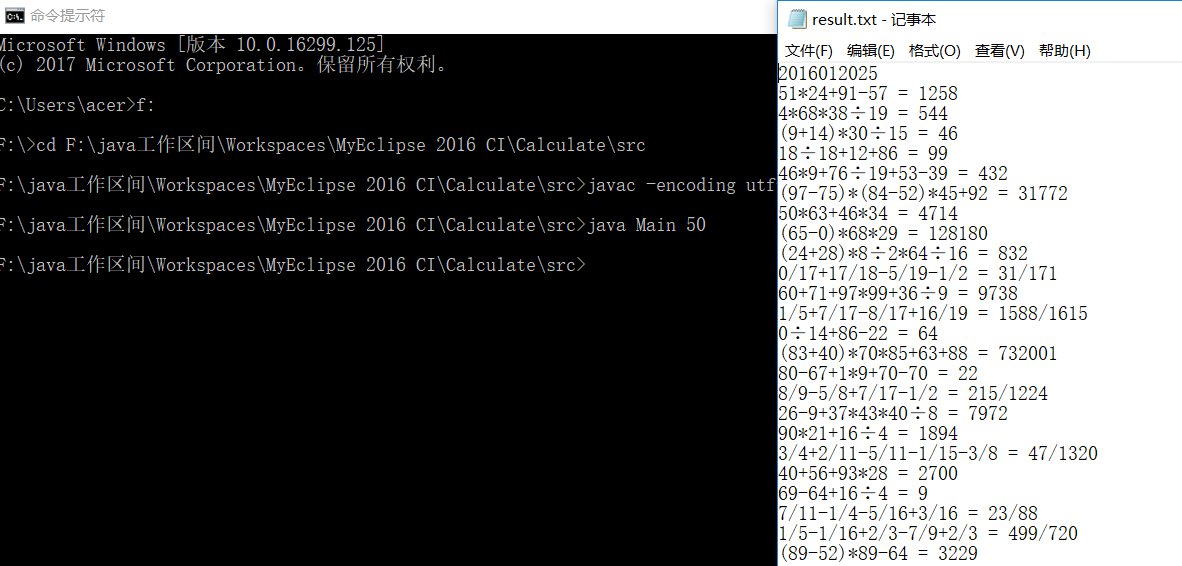
进入src文件下,输入javac -encoding utf-8 Main.java 编译出相应的class文件,再输入java Main 50进行测试:
1.正确的输入
2.错误的输入:

七.不足与改进
虽然我在项目书写过程中,不断改进发现的问题和不足,但项目仍存在一些不足:
1.在正整数出题的过程中,由于我先生成了简单的式子再用运算符将他们拼接,导致了运算符的数目为3个或5个,无法出现四个运算符的情况。这个问题在开始采用这种方式出题时我就想到了,解决的办法的话,我觉得可以在产生三个运算符后,不再调用MakeQuestion1(),而是手动产生一个符号和一个随机数。但是觉得产生3个或5个已经算是随机个数了,不需要为了刻意满足四个运算符而额外加多代码量,就没有对这个问题再进行改进。
2.由于最开始看题目要求时不够仔细,没有看到老师推荐的调度场算法。虽然我的实现整体思路和调度场算法是一样的。但是用了两个栈来得到后缀表达式,导致后缀表达式出栈存储到数组后,需要逆序遍历数组。这里走了一些弯路。
3.还有一个问题就是,在产生括号时,我可以出现多对括号,但是没有产生多重括号,这里也是一个我值得改进的地方。我也会再继续思考,完善代码。
八.项目总结
1.我书写代码的过程采用了“逐步求精”的写法,以方法为一个功能块进行编程,通过方法间的逐级调用实现了整个功能。函数间的调用见上面第四点设计实现。我认为这样子编写给调试和测试都带来了很多便利,同时也增加了我代码的可移植性和可读性。(软件设计的'模块化'原则的体现)
2.项目整体上实现了基本功能和拓展功能。比较系统的完成了预期的效果,但仍存在很多不足和问题,我也对这些不足进行了分析,也会不断对我的项目进行改进。
3.项目实现的过程要比我想象中艰难,花费的时间也是远远超过我的预期。但也让我从中收获到很多,不断发现问题,分析问题,解决问题的过程也让我对java语言有了更好的应用和理解。
九.PSP展示
|
PSP |
任务内容 |
计划时间(min) |
完成时间(min) |
|
Planning |
计划 |
10 |
8 |
|
Estimate |
估计这个任务需要多少时间,并规划大致工作步骤 |
8 |
10 |
|
Development |
开发 |
300 |
660 |
|
Analysis |
需求分析 |
20 |
25 |
|
Design Spec |
生成文档 |
0 |
0 |
|
Design Review |
设计复审 |
0 |
0 |
|
Coding Standard |
代码规范 |
5 |
5 |
|
Design |
具体设计 |
40 |
60 |
|
Coding |
具体编码 |
180 |
420 |
|
Code Review |
代码复审 |
30 |
35 |
|
Test |
测试 |
25 |
115 |
|
Reporting |
报告 |
160 |
400 |
|
Test Report |
测试报告 |
120 |
360 |
|
Size Measurement |
计算工作量 |
10 |
10 |
|
Postmortem & Process Improvement Plan |
事后总结, 并提出过程改进计划 |
30 |
30 |
(1)整个项目中,写代码和修改代码的时间比我预计的要长好多。在我按照自己脑中的想法写出我认为对的代码后,运行起来总是报错。我用debug调试代码也花费了大量的时间。
(2)开始对整个项目的要求和理解还是不够充分,导致做到一半又发现自己忽略了一个要求或者没有实现某个要求。
(3)写博客的时间我也想分享一下,本来的我的计划是用2小时写完博客,并自己总结一下自己整个项目的表现。但是实际上我用了6小时左右才写完博客的基本版,后来也在不断改进。但是我并不认为这是一件不好的事,在写博客的过程中,也让我重新梳理了自己的思路,对我项目中的优点和不足有了更深的理解。
十.后记
很感谢这个项目填充了我的这几天。这个项目带给了我很多收获。在编写的过程中,遇到了很多不懂的地方,都通过百度解决了问题,使我对java语言有了更深入的了解;其次在项目调试的过程中,也让我对debug的使用更加熟练了。历经一整个周末终于敲出自己相对满意的程序还是很有成就感的。我也一定会继续努力,继续加油,不断改进自己的项目!





