寒假集训学习记录 1-20

　　嗯，作为一个大一才接触acm的弱鸡，发现那些大佬们又厉害又谦虚（主要是尽然还有空水群，水群简直快乐极了，呜呜呜），我一水群时间就过的飞快，然后就更菜，陷入一个解不出来的死循环，嗯，然后就菜的没谱，呜呜呜……

　　然后呢，今天的内容就是并查集，我觉得有点难以弄懂，说不定多写写就能领悟了呢。

　　首先并查集的概念：可以进行合并和查找的的集合，字面意思吧，就是。然后看看官方一点的解释，在计算机科学中，并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。并查集存在两个操作和一个需要解答的问题。

　　关于合并的实现：就是在合并时将元素所在深度小的集合合并到元素所在深度大的集合里面去，嗯，网上借鉴了一个图

      

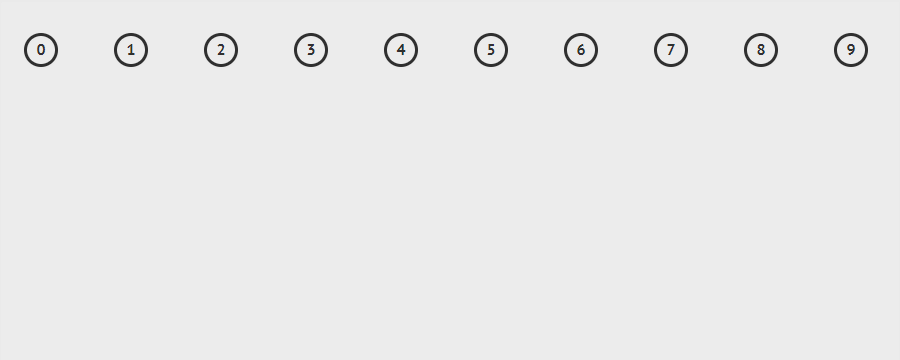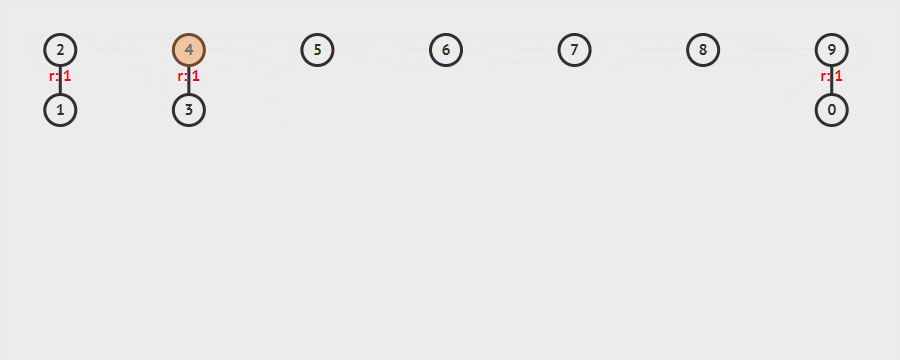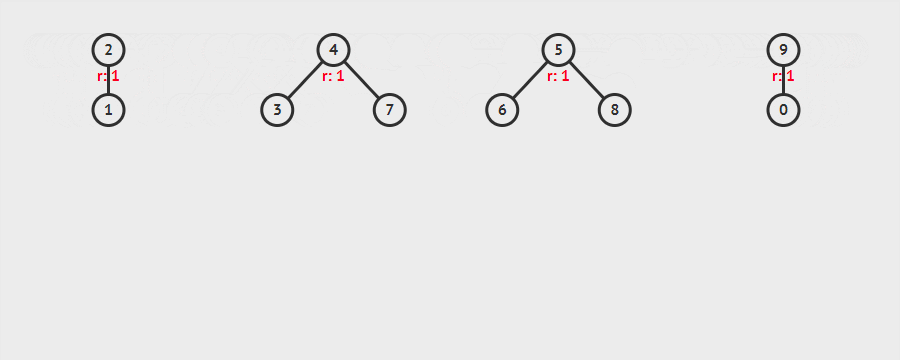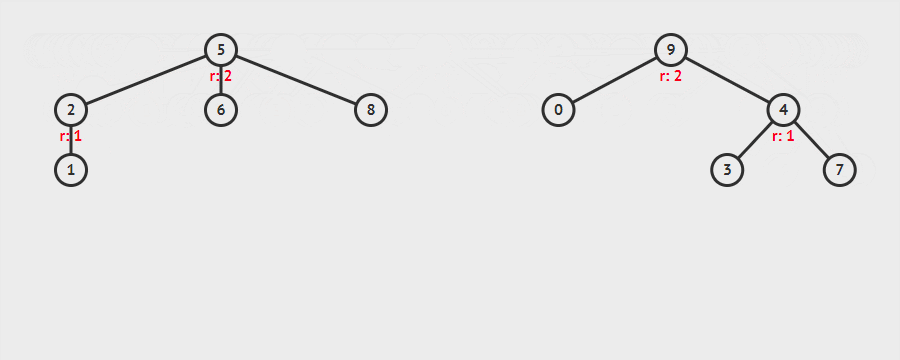
　　那我们如何实现并查集这种数据结构呢，第一，初始化元素  第二，实现元素与元素之间的联合操作   第三，实现查找元素所在树的根节点  第四，解决一个问题，判断两个元素是不是在同一个树上(两个元素是否连接)。现在我满五年直接看一道题，

假设县上有五个镇（1 2 3 4 5），修了三条公路，
如下：
1 ，2
3 ，4
2 ，5
问还需要修多少条路才能使各个镇的路都连接起来

　　当然这道题由于只有五个镇的原因，需要连通起来所需路径条数很容易就能看出来了，但是当镇很多，路也很多的情况呢，这个时候就需要代码来实现了，

　　首先创建并查集集合：　　

void union_op(int x,int y){
    if(std::max(x,y)>len_-1){
        std::cout<<"input is invalid"<<std::endl;
    }
    if(union_set_[x]!=union_set_[y]){
        union_set_[y]=union_set_[x];
    }
}

　　合并操作：

void union_op(int x, int y) {
    if (std::max(x, y) > len_-1) {
       std::cout << "input is invalid" << std::endl;
    }
    if (union_set_[x] != union_set_[y]) {
      union_set_[y] = union_set_[x];
    }
  }

最后是查找：

int find_op(int target) {
 // TODO(check) 
    int father = union_set_[target]; 
    if (father == target) return target;
    while (father != union_set_[father]) {
     father = union_set_[father];
     }
     return father;
 }   
     int find1_op(int target) {
     // TODO(check)
     int father = union_set_[target];
     if (father == target) return target;
     return find1_op(father);
 }　　额， 好像出问题了，写不了了，那就乘机再仔细看看吧，还有路径优化呢。然后小废物结尾。