OO-第一单元总结
由于寒假没能好好学习java,pre也没有提前开始,所以导致第一单元的三次作业都特别赶,最后也只是通过了第一次作业,二三两次都没能通过中测。
哎,所以也就这次机会好好总结一下这一个单元收获到的东西。
第一次作业:
第一次作业要求实现一个简单多项式求导,而且只存在幂函数和常数函数组合而成的表达式以及一些空白项。因为不存在表达式的嵌套,不存在括号之类的。所以除了数字(系数、指数、常数)所带的符号之外,项与项之间的连接是通过加减号来实现的。于是每一项之间就只有常数和幂函数的乘积形式,最终也一定能通过指数的加减和系数的乘积最终化简为幂次函数的形式--a*x^b(^就是指数符号,替换掉了原来的**),其中对a、b均可以为0。化简完后,再通过一些处理,可以把连接项的符号全变成+号,-号可以放在后一项的系数中去。然后就是一项一项的把字符串变成一个一个的Item类放入容器中存起来,最后遍历所有的Item类,返回自己的导数,通过连接符连接起来就能得到最后的结果。
类复杂度:
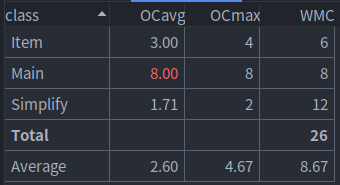
方法复杂度:
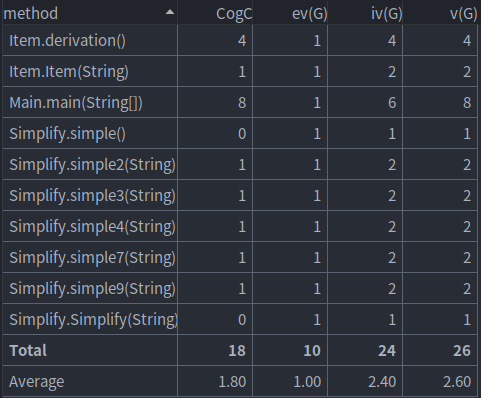
所以我一共创建了三各类,一个是负责读入要求导的表达式和输出导函数字符串的主类(Main.class),一个是负责对输入字符串进行化简分割的Simplify类,最后就是一个项Item类。
Main类的功能主要是输入、分割项和输出。
其中分割项的代码如下:
1 String[] strings = last.split("[+]"); 2 Item[] items = new Item[strings.length]; 3 for (int i = 1; i < strings.length; i++) { 4 items[i] = new Item(strings[i]); 5 }
Simplify主要就是实现字符串的化简功能,把每一项都化简为a*x^b的形式(第一次作业基本是面向过程做的)
最后一个Item类主要是实现求导功能
Item类:
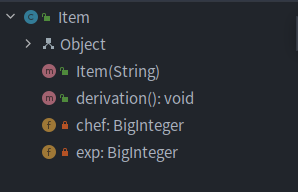
存放了系数和指数,求导时就直接利用系数指数进行计算,进而实现derivation功能。(a*x^b)'=a*b*x^(b-1)
hack攻略:
第一次作业中,没有自己写评测机,所以大部分数据都是手动构造的,导致成功率特别低,我认为,还是要通过随即生成数据来进行测试,再加上一些人为手动构造的特殊数据, 这样才能提高找出bug的可能性。
第二三次作业思路:
虽然没能通过课下的测试,但写了这么久,也还是想说一说自己的思路。
首先是通过递归i下降进行表达式的解析,整体是一个最大的表达式,把所有的项都找出来放在一个容器内,然后项是一大串因子的乘积,也是同样在递归下降的过程中找到每一项中所有的factor,对于factor,分别创建常数类、三角类、幂函数类和表达式因子类。表达式因子类和表达式类的解析方法相同,只不过是多了一队括号。解析完后,在对每一个类定义一个求导法则,表达式类求导-->项求导相加-->(项求导==每个因子求导乘其他因子的求和,返回值是一个多项式类)-->因子求导则是通过各自的求导方法实现(其中表达式类因子则直接调用表达式类的求导)。
递归下降大致过程:
get(表达式)-->get(项)+get(+|-)...
get(项)->get(因子)+get(*)...
get(因子) -->get(sin类cos类幂函数类常数类表达式因子类)
get(表达式因子类)->get(左括号)+get(b表达式类)+get(右括号)
其他因子类类似
求导过程:
表达式求导<--每一项求导相加(表达式类)
项求导<--(每一个因子求导*其他因子)求和(表达式类)
因子求导<-多种因子的乘积(项类)
心得体会:
在第一单元中,面向对象其实主要是找多项式、项、因子这些东西之间的关系(例如表达式由项相加、项由因子相乘等等)以及它们之间的共性(都应该有求导的方法),找到关系之后,就可以在把一个复杂的多项式求导拆分给每一个简单的因子求导,这样一层层往下寻找,最后再把求导结果一层层往上传递,就可以把一个复杂问题一步步化简成基本类 型的求导。很可惜的是一开始的时候面向对象的思考不够,导致很长时间不知道如何考虑类与类之间的关系,也导致重构时已经太晚,de不完bug了。第二单元多线程,一定要克服苦难,不怕重构,冲冲冲!



