洛谷 P9061 [Ynoi2002] Optimal Ordered Problem Solver

洛谷传送门

QOJ 传送门

考虑操作了若干次，所有点一定分布在一个自左上到右下的阶梯上或者在这个阶梯的右（上）侧。此处借用 H_W_Y 的一张图：

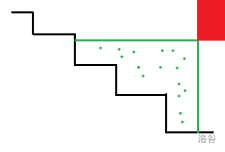
考虑如何计算答案。对于一次询问 \((X, Y)\)，如果它在阶梯左下方不用管它，否则考虑容斥，答案即为 \(x \ge X, y \ge Y\) 的点数，加上询问时不在阶梯上且 \(x \le X\) 的点数，加上询问时不在阶梯上且 \(y \le Y\) 的点数，加上阶梯上的所有点数，再加上阶梯在 \((X, Y)\) 左下方的点数。

不难发现这样计算会导致所求的被统计了 \(2\) 次，不为所求的被统计了 \(1\) 次。所以再减去总点数 \(n\) 就是答案。

发现 \(x \ge X, y \ge Y\) 的点数与时间维无关，因此是二维数点；若能处理出每个点进入阶梯的时刻（不难发现这个也是二维数点），那么询问时 \(x \le X\) 和 \(y \le Y\) 的点数也是二维数点。

剩下的问题是维护阶梯。发现阶梯上的点是随着 \(x\) 不降 \(y\) 也不增的。可以考虑直接上 FHQ Treap 维护。这样查询阶梯在 \((X, Y)\) 左下方的点数，就直接 split 出对应的部分，答案就是这部分的 size。

每次操作可能会把阶梯某一部分向右或向上挪一点。可以直接打标记维护。

还要支持在固定时刻插入一个点（前面我们已经预处理出每个点进入阶梯的时间了）。这个操作 FHQ Treap 也支持。

所以总时间复杂度是 \(O(n \log n)\)。但是因为使用 FHQ Treap 常数巨大。接下来就是卡常了。

这是一份在 QOJ 能过但在洛谷过不了的代码

// Problem: P9061 [Ynoi2002] Optimal Ordered Problem Solver
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P9061
// Memory Limit: 512 MB
// Time Limit: 4000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>
#define pb emplace_back
#define fst first
#define scd second
#define mkp make_pair
#define mems(a, x) memset((a), (x), sizeof(a))

using namespace std;
typedef long long ll;
typedef double db;
typedef unsigned long long ull;
typedef long double ldb;
typedef pair<int, int> pii;

namespace IO {
    char ibuf[1 << 20], *iS, *iT, obuf[1 << 20], *oS = obuf;
#define writesp(x) write(x), pc(' ')
#define writeln(x) write(x), pc('\n')
#define gh() (iS == iT ? iT = (iS = ibuf) + fread(ibuf, 1, 1 << 20, stdin), (iS == iT ? EOF : *iS++) : *iS++)
	template<typename T = int>
    inline T read() {
        char ch = gh();
        T x = 0;
        bool t = 0;
        while (ch < '0' || ch > '9') t |= ch == '-', ch = gh();
        while (ch >= '0' && ch <= '9') x = (x << 1) + (x << 3) + (ch ^ 48), ch = gh();
        return t ? ~(x - 1) : x;
    }
    inline void flush () {
    	fwrite(obuf, 1, oS - obuf, stdout), oS = obuf;
	}
    inline void pc (char ch) {
    	if (oS == obuf + (1 << 20)) flush(); 
    	*oS++ = ch;
	}
	template<typename _Tp>
    inline void write (_Tp x) {
    	static char stk[64], *tp = stk;
    	if (x < 0) x = ~(x - 1), pc('-');
		do *tp++ = x % 10, x /= 10;
		while (x);
		while (tp != stk) pc((*--tp) | 48);
    }
}

using IO::read;
using IO::write;
using IO::pc;
using IO::flush;

const int maxn = 1000100;

int n, m, ans[maxn], head[maxn], len, val[maxn], nxt[maxn];
pii a[maxn];
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());

inline void add(int x, int y) {
	val[++len] = y;
	nxt[len] = head[x];
	head[x] = len;
}

struct node {
	int o, x, y, qx, qy, id;
} qq[maxn];

struct {
	int c[maxn];
	
	inline void init() {
		mems(c, 0);
	}
	
	inline void update(int x, int d) {
		for (int i = x; i <= n; i += (i & (-i))) {
			c[i] += d;
		}
	}
	
	inline int query(int x) {
		int res = 0;
		for (int i = x; i; i -= (i & (-i))) {
			res += c[i];
		}
		return res;
	}
} t1, t2;

struct {
	int c[maxn];
	
	inline void init() {
		mems(c, 0x3f);
	}
	
	inline void update(int x, int d) {
		for (int i = x; i; i -= (i & (-i))) {
			c[i] = min(c[i], d);
		}
	}
	
	inline int query(int x) {
		int res = 2e9;
		for (int i = x; i <= n; i += (i & (-i))) {
			res = min(res, c[i]);
		}
		return res;
	}
} t3;

struct {
	int c[maxn];
	
	inline void init() {
		mems(c, -0x3f);
	}
	
	inline void update(int x, int d) {
		for (int i = x; i; i -= (i & (-i))) {
			c[i] = max(c[i], d);
		}
	}
	
	inline int query(int x) {
		int res = -2e9;
		for (int i = x; i <= n; i += (i & (-i))) {
			res = max(res, c[i]);
		}
		return res;
	}
} t4;

int rt, nt;

struct wwh {
	int p, ls, rs, x, y, sz, tx, ty;
} b[maxn];

inline void pushup(int x) {
	b[x].sz = b[b[x].ls].sz + b[b[x].rs].sz + 1;
}

inline void pushdown(int x) {
	int &tx = b[x].tx, &ty = b[x].ty, l = b[x].ls, r = b[x].rs;
	wwh &L = b[l], &R = b[r];
	if (tx != -1) {
		if (l) {
			L.x = L.tx = tx;
		}
		if (r) {
			R.x = R.tx = tx;
		}
		tx = -1;
	}
	if (ty != -1) {
		if (l) {
			L.y = L.ty = ty;
		}
		if (r) {
			R.y = R.ty = ty;
		}
		ty = -1;
	}
}

// x <= k, x > k
void splitx(int u, int k, int &x, int &y) {
	if (!u) {
		x = y = 0;
		return;
	}
	pushdown(u);
	if (b[u].x <= k) {
		x = u;
		splitx(b[u].rs, k, b[u].rs, y);
	} else {
		y = u;
		splitx(b[u].ls, k, x, b[u].ls);
	}
	pushup(u);
}

// y > k, y <= k
void splity(int u, int k, int &x, int &y) {
	if (!u) {
		x = y = 0;
		return;
	}
	pushdown(u);
	if (b[u].y > k) {
		x = u;
		splity(b[u].rs, k, b[u].rs, y);
	} else {
		y = u;
		splity(b[u].ls, k, x, b[u].ls);
	}
	pushup(u);
}

// x <= kx, y >= ky
void split(int u, int kx, int ky, int &x, int &y) {
	if (!u) {
		x = y = 0;
		return;
	}
	pushdown(u);
	if (b[u].x < kx || (b[u].x == kx && b[u].y >= ky)) {
		x = u;
		split(b[u].rs, kx, ky, b[u].rs, y);
	} else {
		y = u;
		split(b[u].ls, kx, ky, x, b[u].ls);
	}
	pushup(u);
}

int merge(int x, int y) {
	if (!x || !y) {
		return x | y;
	}
	if (b[x].p < b[y].p) {
		pushdown(x);
		b[x].rs = merge(b[x].rs, y);
		pushup(x);
		return x;
	} else {
		pushdown(y);
		b[y].ls = merge(x, b[y].ls);
		pushup(y);
		return y;
	}
}

inline int newnode(int x, int y) {
	int u = ++nt;
	b[u].x = x;
	b[u].y = y;
	b[u].sz = 1;
	b[u].p = rnd();
	b[u].tx = b[u].ty = -1;
	return u;
}

void solve() {
	n = read();
	m = read();
	for (int i = 1; i <= n; ++i) {
		a[i].fst = read();
		a[i].scd = read();
	}
	sort(a + 1, a + n + 1);
	// for (int i = 1; i <= n; ++i) {
		// printf("x, y: %d %d\n", a[i].fst, a[i].scd);
	// }
	for (int i = 1; i <= m; ++i) {
		qq[i].o = read();
		qq[i].x = read();
		qq[i].y = read();
		qq[i].qx = read();
		qq[i].qy = read();
		qq[i].id = i;
	}
	t3.init();
	t4.init();
	sort(qq + 1, qq + m + 1, [&](const node &a, const node &b) {
		return a.qx > b.qx;
	});
	for (int i = 1, j = n; i <= m; ++i) {
		while (j && a[j].fst > qq[i].qx) {
			t1.update(a[j].scd, 1);
			--j;
		}
		ans[qq[i].id] = n - j - t1.query(qq[i].qy);
	}
	sort(qq + 1, qq + m + 1, [&](const node &a, const node &b) {
		return a.x > b.x;
	});
	t1.init();
	for (int i = n, j = 1; i; --i) {
		t1.update(a[i].fst, 1);
		t2.update(a[i].scd, 1);
		while (j <= m && qq[j].x >= a[i].fst) {
			t3.update(qq[j].y, qq[j].id);
			++j;
		}
		int t = t3.query(a[i].scd);
		if (t <= m) {
			// printf("i: %d %d\n", i, t);
			add(t, i);
		}
	}
	sort(qq + 1, qq + m + 1, [&](const node &a, const node &b) {
		return a.id < b.id;
	});
	for (int i = 1, x, y, z; i <= m; ++i) {
		if (t4.query(qq[i].x + 1) <= qq[i].y) {
			t4.update(qq[i].x, qq[i].y);
			splitx(rt, qq[i].x, x, z);
			splity(x, qq[i].y, x, y);
			if (y) {
				if (qq[i].o == 1) {
					b[y].y = b[y].ty = qq[i].y;
				} else {
					b[y].x = b[y].tx = qq[i].x;
				}
			}
			rt = merge(merge(x, y), z);
		}
		for (int _ = head[i]; _; _ = nxt[_]) {
			int j = val[_];
			int xx = a[j].fst, yy = a[j].scd;
			t1.update(xx, -1);
			t2.update(yy, -1);
			if (qq[i].o == 1) {
				yy = qq[i].y;
			} else {
				xx = qq[i].x;
			}
			split(rt, xx, yy, x, y);
			rt = merge(merge(x, newnode(xx, yy)), y);
		}
		if (t4.query(qq[i].qx + 1) > qq[i].qy) {
			ans[i] = 0;
		} else {
			ans[i] += t1.query(qq[i].qx) + t2.query(qq[i].qy) + b[rt].sz;
			splitx(rt, qq[i].qx, x, z);
			splity(x, qq[i].qy, x, y);
			// printf("sz[%d] = %d\n", y, b[y].sz);
			ans[i] += b[y].sz - n;
			rt = merge(merge(x, y), z);
		}
		writeln(ans[i]);
	}
}

int main() {
	int T = 1;
	// scanf("%d", &T);
	while (T--) {
		solve();
	}
	flush();
	return 0;
}

这是一份在洛谷能过的代码

// Problem: P9061 [Ynoi2002] Optimal Ordered Problem Solver
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P9061
// Memory Limit: 512 MB
// Time Limit: 4000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>
#define pb emplace_back
#define fst first
#define scd second
#define mkp make_pair
#define mems(a, x) memset((a), (x), sizeof(a))

using namespace std;
typedef long long ll;
typedef unsigned uint;
typedef double db;
typedef unsigned long long ull;
typedef long double ldb;
typedef pair<uint, uint> pii;

namespace IO {
    char ibuf[1 << 20], *iS, *iT, obuf[1 << 20], *oS = obuf;
#define writesp(x) write(x), pc(' ')
#define writeln(x) write(x), pc('\n')
#define gh() (iS == iT ? iT = (iS = ibuf) + fread(ibuf, 1, 1 << 20, stdin), (iS == iT ? EOF : *iS++) : *iS++)
	template<typename T = uint>
    inline T read() {
        char ch = gh();
        T x = 0;
        bool t = 0;
        while (ch < '0' || ch > '9') t |= ch == '-', ch = gh();
        while (ch >= '0' && ch <= '9') x = (x << 1) + (x << 3) + (ch ^ 48), ch = gh();
        return t ? ~(x - 1) : x;
    }
    inline void flush () {
    	fwrite(obuf, 1, oS - obuf, stdout), oS = obuf;
	}
    inline void pc (char ch) {
    	if (oS == obuf + (1 << 20)) flush(); 
    	*oS++ = ch;
	}
	template<typename _Tp>
    inline void write (_Tp x) {
    	static char stk[64], *tp = stk;
    	if (x < 0) x = ~(x - 1), pc('-');
		do *tp++ = x % 10, x /= 10;
		while (x);
		while (tp != stk) pc((*--tp) | 48);
    }
}

using IO::read;
using IO::write;
using IO::pc;
using IO::flush;

const uint maxn = 1000100;

uint n, m, ans[maxn], head[maxn], len, val[maxn], nxt[maxn];
pii a[maxn], c[maxn];
mt19937 rnd(time(NULL));

inline void add(uint x, uint y) {
	val[++len] = y;
	nxt[len] = head[x];
	head[x] = len;
}

struct node {
	uint o, x, y, qx, qy, id;
} qq[maxn], pp[maxn];

struct {
	uint c[maxn];
	
	inline void init() {
		mems(c, 0);
	}
	
	inline void update(const uint &x, const uint &d) {
		for (uint i = x; i <= n; i += (i & (-i))) {
			c[i] += d;
		}
	}
	
	inline uint query(const uint &x) {
		uint res = 0;
		for (uint i = x; i; i -= (i & (-i))) {
			res += c[i];
		}
		return res;
	}
} t1, t2;

struct {
	uint c[maxn];
	
	inline void init() {
		mems(c, 0x3f);
	}
	
	inline void update(const uint &x, const uint &d) {
		for (uint i = x; i; i -= (i & (-i))) {
			(c[i] > d ? c[i] = d : 0);
		}
	}
	
	inline uint query(const uint &x) {
		uint res = 2e9;
		for (uint i = x; i <= n; i += (i & (-i))) {
			(res > c[i] ? res = c[i] : 0);
		}
		return res;
	}
} t3;

struct {
	uint c[maxn];
	
	inline void update(const uint &x, const uint &d) {
		for (uint i = x; i; i -= (i & (-i))) {
			(c[i] < d ? c[i] = d : 0);
		}
	}
	
	inline uint query(const uint &x) {
		uint res = 0;
		for (uint i = x; i <= n; i += (i & (-i))) {
			(res < c[i] ? res = c[i] : 0);
		}
		return res;
	}
} t4;

uint rt, nt;

struct wwh {
	uint p, ls, rs, x, y, sz, tx, ty;
} b[maxn];

// x <= k, x > k
void splitx(uint u, const uint &k, uint &x, uint &y) {
	if (!u) {
		x = y = 0;
		return;
	}
	wwh &t = b[u];
	uint &tx = t.tx, &ty = t.ty, &l = t.ls, &r = t.rs;
	wwh &L = b[l], &R = b[r];
	if (tx) {
		if (l) {
			L.x = L.tx = tx;
		}
		if (r) {
			R.x = R.tx = tx;
		}
		tx = 0;
	}
	if (ty) {
		if (l) {
			L.y = L.ty = ty;
		}
		if (r) {
			R.y = R.ty = ty;
		}
		ty = 0;
	}
	if (t.x <= k) {
		x = u;
		splitx(t.rs, k, t.rs, y);
	} else {
		y = u;
		splitx(t.ls, k, x, t.ls);
	}
	t.sz = b[l].sz + b[r].sz + 1;
}

// y > k, y <= k
void splity(uint u, const uint &k, uint &x, uint &y) {
	if (!u) {
		x = y = 0;
		return;
	}
	wwh &t = b[u];
	uint &tx = t.tx, &ty = t.ty, &l = t.ls, &r = t.rs;
	wwh &L = b[l], &R = b[r];
	if (tx) {
		if (l) {
			L.x = L.tx = tx;
		}
		if (r) {
			R.x = R.tx = tx;
		}
		tx = 0;
	}
	if (ty) {
		if (l) {
			L.y = L.ty = ty;
		}
		if (r) {
			R.y = R.ty = ty;
		}
		ty = 0;
	}
	if (t.y > k) {
		x = u;
		splity(t.rs, k, t.rs, y);
	} else {
		y = u;
		splity(t.ls, k, x, t.ls);
	}
	t.sz = b[l].sz + b[r].sz + 1;
}

// x <= kx, y >= ky
void split(uint u, const uint &kx, const uint &ky, uint &x, uint &y) {
	if (!u) {
		x = y = 0;
		return;
	}
	wwh &t = b[u];
	uint &tx = t.tx, &ty = t.ty, &l = t.ls, &r = t.rs;
	wwh &L = b[l], &R = b[r];
	if (tx) {
		if (l) {
			L.x = L.tx = tx;
		}
		if (r) {
			R.x = R.tx = tx;
		}
		tx = 0;
	}
	if (ty) {
		if (l) {
			L.y = L.ty = ty;
		}
		if (r) {
			R.y = R.ty = ty;
		}
		ty = 0;
	}
	if (t.x < kx || (t.x == kx && t.y >= ky)) {
		x = u;
		split(t.rs, kx, ky, t.rs, y);
	} else {
		y = u;
		split(t.ls, kx, ky, x, t.ls);
	}
	t.sz = b[l].sz + b[r].sz + 1;
}

uint merge(const uint &x, const uint &y) {
	if (!x || !y) {
		return x | y;
	}
	if (b[x].p < b[y].p) {
		wwh &t = b[x];
		uint &tx = t.tx, &ty = t.ty, &l = t.ls, &r = t.rs;
		wwh &L = b[l], &R = b[r];
		if (tx) {
			if (l) {
				L.x = L.tx = tx;
			}
			if (r) {
				R.x = R.tx = tx;
			}
			tx = 0;
		}
		if (ty) {
			if (l) {
				L.y = L.ty = ty;
			}
			if (r) {
				R.y = R.ty = ty;
			}
			ty = 0;
		}
		t.rs = merge(t.rs, y);
		t.sz = b[l].sz + b[r].sz + 1;
		return x;
	} else {
		wwh &t = b[y];
		uint &tx = t.tx, &ty = t.ty, &l = t.ls, &r = t.rs;
		wwh &L = b[l], &R = b[r];
		if (tx) {
			if (l) {
				L.x = L.tx = tx;
			}
			if (r) {
				R.x = R.tx = tx;
			}
			tx = 0;
		}
		if (ty) {
			if (l) {
				L.y = L.ty = ty;
			}
			if (r) {
				R.y = R.ty = ty;
			}
			ty = 0;
		}
		t.ls = merge(x, t.ls);
		t.sz = b[l].sz + b[r].sz + 1;
		return y;
	}
}

inline uint newnode(const uint &x, const uint &y) {
	uint u = ++nt;
	b[u].x = x;
	b[u].y = y;
	b[u].sz = 1;
	b[u].p = rnd();
	return u;
}

void solve() {
	n = read();
	m = read();
	for (uint i = 1; i <= n; ++i) {
		a[i].fst = read();
		a[i].scd = read();
		add(a[i].fst, i);
		c[i] = a[i];
	}
	uint tot = 0;
	for (uint i = 1; i <= n; ++i) {
		for (uint _ = head[i]; _; _ = nxt[_]) {
			a[++tot] = c[val[_]];
		}
	}
	for (uint i = 1; i <= m; ++i) {
		qq[i].o = read();
		qq[i].x = read();
		qq[i].y = read();
		qq[i].qx = read();
		qq[i].qy = read();
		qq[i].id = i;
	}
	t3.init();
	len = 0;
	mems(head, 0);
	for (uint i = 1; i <= m; ++i) {
		pp[i] = qq[i];
		add(qq[i].qx, i);
	}
	tot = 0;
	for (uint i = n; i; --i) {
		for (uint _ = head[i]; _; _ = nxt[_]) {
			qq[++tot] = pp[val[_]];
		}
	}
	for (uint i = 1, j = n; i <= m; ++i) {
		while (j && a[j].fst > qq[i].qx) {
			t1.update(a[j].scd, 1);
			--j;
		}
		ans[qq[i].id] = n - j - t1.query(qq[i].qy);
	}
	len = 0;
	mems(head, 0);
	for (uint i = 1; i <= m; ++i) {
		pp[i] = qq[i];
		add(qq[i].x, i);
	}
	tot = 0;
	for (uint i = n; i; --i) {
		for (uint _ = head[i]; _; _ = nxt[_]) {
			qq[++tot] = pp[val[_]];
		}
	}
	len = 0;
	mems(head, 0);
	t1.init();
	for (uint i = n, j = 1; i; --i) {
		t1.update(a[i].fst, 1);
		t2.update(a[i].scd, 1);
		while (j <= m && qq[j].x >= a[i].fst) {
			t3.update(qq[j].y, qq[j].id);
			++j;
		}
		uint t = t3.query(a[i].scd);
		if (t <= m) {
			// printf("i: %d %d\n", i, t);
			add(t, i);
		}
	}
	for (uint i = 1; i <= m; ++i) {
		pp[qq[i].id] = qq[i];
	}
	for (uint i = 1; i <= m; ++i) {
		qq[i] = pp[i];
	}
	for (uint i = 1, x, y, z, X, Y; i <= m; ++i) {
		t4.update(qq[i].x, qq[i].y);
		splity(rt, qq[i].y, x, z);
		splitx(z, qq[i].x, y, z);
		if (y) {
			if (qq[i].o == 1) {
				b[y].y = b[y].ty = qq[i].y;
			} else {
				b[y].x = b[y].tx = qq[i].x;
			}
		}
		for (uint _ = head[i]; _; _ = nxt[_]) {
			uint j = val[_];
			uint xx = a[j].fst, yy = a[j].scd;
			t1.update(xx, -1);
			t2.update(yy, -1);
			if (qq[i].o == 1) {
				yy = qq[i].y;
			} else {
				xx = qq[i].x;
			}
			split(y, xx, yy, X, Y);
			y = merge(merge(X, newnode(xx, yy)), Y);
			// y = merge(X, merge(newnode(xx, yy), Y));
		}
		// rt = merge(merge(x, y), z);
		rt = merge(x, merge(y, z));
		if (t4.query(qq[i].qx + 1) > qq[i].qy) {
			ans[i] = 0;
		} else {
			ans[i] += t1.query(qq[i].qx) + t2.query(qq[i].qy) + b[rt].sz;
			splity(rt, qq[i].qy, x, z);
			splitx(z, qq[i].qx, y, z);
			// printf("sz[%d] = %d\n", y, b[y].sz);
			ans[i] += b[y].sz - n;
			// rt = merge(merge(x, y), z);
			rt = merge(x, merge(y, z));
		}
		writeln(ans[i]);
	}
}

int main() {
	int T = 1;
	// scanf("%d", &T);
	while (T--) {
		solve();
	}
	flush();
	return 0;
}