2024.1 做题记录
27. CF1916F Group Division
考虑增量构造第一个集合。首先令 \(S = \{1\}\)，然后不断找到下一个点 \(u\)，使得它在抠掉 \(S\) 的图上不是割点，并且与 \(S\) 连通。然后令 \(S \gets S \cup \{u\}\)。
可以证明一定能找到这样的 \(u\)。
因为对于抠掉 \(S\) 的新图上，若存在割点 \(v\)，那么删除 \(v\) 后的每一个连通块都与 \(S\) 连通，否则与题目原图没有割点的条件矛盾。
所以我们能找到一个割点 \(w\) 使得 dfs 树上它存在一棵子树没有割点。由上一定能在这棵子树找到一个与 \(S\) 连通的点。
综上所述一定能找到这样的 \(u\)。
时间复杂度 \(O(n(n + m))\)。
28. P9061 [Ynoi2002] Optimal Ordered Problem Solver
考虑操作了若干次，所有点一定分布在一个自左上到右下的阶梯上或者在这个阶梯的右（上）侧。此处借用 H_W_Y 的一张图：
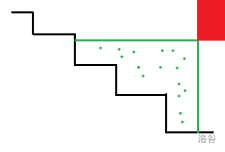
考虑如何计算答案。对于一次询问 \((X, Y)\)，如果它在阶梯左下方不用管它，否则考虑容斥，答案即为 \(x \ge X, y \ge Y\) 的点数，加上询问时不在阶梯上且 \(x \le X\) 的点数，加上询问时不在阶梯上且 \(y \le Y\) 的点数，加上阶梯上的所有点数，再加上阶梯在 \((X, Y)\) 左下方的点数。
不难发现这样计算会导致所求的被统计了 \(2\) 次，不为所求的被统计了 \(1\) 次。所以再减去总点数 \(n\) 就是答案。
发现 \(x \ge X, y \ge Y\) 的点数与时间维无关，因此是二维数点；若能处理出每个点进入阶梯的时刻（不难发现这个也是二维数点），那么询问时 \(x \le X\) 和 \(y \le Y\) 的点数也是二维数点。
剩下的问题是维护阶梯。发现阶梯上的点是随着 \(x\) 不降 \(y\) 也不增的。可以考虑直接上 FHQ Treap 维护。这样查询阶梯在 \((X, Y)\) 左下方的点数，就直接 split 出对应的部分，答案就是这部分的 size。
每次操作可能会把阶梯某一部分向右或向上挪一点。可以直接打标记维护。
还要支持在固定时刻插入一个点（前面我们已经预处理出每个点进入阶梯的时间了）。这个操作 FHQ Treap 也支持。
所以总时间复杂度是 \(O(n \log n)\)。但是因为使用 FHQ Treap 常数巨大。接下来就是卡常了。
29. CF1234F Yet Another Substring Reverse
搞笑题，显然相当于选两个子串拼起来，子串长度显然不会超过 \(|\Sigma|\)，子集取一下长度 \(\max\) 就行了。
30. CF744C Hongcow Buys a Deck of Cards
实际上是一个二维可行性背包，把其中一维塞进状态值里面即可。
31. P4094 [HEOI2016/TJOI2016] 字符串
二分答案，倍增跳到这个子串对应的结点。线段树合并维护 \(\text{endpos}\) 集合即可。
32. CF1037H Security
贪心的从后往前加最小的字符即可。跳到 SAM 对应的结点位置，判一下子串位置即可。可以使用线段树合并维护 \(\text{endpos}\) 集合。
33. P6292 区间本质不同子串个数 & UVA13023 Text Processor
考虑类比区间数颜色。扫描线扫询问的 \(r = i\)，然后对于一个 \(i\) 的后缀 \(S[j : i]\)，我们把它上一次出现时的左端点位置 \(-1\)，现在的左端点位置（即 \(j\)）\(+1\)。那么查询就是 \([l, r]\) 的区间和。
考虑把 SAM 建出来。设 \(S[1 : i]\) 对应的点为 \(a_i\)。那么相当于我们对于每个点维护一个颜色 \(b_u\) 表示这个等价类上一次出现的右端点，每次把 parent tree 上 \(a_i\) 到根的点拎出来做一次操作。设点 \(u\) 的长度区间为 \([l_u, r_u]\)，那么一次操作相当于把 \([b_u - r_u + 1, b_u - l_u + 1]\) 的位置 \(-1\)。最后把 \([1, i]\) \(+1\)。
剩下的部分是 P9340 [JOISC 2023 Day3] Tourism。考虑树剖后把树拍到 dfs 序上，每次推平 \(O(\log n)\) 个区间。
但是事实上因为我们每次只是对一条重链前缀赋值，所以不用真的去实现一个 ODT。每条重链分别维护一些从浅到深的连续段即可。
总时间复杂度为 \(O(n \log^2 n + m \log n)\)。
34. P5576 [CmdOI2019] 口头禅
这个题感觉很牛逼。
考虑建广义 SAM，然后给第 \(i\) 个串经过的所有点染上颜色 \(i\)。我们维护每个点子树内的颜色连续段，表示出现过 \([l, r]\) 的颜色。
考虑按 SAM 的 \(\text{len}\) 从大到小启发式合并并找新产生的 \([l, r]\) 能贡献到哪些询问。显然能贡献到完全被它包含的询问。并且由于我们是按 \(\text{len}\) 从大到小考虑的，所以贡献完后立刻删除这个询问就行。所以我们可以暴力找，暴力更新。
35. CF733F Drivers Dissatisfaction
显然分在或不在最小生成树上讨论。
在是简单的。不在，只会新加一条边，然后抠掉最小生成树上两点路径的最大边。随便维护一下即可。
36. P4770 [NOI2018] 你的名字
统计 \(T\) 的本质不同子串数减去在 \(S_{l \sim r}\) 中的子串。
对每个 \(i\) 求出 \(f_i\) 表示 \(T_{1 \sim i}, T_{2 \sim i}, \cdots, T_{f_i \sim i}\) 是新产生的子串（显然其为插入 \(T_i\) 后后缀自动机的 \(\text{lst}\) 的 \(\text{link}\) 的 \(\text{len}\)）。
然后我们把 \(T\) 放到 \(S\) 匹配。如果有出边并且出边的 \(\text{endpos}\) 集合包含对应的位置就可以把匹配长度 \(+1\)。否则匹配长度 \(-1\)（注意不跳 \(\text{link}\)），因为减小匹配长度可能能匹配。如果匹配长度等于 \(\text{len}({\text{link}(u)})\) 那么长度就超出 \(u\) 的范围了，就要 \(u \gets \text{link}(u)\)。
37. CF666E Forensic Examination
建广义 SAM，预处理出 \(S\) 的每个前缀在广义 SAM 上的最长匹配后缀。那么找 \(S_{pl \sim pr}\) 对应的子串直接倍增跳就行。
线段树合并处理一下在哪个子串出现的信息即可。
38. P5161 WD与数列
考虑两个 \(\text{lcs}\) 为 \(t\) 的前缀 \([1, i]\) 和 \([1, j]\)。我们发现可能的左端点取值为 \(\min(|i - j| - 1, t)\)。
考虑建出 SAM。那么两点的 \(\text{lca}\) 的 \(\text{len}\) 就是它们的 \(\text{lcs}\)。枚举这个 \(\text{lca}\)。那么相当于先考虑一棵子树的所有 \(\text{endpos}\) 与之前的产生的贡献，然后再加入这棵子树的 \(\text{endpos}\)。
可以使用线段树合并 + 启发式合并或 DSU on tree + BIT。不难发现两个 \(\text{endpos}\) 的贡献即上文的 \(\min(|i - j| - 1, t)\) 是分段一次函数形式。线段树维护 \(\text{endpos}\) 和及个数即可。
时间复杂度 \(O(n \log^2 n)\)，空间复杂度 \(O(n \log n)\)。
39. CF1919E Counting Prefixes
考虑一个很类似的题。我们把正数和负数分开来考虑，最后用 \(0\) 连接一些连续段，形如 \(0 - \text{正} - 0 - \text{正} - 0 - \text{负}\)。
先考虑正数。设 \(f_{i, j}\) 为考虑了 \(\ge i\) 的正数，形成了 \(j\) 个连续段的方案数。设 \(i\) 的出现次数为 \(c_i\)。
那么之前的每个段两端都需要接一个 \(i\) 下来，两段之间也可以只用一个 \(i\) 连接。
特别地，如果已经考虑到了结尾位置 \(n\)，右端不用接数。于是我们状态再记一个 \(f_{i, j, 0/1}\) 表示包含位置 \(n\) 的段是否出现。
那么对于 \(f_{i + 1, j, 0}\) 的转移，新的段数 \(k = c_i - j\) 可以直接被计算出来。转移系数是 \(c_i\) 个数分配给 \(j + 1\) 个空的插板。我们有：
对于 \(f_{i + 1, j, 1}\) 的转移，新的段数为 \(k = c_i - j + 1\)。有转移：
同样地考虑负数，设 \(g_{i, j}\) 为考虑了 \(\le -i\) 的负数，形成了 \(j\) 个连续段的方案数。转移类似。
计算答案，只用枚举正数的段数 \(i\)，如果 \(0\) 不为 \(n\) 的前缀和，那么负数的段数为 \(c_0 - i\)，否则为 \(c_0 - i - 1\)。讨论一下 \(n\) 的前缀和是给 \(0\)，正数还是负数，再乘上给段选择位置的系数。所以：
直接计算 \(f, g\) 复杂度为 \(O(n^2)\)。但是注意到 \(f, g\) 初值只有 \(O(1)\) 个位置有值，每次转移一个位置会转移到固定的另一个位置，最后一维只会进行 \(0 \to 1\) 的转移不会进行 \(1 \to 0\) 的转移。所以 dp 数组每行有值的位置数是 \(\color{red}{O(1)}\) 的。如果我们用 unordered_map 把有值的位置存下来，复杂度将是 \(\color{red}{O(n)}\)。
40. CF1919F2 Wine Factory (Hard Version)
题目看着感觉很像最大流，不妨建模，\(S \to i\)，容量为 \(a_i\)；\(i \to T\)，容量为 \(b_i\)；\(i \to i + 1\)，容量为 \(c_i\)。答案是这个图的最大流。
考虑最大流转最小割。观察到 \(S \to i\) 和 \(i \to T\) 的边恰好被割掉一条。因为不可能都不被割，\(S, T\) 不能同时和 \(i\) 连通。如果 \(S, i\) 连通就割 \(i \to T\)，否则割 \(S \to i\)。
这样如果割了 \(i \to T\) 和 \(S \to i + 1\)，也要割掉 \(i \to i + 1\) 的边。所以实际上是一个动态 dp。
考虑线段树维护，\([l, r]\) 对应的结点维护 \(f_{0/1, 0/1}\) 表示当 \(l\) 是割到 \(S\) 还是到 \(T\) 的边，\(r\) 是割到 \(S\) 还是到 \(T\) 的边的边权最小值。那么合并两儿子时如果是 \(f_{\ast, 1}\) 和 \(f_{0, \ast}\) 合并，那么费用再加 \(c_{mid}\)。
时间复杂度 \(O(n + m \log n)\)。
41. CF727F Polycarp's problems
考虑用前面的正数去抵消后面绝对值尽量小的负数。这样能保证删去的是尽量大的。
处理完一遍后可能还会剩下若干负数。询问时在这些负数的前缀和数组上二分即可。
42. P4112 [HEOI2015] 最短不公共子串
每个串分别建后缀自动机和子序列自动机，bfs 即可。
43. CF1073G Yet Another LCP Problem & P7409 SvT
考虑对反串建 SAM，设 \([i, n]\) 的后缀对应 SAM 的点是 \(a_i\)。
那么 \(\text{lcp}(s[i : n], s[j : n]) = \text{len}(\text{lca}(a_i, a_j))\)。
于是问题变成了，给定一些点，统计两两 \(\text{lca}\) 点权之和。
考虑建虚树，枚举每个点 \(u\) 作为 \(\text{lca}\) 的次数。设当前已经考虑过的儿子的 \(sz\) 之和为 \(s\)，那么 \(v\) 作为子树会有 \(s \times sz_v\) 次数的贡献。再乘上 \(len_u\) 累加进答案即可。
若使用 dfs 序 LCA，时间复杂度 \(O((n + m) \log n)\)。
44. CF1379E Inverse Genealogy
\(n\) 为偶数显然无解。
否则我们可以构造一棵 \(n\) 个点的完全二叉树，当 \(n + 1\) 是 \(2\) 的幂时满足 \(m = 0\)，否则 \(m = 1\)。
当 \(n \ge 5\) 时可以递归至 \((n - 2, m - 1)\)，再挂一个叶子即可。
但是可能会出现 \(n + 1\) 是 \(2\) 的幂，但 \(n - 1\) 不是，可能会把有解判成无解。
打一个补丁，如果上面那种情况递归下去无解，当 \(n \ge 11\) 时我们可以接一棵 \(3\) 个点的满二叉树，然后再递归至 \((n - 4, m - 1)\)。
时间复杂度 \(O(n)\)。
45. CF1383D Rearrange
考虑从大到小填数。如果这个数是行或列最大值就给它新开一行或一列。同时用队列维护一些还没填的位置。对于一个行最大值 \((x, y)\)，因为要求双调，把 \((x, y - 1), (x, y - 2), \ldots, (x, 1)\) 依次塞入队列即可。列最大值同理。
46. CF1444D Rectangular Polyline
显然我们需要把两个集合 \(X, Y\) 分成 \(X^+, X^-, Y^+, Y^-\)。
不妨设 \(|X^+| \le |Y^+|\)。考虑把 \(X^-, X^+\) 从大到小排序，\(Y^-, Y^+\) 从小到大排序。依次向右上，左上，左下走。因为右上和坐下的折线不会越过一条固定的直线，所以不会相交。
寻找划分方案用 bitset 优化可行性背包，复杂度 \(O(\frac{n^2V}{\omega})\)。
47. CF1237H Balanced Reversals
容易想到把 \(s, t\) 分成长度为 \(2\) 的段考虑。容易发现 \(00, 11\) 的个数在操作过程中不会改变，所以若两串的 \(00\) 或 \(11\) 个数不相等则无解。
考虑依次对 \(i = 2, 4, \ldots, n\) 构造 \(s[1 : i] = t[n - i + 1 : n]\)。对于 \(s_{j - 1}s_j = yx\)，依次操作 \(j - 2, j\) 可以把 \(s\) 变成 \(xy s_1 s_2 \ldots s_{j - 2}\)。
但是上面的方法只在 \(s\) 的 \(01\) 数量等于 \(t\) 的 \(10\) 数量有效。设 \(f(s)\) 为 \(s\) 的 \(01\) 数量减 \(10\) 数量的值，我们的目标是让 \(f(s) = -f(t)\)。那么若 \(|f(s)| \ge |f(t)|\)，一定可以找到 \(s\) 的一个前缀，使得翻转它后 \(f(s) = -f(t)\)。因为 \(f(s)\) 对于 \(s\) 的每个前缀一定 \(+1, -1\) 或不变，因此 \(0 \sim |f(s)|\) 的每个数（或其相反数）都能经过。若 \(|f(s)| < |f(t)|\)，反过来，一定可以找到 \(t\) 的一个前缀，使得翻转它后 \(f(s) = -f(t)\)。可以全部操作完后再翻转达到翻转 \(t\) 的前缀的效果。
操作次数为 \(n + 1\)。时间复杂度 \(O(n^2)\)。
48. CF1329D Dreamoon Likes Strings
考虑构造一个新串 \(t\)，只保留原串 \(s_{i - 1} = s_i\) 的字符 \(s_i\)。设 \(a_i\) 为 \(t_i\) 在原串的位置。
那么新串上我们有两种操作：
- \(\forall i\)，删除 \(t_i\)（相当于删除原串中的 \([a_i, a_i]\)）；
- \(\forall t_i \ne t_{i + 1}\)，删除 \(t_i, t_{i + 1}\)（相当于删除原串中的 \([a_i, a_{i + 1} - 1]\)）。
设 \(t\) 中字符 \(i\) 出现了 \(c_i\) 次，出现次数最多的字符为 \(p\)。
若 \(2c_p \ge |t|\)，我们可以不断将 \(p\) 与其他字符配对，最后剩下一些 \(p\) 逐个删除即可。
若 \(2c_p < |t|\)，我们可以先随意让一些字符配对，若删到某一步发现存在 \(2c_p \ge |t|\) 了就换上面的做法。
实现时这部分可以用栈。
注意因为我们要还原串的下标，因此使用线段树每个字符是否还没被删。每次删除一段相当于区间赋值。
时间复杂度 \(O(n (\log n + |\Sigma|))\)。
49. CF1396E Distance Matching
好题。
考虑每条边两端的子树大小 \(a, b\)。显然答案下界 \(L = \sum a \bmod 2\)，上界 \(R = \sum \min(a, b)\)。并且 \(k\) 的奇偶性已确定。
然后考虑距离的式子 \(dep_x + dep_y - 2dep_{\text{lca}(x, y)}\)。因为一条经过重心的路径的 \(dep_{\text{lca}(x, y)} = 0\)，我们只要调整一些点对的 \(dep_{\text{lca}(x, y)}\) 即可。
设当前还要调整的距离 \(r = R - m\)。每次我们拿出最大的子树 \(x\) 中最深的非叶子结点 \(y\)。然后把 \(y\) 的儿子和 \(y\) 拿出两个匹配（优先拿 \(y\) 的儿子），然后删掉。因为我们每次时从最大的子树内删两个点，所以重心不会移动。
如果某刻 \(2dep_y > r\) 了，那么我们需要拿 \(x\) 子树内深度为 \(\frac{r}{2}\) 的点，在它的儿子里面找匹配，然后立刻退出循环。
最后我们把还没被考虑过的点的 dfs 序拿出来，第 \(i\) 个点匹配第 \(i + \frac{len}{2}\) 个点即可。
50. CF1793E Velepin and Marketing
考虑把 \(a_i\) 从小到大排序，那么进入答案的 \(a\) 一定是一段前缀，我们可以 dp 出 \(f_i\) 表示 \([1, i]\) 的人都进入答案的最大划分段数。注意若 \(i < a_i\) 则要考虑让前 \(a_i\) 个人成一段的方案。
然后预处理每个 \(k\) 的回答即可。
51. P8098 [USACO22JAN] Tests for Haybales G
考虑连边 \(j_i + 1 \to i\)，那么形成了一棵树。发现从上到下前一层大概比后一层大 \(K\)。我们令 \(x_i = (n - dep_i) K + y_i\)。那么 \(y_i\) 需要满足它小于它的所有儿子，并且同层按编号排序后 \(y_i\) 小于所有在它后面的点。考虑 \(y_i\) 取 \(-dfn_i\) 即满足条件。
52. CF1667C Half Queen Cover
考虑用 \(k\) 个棋子覆盖 \(k\) 行 \(k\) 列，剩下 \((n - k) \times (n - k)\) 的正方形用之前能覆盖到的棋子斜着覆盖。二分求出最小的这样的 \(k\)。
然后就变成了求出排列 \(p\) 满足 \(i - p_i \in \{-\frac{n - 1}{2}, -\frac{n - 1}{2} + 1, \ldots, \frac{n - 1}{2}\}\)。交替取即可。
53. CF1905F Field Should Not Be Empty
好蠢啊。
我们称 \(i\) 差点有贡献当且仅当它前面恰好有一个点比它大，后面恰好有一个点比它小。
那么交换 \(i, j\)，当且仅当 \(a_i > a_j\) 时，\(i + 1 \sim j - 1\) 差点有贡献的点会有贡献。
所以我们可以对于任意一对下标算出交换后的 \(f(p)\)。
考虑有用的交换对不会很多。有 \(\forall i, (i, a_i)\)。还有对于每个差点有贡献的点，左边比它大的元素和右边比它小的元素交换。一共至多 \(2n\) 对。枚举即可。
54. UVA10735 混合图的欧拉回路 Euler Circuit
有向图有欧拉路径的充要条件是弱连通且每个点入度和出度相等。
先给无向边随意定向，得出每个点的出度减入度的值 \(d_i\)。若 \(d_i > 0\) 说明它需要给一些相邻的点这么多的值，\(d_i < 0\) 说明它需要接受这么多值。
显然可以二分图建图后网络流求出一组给值的方案。这样每个点入度和出度就平衡了。再跑欧拉回路即可。
55. P6943 [ICPC2018 WF] Conquer The World
这题，好怪。
考虑用每个正点权去匹配每个负点权。那么一对匹配的代价是 \(dep_u + dep_v - 2dep_{\text{lca}(u, v)}\)。
考虑自下至上枚举 \(w = \text{lca}(u, v)\)。就是让尽量多的点权在这个点被匹配。匹配完一对我们把它们的点权设成 \(2dep_w - y, 2dep_w - z\)，就是说之后再选到就表示反悔。
因为我们要强制让所有负点权都得到匹配，于是把每个负点权的初始代价加上 \(-\infty\) 即可。这样每个点上的匹配只要代价 \(< 0\) 就继续进行。
56. CF1383F Special Edges
发现 \(k\) 很小，考虑先不管那 \(k\) 条边跑出来一个残量网络，然后最大流转最小割，枚举 \(k\) 条边的一个割的子集。
所以我们现在要求出 \(f_S\) 表示钦定 \(S\) 集合中的边全部保留的最小割。把 \(S\) 集合中的边的容量设为 \(25\)，其他特殊边的容量设成 \(0\) 即可。因为若最优解割了 \(S\) 中的边一定不优，这种方案不会对答案有贡献；否则 \(25\) 就够了。
因为容量很小，所以每次 FF 增广一条路径，在集合中去掉一条边的残量网络上跑，复杂度就是 \(O(\text{maxflow}(n, m) + 2^k wm)\)。
57. P5996 [PA2014] Muzeum
考虑最大权闭合子图，第 \(i\) 个手办建点 \(i\)，第 \(i\) 个警察建点 \(i'\)。我们有一些边：\(\forall i, (S, i, v_i), (i', T, v_i)\)，以及对于能看见第 \(i\) 个手办的第 \(j\) 个警察，有 \((i, j', \infty)\)。手办的 \(\sum v_i\) 减去最小割（最大流）即为答案。
考虑转换坐标系，\((x, y) \to (hx + wy, hx - wy)\)。那么第 \(i\) 个警察能看见第 \(j\) 个手办当且仅当 \(x_i \ge x_j \land y_i \le y_j\)。
但是显然最大流复杂度会炸。考虑模拟最大流。下面部分和 CF1895G Two Characters, Two Colors 有点类似。
首先显然把警察和手办都按 \(x\) 排序。那么我们扫警察时可以先处理 \(x\) 这维的偏序。
我们可以先让 \(v_i\) 的流量从 \(S\) 流到 \(i\)。然后用一个二元组 \((y, v)\) 表示一个纵坐标为 \(y\) 的点还有 \(v\) 单位流量。那么我们扫警察时把所有 \(x\) 比它小的二元组加入。
然后我们现在对于一个警察，它还能往汇点流 \(v_i\) 的流量。考虑贪心地从 \(y\) 坐标不小于它且最小的二元组获取流量。因为 \(y\) 越小的二元组可能的连边就越少，我们从 \(y\) 更大的二元组获取流量不会变优。
所以我们用 set 维护这些二元组，就可以直接 lower_bound 找对应的二元组了。
时间复杂度 \(O((n + m) \log m)\)。
58. P4307 [JSOI2009] 球队收益 / 球队预算
考虑先把全部比赛当成输，那么一次比赛可以让二者中的一个的胜利场次 \(+1\)，失败场次 \(-1\)。
那么新的费用就是 \(c_i \times (x + 1)^2 + d_i \times (y - 1)^2\)。这玩意是单调的，所以可以直接拆边（处理平方的常见技巧）。
59. CF863F Almost Permutation
求出每个位置的上界和下界 \([l_i, r_i]\)。然后每个位置作为左部点，每个数作为右部点连边。为处理平方代价考虑拆点，\(i\) 向汇点连容量为 \(1\)，费用分别为 \(1, 3, 5, \ldots\) 的边即可。
60. CF1307G Cow and Exercise
考虑最优策略是把若干条不交的最短路改成权值相等。
我们可以考虑费用流建图，\(u \to v\)，容量为 \(1\)，费用为边权。这样每次 EK 增广 \(1\) 点流量可以看作找到了新的一条最短路。设流了 \(i\) 单位流量的最小费用为 \(a_i\)。那么 \(ans = \min \frac{a_i + x}{i}\)。
61. CF1599F Mars
考虑对于 \(k = 2 \sim 10\) 依次判断区间内的 \(\sum a_i^k\) 是否等于指定值。
等差数列的首项容易计算。那么 \(\sum\limits_{i = 0}^{n - 1} (a + id)^k\) 就拆开二项式定理即可。
62. P3346 [ZJOI2015] 诸神眷顾的幻想乡
考虑一条路径一定能找到一个叶子，使得以它为根后这条路径是直上直下的。
于是我们遍历所有叶子，把所有从上到下的路径放到广义 SAM 上。然后建广义 SAM 即可。
不同子串个数就是 \(\sum \text{len}(i) - \text{len}(\text{link}(i))\)。
63. CF1383E Strange Operation
还没见过这个套路。
发现题目操作是删除任意一个 \(0\)，或者删除任意一个两边至少有一个 \(1\) 的 \(1\)。
也就是说一个 \(1\) 的连续段不能删没。
考虑如何数本质不同的可以被生成的子序列。我们考虑最后剩下的一个 \(S\) 的子序列 \(T\)，如何判断 \(T\) 能否被生成。
考虑贪心地维护 \(T\) 在 \(S\) 的一个匹配位置。
那么当 \(T\) 后面接了一个 \(1\)，我们跳到 \(S\) 的下一个 \(1\) 位置即可。
当 \(T\) 后面接了一个 \(0\)，如果 \(S\) 的下一个位置不是 \(0\)，我们要跳到最近的一个比这一个 \(0\) 连续段长的连续段。这个可以单调栈求。
所以我们设 \(f_i\) 为以 \(i\) 结尾的子序列数量。转移枚举下一个接的字符，预处理出 \(a_{i, 0/1}\) 表示 \(i\) 下一个接 \(0\) 或 \(1\) 跳到的位置。然后直接 \(f_{a_{i, 0}} \gets f_i, f_{a_{i, 1}} \gets f_i\) 即可。
前后缀的 \(0\) 特殊处理。我们钦定子序列一定以 \(1\) 结尾即可。
64. CF855F Nagini
正负数分别开两棵吉司机线段树即可。只有一个集合正数和负数都加入了，再把它加入第二棵正 / 负线段树。
65. CF536E Tavas on the Path
弱智 *3100。显然所有的 \(1\) 段可以树剖维护，把询问和边按边权排个序，从大到小加入，相当于把一个 \(0\) 变成 \(1\)，再套个树剖就做完了。树剖注意合并顺序。
66. CF1312G Autocompletion
考虑直接在题目给的 Trie 上 dp，设 \(f_u\) 为打出 \(u\) 结点的串的最小代价。
- 首先我们有 \(f_u \gets f_{fa_u} + 1\)。
- 我们有 \(f_u \gets \min\limits_v f_v + t + 1\)，要求 \(u\) 是某个串的终止结点，\(v\) 是 \(u\) 的祖先，\(t\) 是字典序大于等于 \(v\)，小于 \(u\) 的串的个数。
发现我们可以把 \(f_u\) 扔进一个可删堆里，每个点按字典序遍历对应的子结点，每次经过一棵子树就给这个堆打一个整体加这棵子树大小的 tag。这个可以直接用一个变量维护 tag。
时间复杂度 \(O(n \log n)\)。
67. CF382E Ksenia and Combinatorics
考虑 dp，设 \(f_{i, j, 0/1}\) 表示大小为 \(i\) 的树有 \(j\) 对匹配，根是否还能匹配。
转移枚举左右子树大小和匹配数即可。
注意因为左右子树不能交换所以枚举的左右子树不能重，并且相等时要 \(\times \frac{1}{2}\) 来处理交换的情况。
68. [ABC332G] Not Too Many Balls
没做出来。
考虑最大流转最小割。我们枚举和 \(S\) 连通的左部点点集 \(P \subseteq X\) 和和 \(T\) 连通的右部点点集 \(Q \subseteq Y\)。那么此时的最小割为：
观察到 \(\sum\limits_{i \in P} i\) 很小。考虑枚举 \(k = \sum\limits_{i \in P} i\)，那么后面那坨东西的答案就是 \(\sum\limits_{j \in Y} \min(jk, b_j)\)。
前面 \(\sum\limits_{i \in X \setminus P} a_i\) 可以背包求出来。从小到大枚举 \(k\)，显然对于一个 \(j\)，\(jk\) 和 \(b_j\) 的大小关系只会变化一次。排序后双指针处理一下即可。
时间复杂度 \(O(n^3 + m)\)。
69. BZOJ3864 Hero meet devil
dp 套 dp，状压 \(\text{LCS}\) 差分数组即可。
70. P5359 [SDOI2019] 染色
dp 好题。
首先有一个显然的状态，设 \(f_{i, x, y}\) 为第 \(i\) 列上下两格的颜色分别为 \(x, y\) 的方案数。但是这样做时间复杂度至少为 \(O(nm^2)\)，无法接受。
注意到全 \(0\) 列的转移是重复的。我们可以试着只在两个相邻非全 \(0\) 列转移。这样我们需要预处理全 \(0\) 列的转移系数。
我们考虑预处理转移系数时把一段全 \(0\) 列的旁边两列的数的不等关系记入状态中。一共只会有 \(7\) 种本质不同的状态，而其中 \(2\) 对状态是等价的，所以实际上只有 \(5\) 种状态：
0: 1: 2: 3: 4:
a..a a..b a..a a..b a..b
b..b b..a b..c b..c c..d
---- ----
a..c a..c
b..b b..a
其中相同字母代表的数相同，不同字母代表的数不同。
所以我们设 \(g_{i, j}\) 表示一段全 \(0\) 列的长度为 \(i\)，相邻两列的状态为 \(j\)，全 \(0\) 列填法的方案数。
注意到这个东西是可以递推的。以 \(g_{i, 4}\) 的转移为例。
若上一列的状态为 \(0\)：
a..ac
b..bd
其中 ab 之前已经确定，所以转移系数为 \(1\)；
若上一列的状态为 \(1\)：
a..bc
b..ad
转移系数为 \(1\)；
若上一列的状态为 \(2\)：
a..ac
b..cd
a..cc
b..bd
其中上一列的 c 还没确定（注意两列的 c 不同），两种方案 c 都有 \(m - 3\) 种方案，所以转移系数为 \(2m - 6\)。
若上一列的状态为 \(3\)：
a..bc
b..cd
a..cc
b..ad
转移系数为 \(2m - 6\)；
若上一列的状态为 \(4\)：
a..cc
b..dd
考虑分类讨论。若上一列的 c 等于这一列的 d，那么上一列的 d 有 \(m - 3\) 种取值；否则上一列的 c，d 各有 \(m - 4\) 种取值，因此转移系数为 \((m - 4)^2\)。
因此：
再来考虑相邻非全 \(0\) 列的转移。设 \(f_{i, j}\) 表示考虑了前 \(i\) 列，第 \(i\) 列空着的那列填了 \(j\) 的方案数（若第 \(i\) 列上下都填了数则 \(j\) 只在 \(a_{i, 1}\) 处有值）。设上一个非全 \(0\) 的列为 \(k\)，\(t = i - k - 1\) 表示中间全 \(0\) 列的数量。
这里要讨论的情况非常多。以上一个和当前非全 \(0\) 列都只有第一行填了数为例。
若两列第一行填的数相同：
a..a
?..b
此时 \(f_{i, j}\) 的 \(j\) 代表 b 处的值。若 ? 处的值为 \(j\)，那么此时的状态为 \(0\)；若 ? 处的值不为 \(j\)，那么此时的状态为 \(2\)。我们有：
若设 \(s = \sum\limits_{j = 1}^m f_{k, j}\)，我们有：
若两列第一行填的数不同，讨论第 \(i\) 列第二行填的数与第 \(k\) 列第一行填的数是否相同：
a..b
?..a
a..b
?..c
设 a 处的值为 \(x\)，b 处的值为 \(y\)。我们有：
剩下情况的讨论见代码。
还要讨论前缀全 \(0\) 列和后缀全 \(0\) 列。前缀全 \(0\) 列在初始化 \(f\) 数组时讨论。后缀全 \(0\) 列给答案乘上一个系数即可。
需要特判全部列都是全 \(0\) 列的情况。
考虑优化。发现我们对于 \(f\) 数组只会进行全局乘，全局加，单点查，全局查，单点修改的操作。例如 \(f_{i, j} = f_{k, j} g_{t, 0} + (s - f_{k, j}) g_{t, 2}\)，可以看成是先全局乘 \(g_{t, 0} - g_{t, 2}\) 再全局加 \(s \times g_{t, 2}\)。对于不符合条件的状态赋值 \(0\) 可以看成是区间乘 \(0\) 操作。
这样我们可以用线段树维护 \(f\) 数组。转移进行对应的全局乘和全局加操作即可。
时间复杂度 \(O(n \log m)\)。但是考虑到全部操作都是全局和单点的操作，所以应该可以仿照这题的方法优化到 \(O(n)\)。
71. LOJ6499 「雅礼集训 2018 Day2」颜色
考虑分块套 bitset，为了查整块的贡献可以 ST 表。块长设为 \(\left\lceil\frac{n}{64}\right\rceil\)。平衡后时间复杂度 \(O(\frac{n^2}{\omega})\)。
72. [ABC335G] Discrete Logarithm Problems
考虑若我们对于每个 \(a_i\) 求出来了使得 \(g^{b_i} \equiv a_i \pmod P\) 的 \(b_i\)（其中 \(g\) 为 \(P\) 的原根），那么 \(a_i^k \equiv a_j \pmod P\) 等价于 \(kb_i \equiv b_j \pmod{P - 1}\)，有解的充要条件是 \(\gcd(b_i, P - 1) \mid b_j\)。
显然我们不可能对于每个 \(a_i\) 都求出来 \(b_i\)。注意到我们只关心 \(c_i = \gcd(b_i, P - 1)\)，而 \(c_i\) 为满足 \(a_i^{c_i} \equiv 1 \pmod P\) 的最小正整数。若求出 \(c_i\) 则等价于统计 \(c_i \mid c_j\) 的对数。于是问题变成求出 \(c_i\)。
因为我们一定有 \(a_i^{P - 1} \equiv 1 \pmod P\)，所以 \(c_i\) 一定为 \(P - 1\) 的因数。所以我们初始令 \(c_i = P - 1\)，然后对 \(P - 1\) 分解质因数，依次让 \(c_i\) 试除 \(P - 1\) 的每个质因子，判断除完后是否还有 \(a_i^{c_i} \equiv 1 \pmod P\) 即可。这部分复杂度大概是 \(O(n \log^2 P)\) 的。
问题还剩下统计 \(c_i \mid c_j\) 的对数。因为 \(c_i\) 为 \(P - 1\) 的因数，所以我们可以做一遍 Dirichlet 后缀和求出 \(f_x\) 表示满足 \(x \mid c_i\) 的 \(i\) 的个数。最后遍历 \(c_i\) 统计即可。
总时间复杂度大概是 \(O(n \log^2 P + m \log m \log P)\)，其中 \(m\) 为 \(P - 1\) 因数个数。
73. P5287 [HNOI2019] JOJO
考虑离线建操作数 dfs。把一个 \((x, c)\) 缩成一个字符。
kmp 自动机找 fail。前面的一个字符对当前的 fail 的贡献是一段区间赋值和等差数列。主席树维护即可。
74. CF1920F2 Smooth Sailing (Hard Version)
首先需要知道的一个 trick：判断一个点是否在一个闭合回路内部，从这个点向任意方向引一条射线，若不考虑相切，那么和回路的交点为奇数时这个点在回路内部，否则在外部。
那么这题要判断一个回路是否包含全部的 island，可以找到任意一个 island 向右引一条射线。
给每个点增加一个状态 \((x, y, 0/1)\) 表示当前走到 \((x, y)\)，穿过了偶数或奇数次射线。那么一次询问的本质是找到一条 \((x, y, 0) \to (x, y, 1)\) 的一条经过点权最小值最大的路径（可以多源 bfs 求出任意一点 \((i, j)\) 到最近的 v 的距离 \(d_{i, j}\)，\((x, y, 0/1)\) 的点权就是 \(d_{x, y}\)）。
上面那个问题显然给每条 \((u, v)\) 赋权 \(\min(val_u, val_v)\)，就可以建 Kruskal 重构树查 LCA 解决。
建图就对于一个 \((x, y)\)，如果它在射线上就视为 \((x, y) \to (x + 1, y)\) 和射线新增了一个交点。
时间复杂度 \(O((nm + q) \log nm)\)。
75. 2023.1.14 模拟赛 lis
考虑最小割。设 LIS 为 \(m\)。建图：\(\forall f_i = 1, (S, i, 1), \forall i, (i, i', 1), \forall f_i = m, (i, T, 1), \forall f_i + 1 = f_j, i < j, a_i < a_j, (i', j, 1)\)。本质就是要让 \(f_i = 1\) 的点不能到达 \(f_i = m\) 的点。
虽然可以优化建图但是复杂度会炸。考虑直接模拟最大流。发现对于每一条流我们能将其调整为最靠左上的流（如果把 \((i, a_i)\) 视为二维平面上的一个点）。所以我们暴力每次找最靠前的流。递归判断能不能增广。考虑过一个点就把它删掉，无论它能不能增广。这样复杂度就是 \(O(n \log n)\)。
76. CF1916G Optimizations From Chelsu
玄学题。
路径问题考虑点分治。我们考虑一对来自不同子树的 \((g_1, len_1), (g_2, len_2)\) 的贡献。
设 \(len_1 \ge len_2\)，那么 \(g_1 = \gcd(g_1, g_2)\)，否则不优。
那么我们设 \(g_2 = k \times g_1\)。那么要使得这个东西有贡献，我们需要 \(k \le len_1\)。
然后我们枚举 \(k\)，从前往后和从后往前各枚举一遍儿子，暴力枚举 \(k\) 更新答案。然后如果 \(g_1 \times (len_1 + d) \le ans\) 那么这个 \(g_1\) 一定不会有贡献了，直接退出。
77. P5807 【模板】BEST 定理 | Which Dreamed It
BEST 定理：有向欧拉图的本质不同欧拉回路数为：
其中 \(T\) 为以起点为根的外向树个数，可以矩阵树定理求。
78. [ABC336G] 16 Integers
首先考虑只要求构造任意一个符合条件的 \(a\) 怎么做。考虑建图，\((i, j, k, l)\) 向 \(\forall x \in \{0, 1\}, (j, k, l, x)\) 连有向边。那么就是要求固定每个点经过次数的一条哈密顿路径。
但是哈密顿路径仍然不好处理。考虑拆点，把原来的 \((i, j, k, l)\) 看成 \((i, j, k)\) 向 \((j, k, l)\) 连有向边。那么要求固定每条边经过次数的欧拉路径。到这一步直接跑欧拉路径就行了。
考虑如何计数。考虑 BEST 定理，有向欧拉图的本质不同欧拉回路数量（循环同构视为本质相同，每条边互相区分）为：
其中 \(T\) 为图的外向生成树个数（注意到有向欧拉图以每个点为根的外向生成树个数相等），\(out_i\) 为 \(i\) 点的出度。\(T\) 可以用矩阵树定理求得。注意去除孤立点。
但是这题统计的是欧拉路径。考虑原图若存在一对入度小于出度和入度大于出度的点，那么以它们为起点和终点，否则枚举每个点作为起点和终点即可。从终点向起点连一条有向边就转化成了欧拉回路。
注意判一些无解的情况。
时间复杂度 \(O(n^4 + \sum out_i)\)，其中 \(n = 8\)。
79. [AGC051D] C4
下文的点 \(1, 2, 3, 4\) 对应原题面中的 \(S, T, U, V\)。
直接对无向图欧拉回路计数不太好做。考虑给边定向。枚举有 \(i\) 条边是从 \(1\) 到 \(2\) 的。那么 \(2 \to 1\) 有 \(a - i\) 条边。由于这个图必须满足每个点的入度等于出度，设 \(j\) 条 \(2 \to 3\) 的边，\(b - j\) 条 \(3 \to 2\) 的边，那么我们有 \(a - i + j = i + b - j\)。解得 \(j = i + \frac{b - a}{2}\)。同理有 \(k = j + \frac{c - b}{2}\) 条 \(3 \to 4\) 的边，\(l = k + \frac{d - c}{2}\) 条 \(4 \to 1\) 的边。
这样我们就将题目的无向图转化成了有向图。在这个图上做欧拉回路计数。可以考虑 BEST 定理，有向欧拉图的本质不同欧拉回路数量（循环同构视为本质相同，每条边互相区分）为：
其中 \(T\) 为图的外向生成树个数（注意到有向欧拉图以每个点为根的外向生成树个数相等），\(out_i\) 为 \(i\) 点的出度。
这题要求欧拉回路从 \(1\) 出发和结束。每一条欧拉回路 \(1\) 都出现了 \(out_1\) 次，把循环同构的加上，所以答案乘上 \(out_1\)。注意这题每条同方向的边互不区分，所以答案乘上 \(\frac{1}{i! (a - i)! j! (b - j)! k! (c - k)! l! (d - l)!}\) 即可。
时间复杂度 \(O(a + b + c + d)\)。
注意判一些无解的情况，比如 \(i, j, k, l\) 不在范围内。
80. HDU5121 Just A Mistake
考虑拆贡献，统计一个点在集合中的方案数。
考虑一个 dp。\(f_{i, j}\) 表示 \(i\) 在 \(i\) 子树内是第 \(j\) 个，并且 \(i\) 在 \(S\) 中的方案数。
转移考虑容斥，接上一棵子树只会对当前的 \(u\) 有影响。那么 \(v\) 的贡献就是 \(sz_v!\) 减去 \(v\) 在 \(u\) 前面的方案。树形背包合并即可，转移系数为合并两个序列的方案数。
81. HDU6094 Rikka with K-Match
考虑费用流模型，可以发现这个东西是凸的。考虑 wqs 二分。变成最小权任意匹配。轮廓线 dp 即可。设 \(f_{i, j, S}\) 表示考虑到 \((i, j)\)，前面 \(m\) 个是否在匹配内的状态是 \(S\)。
要特别注意一下 wqs 二分的斜率上界，是 \(10^9 nm\) 级别的。
时间复杂度 \(O(nm2^m \log V)\)。
82. Gym102268J Jealous Split
发现一个东西，\(\sum s^2\) 最小的分割一定符合条件。
wqs 二分，压力给到构造方案。可以求出每个位置分的最少和最多的段数。然后不断往前跳，如果下一个位置能被转移过来，并且剩下还要分的段数在这个点分的最少和最多的段数之间，就可以跳。
83. CF1266F Almost Same Distance
好厉害。
特判 \(k = 1\)。首先经过观察，我们可以按照 \(k\) 的奇偶性讨论：
- \(k\) 为偶数，有一个中心点挂了若干条长度为 \(\frac{k}{2}\) 的链。
- \(k\) 为偶数，有两个中心点，两边挂了若干条长度为 \(\frac{k}{2}\) 的链；
- \(k\) 为奇数，有一个中心点挂了若干条长度为 \(\frac{k + 1}{2}\) 的链和至多一条长度为 \(\frac{k - 1}{2}\) 的链。
根据上面我们有 \(ans_k \ge ans_{k + 2}\)。最后取个后缀 \(\min\) 即可。接下来考虑如何处理这 \(3\) 种贡献。
我们可以把每个点的每棵子树挂的最长链预处理出来。然后按照这个长度扫描线。设当前点 \(u\) 出现次数为 \(b_u\)。
对于第一种贡献，可以直接让 \(ans_{2i} \gets b_u\)。
对于第二种贡献，我们要讨论 \(u\) 的所有邻居。维护 \(c_u\) 表示 \(u\) 的所有儿子的 \(b_u\) 的最大值。然后让 \(ans_{2i} \gets \max(b_u + c_u - 2, b_u + b_{fa_u} - 2)\) 即可。\(-2\) 是因为两棵子树互相重复贡献了。
对于第三种贡献，若 \(u\) 是在长度 \(i\) 中第一次出现，有 \(ans_{2i + 1} \gets b_u\)，否则 \(ans_{2i - 1} \gets b_u\)。
时间复杂度 \(O(n)\)。
84. CF1500C Matrix Sorting
做了好久。怎么会是呢。
题目的操作可以看成，求出一些关键字，使得 \(B\) 矩阵的行是由 \(A\) 按照这些第 \(1\) 关键字、第 \(2\) 关键字一直到第 \(k\) 关键字，最后还有一个原来所在行下标的关键字，从小到大排序。
肯定是从排好序的 \(B\) 矩阵入手。首先任意找到一个在 \(B\) 矩阵中已经排好序的列。然后把这一列极长的相等段拎出来，把 \([1, n]\) 分成了若干个区间 \([l_1, r_1], [l_2, r_2], \ldots, [l_k, r_k]\)。发现这是一个递归的过程，我们还要找到一个之前没选过的列，在这些区间分别是升序的。然后可以把这些区间分成一些更小的区间。可以把区间存下来，一轮一轮地判断。
终止条件就是，\([l_1, r_1] \sim [l_k, r_k]\) 都是 \(A\) 矩阵的子序列（因为最后一个排序的关键字是行的下标）。这个可以对每行哈希，然后建子序列自动机判断即可。
但是兴冲冲的写了一发，T 了。发现枚举每一列再判断在这些区间是否分别升序会使得复杂度退化至 \(O(n^3)\)。想起来有个东西叫 bitset。可以把第 \(i\) 行 \(B_{i, j} < B_{i + 1, j}\) 的所有列下标 \(j\) 开个 bitset 存起来，那么得到所有升序的行，只需把 \([l_1, r_1 - 1] \sim [l_k, r_k - 1]\) 的 bitset 与起来就行了。时间复杂度变为 \(O(\frac{n^3}{\omega})\)。
子序列自动机部分若开 vector 存位置然后每次二分就是 \(O(n^2 \log n)\)。但是也能过。跑得还不慢。
85. CF176E Archaeology
\(k\) 个点的虚树大小是按 dfn 排序后 \(\frac{\text{dis}(a_1, a_2) + \text{dis}(a_2, a_3) + \ldots + \text{dis}(a_{k - 1}, a_k) + \text{dis}(a_k, a_1)}{2}\)。set 维护按 dfn 排序后的点，每次处理一下和前驱后继的贡献即可。
86. CF1061E Politics
考虑每个点在两棵树上分别向上找到第一个有限制的祖先。那么 \(\{1, \ldots, n\}\) 可以被划分成若干个集合。
考虑二分图。两棵树的每个集合建个点，和源点或汇点连容量为该集合选的个数，费用为 \(0\)。然后对于树上的每个点，给两边所属集合连一条容量为 \(1\)，费用为 \(a_i\) 的边。跑最大费用最大流即可。
87. P7241 [COCI2019-2020#4] Holding
比较谔谔的题。
注意到 \(L \sim R\) 和其他不在 \([L, R]\) 的交换的最优策略下标一定是不降的。直接根据这个 \(O(n^2k)\) dp 即可。
88. [AGC046F] Forbidden Tournament
太厉害了！！！！！！
首先竞赛图有个性质，若存在环则一定存在三元环。
先把 DAG 的情况（一条链）特判了。然后缩点。发现非链底的部分不能存在大小 \(> 1\) 的 SCC。所以枚举非链底的部分有多少点，转化为 SCC 的情况。
发现对于任意点（设为 \(1\) 号点），它的前驱连成一条链，后继也是一条链。
如果前驱有环那么和 \(1\) 可以形成子图。如果后继最后有一个 SCC，考虑拿出前驱的链顶 \(y\)。显然这个 SCC 的点不能全部连向 \(y\)。所以这个 SCC 能分成两个非空集合 \(S_1, S_2\)，满足一个连向 \(y\)，一个被 \(y\) 连。发现 \(S_1\) 不能存在到 \(S_2\) 的边。所以这不是一个 SCC。
设前驱的链为 \(A_{1 \sim a}\)，后继的链为 \(B_{1 \sim b}\)。
首先因为这是一个 SCC 所以一定有 \(B_b \to A_1\) 的边。
然后我们发现对于前驱的点，它一定是有一段连向后继的前缀，剩下的后缀是连向这个点。
设前驱第 \(i\) 个点连向后继的是 \([1, p_i]\)。又发现 \(p\) 单调不降。
然后就可以转化为对于 \(p\) 计数。入度判一下即可。
时间复杂度 \(O(n^4)\)。
89. CF1672F2 Checker for Array Shuffling
做不出题怎么办。
考虑拿出出现次数最多的元素（因为最后的最少交换次数就是最大的出现次数）。那么所有环都必须包含这个元素。所以直接把这个点删掉再判有没有环即可。
90. CF982E Billiard
考虑把平面无限延伸，可以看作是一条斜率为 \(1\) 的直线第一次经过一个横坐标是 \(n\) 倍数，纵坐标是 \(m\) 倍数的点。扩欧解一下即可。
91. P8426 [JOI Open 2022] 放学路（School Road）
考虑整个图是一个点双怎么做。
显然如果有重边并且两条边边权一样就寄了。否则我们可以把它们当成一条边。
考虑一个二度点 \(u\) 和与它相连的边 \((v, u), (u, w)\)。我们可以把它缩成边 \((v, w)\)。如果新边已经存在并且边权不等于这两条边边权就寄了。缩点可能会产生一些新的二度点，用队列维护。
剩下的点除了 \(1, n\) 是度数 \(\ge 3\) 的点。可以证明如果最后有度数 \(\ge 3\) 的点就一定不行。因为可以得出一条边的边权为 \(0\)，与题设矛盾。
考虑整个图不是点双。考虑添加边 \((1, n, \text{dis}(1, n))\)。只保留和 \(1, n\) 在同一个点双的点即可。因为不在就不能从 \(1\) 到这个点再到 \(n\)。
然后就转化成了整个图是一个点双，用上面的做法即可。
时间复杂度 \(O((n + m) \log n)\)。
92. CF652F Ants on a Circle & [AGC013C] Ants on a Circle
是不是经典问题啊。
不考虑编号，那么碰到就调头可以看作是直接继续走。
因为碰到就调头，所以蚂蚁的相对位置不会变。
但是我们如果直接用终点位置 sort，得到的序列只是最终答案的一个循环位移。
考虑维护编号的偏移量。若视为一条链，若一只蚂蚁顺时针跨过了 \(k\) 次 \(m\) 的倍数的位置，因为是在环上，那么最后 \(1\) 号蚂蚁的位置会增加 \(k\)，否则增加 \(-k\)。根据这个算就行。
93. CF1778F Maximizing Root
这是什么傻逼题。
直接设 \(f_{i, j}\) 为 \(i\) 子树内使得 \(\gcd = j\) 的最小步数。转移因为有用状态很少所以复杂度是对的。
94. CF814E An unavoidable detour for home
考虑给图分层，一层的点一一对应上一层的一些点。设 \(f_{i, j}\) 为考虑了前 \(i\) 个点，最后一层有 \(j\) 个点，除了最后一层点的其他点度数限制已经满足的方案数。
转移系数是 \(g_{i, j, k}\) 表示这一层有 \(i\) 个点，上一层有 \(j\) 个 \(2\) 度点，\(k\) 个 \(3\) 度点（实际上因为上一层已经和上上层连边所以是 \(1, 2\) 度点）。这个的递推是容易的。
时间复杂度就是 \(O(n^3)\)。
95. CF917D Stranger Trees
考虑钦定一些边是原树的边，其余任意，那么最后的答案可以二项式反演得出。
剩下的是一个二维树形背包，\(f_{u, i, j}\) 表示 \(u\) 子树内包含 \(u\) 的连通块大小是 \(i\)，保留了 \(j\) 条边。要记第二维是因为大小为 \(\{s_k\}\) 的连通块形成一棵无根树的方案数是 \(n^{k - 2} \prod s_i\)。
时间复杂度 \(O(n^4)\)。有 \(O(n^2)\) 做法，就是考虑 \(\prod s_i\) 的组合意义是在每个连通块选一个点的方案数，然后可以把记连通块大小的那维去掉。
96. CF986F Oppa Funcan Style Remastered
有意思的。
对 \(k\) 分解质因数，题目实际上是想让我们解一个 \(\sum\limits_{i = 1}^m a_i x_i = n\) 的方程。
考虑 \(m = 1\) 特判，\(m = 2\) exgcd。\(m = 3\) 时发现 \(\min\limits_{i = 1}^m a_i \le k^{\frac{1}{3}} \le 10^5\)，所以可以跑同余最短路。设 \(f_i\) 为能组成的 \(\bmod a_1 = i\) 的最小数。那么就直接判 \(f_{n \bmod a_i} \le n\) 即可。
同余最短路还在写最短路？感觉不如转圈！
97. CF1148G Gold Experience
考虑取原图的补图。相当于给 \(\gcd(a_i, a_j) = 1\) 的点连边。
那么我们可以选出大小为 \(k\) 的独立集，或者选出 \(k\) 个点，满足每一个点在一个大小 \(\ge 2\) 的连通块内。
考虑先随便找一个独立集，若大小为 \(k\) 就输出。
这一步我们需要维护一个集合，支持插入一个数，询问和它互质的数的个数。可以预处理因数然后莫反解决。
否则，其他不在独立集的点一定是挂在了某个独立集的点上。可以分治（类似整体二分）找到每个独立集的点挂了多少其他点。
因为 \(2k \le m\)，所以一定有一个独立集的点下面挂了至少 \(2\) 个点。于是一定有解。
时间复杂度 \(O(n \log n 2^{\omega(V)})\)。
98. CF1240F Football
挺妙的。
接下来我们将构造一个每条边都染色的方案，所以原来的 \(w_i\) 没用。
极差 \(\le 2\) 这个条件比较谔谔。考虑拆点，把原图变成二分图，那么 \(u, u + n\) 的极差只要都 \(\le 1\)，原图就满足条件。
但是现在还不是很好做。考虑继续拆点。一个点 \(u\) 拆成 \(\left\lceil\frac{deg_u}{k}\right\rceil\) 个点，要求每个点的出边颜色互不相同。
现在就好做了。考虑对于每条边，先找到一个两端没使用过的颜色。如果存在那么直接染色。否则设 \(u\) 没使用过 \(c_1\)，\(v\) 没使用过 \(c_2\)，先强制把这条边染成 \(c_1\)，然后递归找 \(v\) 的颜色为 \(c_1\) 的出边修改成 \(c_2\) 即可。
若成环，因为都是偶环，所以若到 \(u\) 相当于把 \(u\) 的使用过的 \(c_1\) 颜色的出边修改成 \(c_2\)，不符合原有条件。
时间复杂度 \(O(nm^2)\)，因为每次最坏情况会遍历整张图。但是实际跑得挺快的。
99. CF1466H Finding satisfactory solutions
考虑给定 \(b\) 如何构造 \(a\)。
拎出基环树的环部分，把这些点连同它们的边删掉（这个环一定在答案中）。递归做即可。
考虑我们在 \(a\) 的环上连一些在 \(\{b_{i, n}\}\) 中排得比 \(a_i\) 前的 \(i \to j\)。可以将问题转化为，若干个环，缩点后连一些边使得它成为 DAG。
一个 DAG 对应的 \(b\) 的个数就是 \(\prod\limits_{i = 1}^n d_i! (n - d_i - 1)!\)，因为入边和出边在 \(b_i\) 中可以独立地随意排列。
然后考虑经典状压 dp，设 \(f(S)\) 为点集 \(S\) 形成了一个 DAG（缩点之后），对应的 \(b\) 的个数。转移枚举入度为 \(0\) 的集合 \(T\)，乘上一个容斥系数 \((-1)^{|T| + 1}\)，可得：
其中 \(sz_S\) 为环集 \(S\) 的点数。\(g(n, m)\) 为 \(n\) 个点可能连向 \(m\) 个点，那 \(n\) 个点的 \(\prod\limits_{i = 1}^n d_i! (n - d_i - 1)!\) 之和。容易发现这 \(n\) 个点互相独立，于是考虑设 \(h(m)\) 为一个点可能连向 \(m\) 个点的系数。有：
设环数为 \(c\)，那么此时的复杂度为 \(O(3^c)\)，不能通过。注意到因为转移系数只和 \(S, T\) 的大小和点数有关，于是考虑把 \(\{p_c\}\) 压缩进状态，其中 \(p_c\) 为长度为 \(c\) 的环的出现次数。这样 \(n = 40\) 时状态数最大为 \(1440\)，总时间复杂度 \(O(1440^2 c)\)，可以通过。
100. CF750H New Year and Snowy Grid
考虑其对偶问题：左上角和右下角的 . 连通当且仅当在外面加入一圈 # 后左下角与右上角的 # 连通。
类似地，只存在一条路径当且仅当有割点，即添加一个 # 后左下角与右上角连通。
我们称两个连通块几乎连通当且仅当添加一个 # 后它们连通。
添加一些障碍，先把通过障碍使得左下角和右上角几乎连通的情况判掉。只用判和障碍曼哈顿距离 \(= 2\) 的 \(16\) 个点。
还有一种情况就是添加障碍后原来一个几乎连通的连通块对分别和左下角和右上角连通了。因为几乎连通的连通块对数为 \(O(nm)\)，所以可以存起来，合并障碍时和障碍连通的连通块也只有 \(O(k)\) 个，因此可以暴力枚举并判断是否在一开始的几乎连通块对内。
101. CF798E Mike and code of a permutation
考虑若没有标记，那么直接线段树优化建图后拓扑排序即可。
有标记，可以建主席树，每次把主席树上连向 \(a_i\) 的边删掉即可。
102. CF1922F Replace on Segment
直接随便区间 dp 一下，设 \(f_{i, j, k}\) 为使得 \([i, j]\) 均 \(= k\) 的最小操作次数，\(g_{i, j, k}\) 为使得 \([i, j]\) 均 \(\ne k\) 的最小操作次数。转移随便转移一下。时间复杂度 \(O(n^3m)\) 可以通过。不知道为什么是 2500。
103. 2024.1.19 模拟赛 寸又木（eert）
考虑 \(S_1\) 的边若合法一定形成一个外向树森林，并且一个非根结点一定不会有其他的入边，所以可以把整棵树缩起来。
然后我们考虑，若存在合法解，我们随意按照一个顺序 dfs，第一个访问完所有点的点一定是外向树的根。然后得到这个根再 dfs 一遍构造方案即可。
遍历补图是经典技巧，用 set 存被 ban 的出边，并查集维护每个点下一个没被访问的点，复杂度就是对的。
104. P5491 【模板】二次剩余
考虑若有非 \(0\) 解，那么两个解在模意义下互为相反数。
判定 \(n\) 在模 \(p\) 意义下是否有二次剩余，只要看 \(n^{\frac{p - 1}{2}}\) 为 \(1\) 还是 \(-1\) 即可。
Cipolla 算法流程是，任意随一个 \(a\) 使得 \(a^2 - n\) 不是二次剩余。设 \(i^2 \equiv a^2 - n \pmod p\)，注意此时 \(i\) 是模意义下的虚数。
然后可以推出 \(i^p = i \times (i^{\frac{p - 1}{2}})^2 \equiv -i \pmod p\)。所以 \((a + i)^{p + 1} = (a + i)^p (a + i) = (a^p + i^p)(a + i) = (a - i)(a + i) = n\)。那么 \((a + i)^{\frac{p + 1}{2}}\) 为其中一个解。
可以反证法说明 \((a + i)^{\frac{p + 1}{2}}\) 不会存在虚部。假设 \((A + Bi)^2 \equiv n \pmod p\)，其中 \(B \ne 0\)，展开得 \(A^2 + 2ABi + B^2 i^2 \equiv n \pmod p\)，即 \(A^2 - n + B^2 (a^2 - n) \equiv -2ABi \pmod p\)。那么 \(AB \equiv 0 \pmod p\)，又因为 \(B \ne 0\)，所以 \(A \equiv 0 \pmod p\)，那么 \(B^2 i^2 \equiv n \pmod p\)，即 \(i^2 \equiv nB^{-2} \pmod p\)。所以 \(i^2\) 存在二次剩余，矛盾。
具体实现时需要实现虚数类。
105. P10063 [SNOI2024] 平方数
考虑一个求二次剩余时需要用到的结论：一个非完全平方数在模奇质数下有接近 \(\frac{1}{2}\) 的概率不是二次剩余。
所以我们随 \(50\) 个 \(10^5\) 级别的小质数（不能随大了，因为要快速算 \(x^{\frac{p - 1}{2}}\)），然后考虑把一个前缀的乘积在这 \(50\) 个质数下是否为二次剩余压进一个状态里面。那么若 \([l, r]\) 乘积为完全平方数那么 \([1, l - 1]\) 和 \([1, r]\) 的状态一定相等，否则有极大的概率不会相等（出错概率可以忽略不计）。然后就可以直接统计了。
106. 2024.1.20 模拟赛 T1 旅行者（travel）
感觉我的做法比较有启发性。
考虑 dp，设 \(f_u\) 为序列以 \(u\) 结尾的方案数，那么 \(u\) 能转移到 \(v\) 当且仅当存在一条 \(u \to v\) 的路径满足路径上的点出了 \(v\) 编号都 \(\le u\)。
首先建出大根点重构树，可以参考这题的建法，就是按编号从小到大枚举，遍历比它小的出边，并查集找一下祖先再连边。这样两点 LCA 为它们路径点编号最大值的最小值。
然后就能在树上做了。\(u\) 能转移到 \(v\) 当且仅当 \(u\) 子树内存在一条到 \(v\) 的出边。
考虑被动转移，即考虑 \(f_u\) 能被哪些点转移。发现是一些链的并。想到建虚树，那么 \(f_u\) 为每条边的链的 \(f\) 的和之和。实际上不用显式建出虚树，使用虚树的 dfn 排序后 lca 连边的构建方法即可。
发现瓶颈在 \(O(n \log^2 n)\) 的链的 \(f\) 的和。发现一条链除了最上方的重链外都已经完全遍历过，且这些贡献是一些从上往下的前缀和。那么我们完全可以在计算完链顶的 \(f\) 值后做一遍前缀和，所以只有最后一条链需要在树状数组上查询。所以可以做到单 \(\log\)。
107. P8189 [USACO22FEB] Redistributing Gifts G
有一个脑子被吃掉的人不会状压数环，我不说是谁。
考虑若求出 \(h_S\) 表示 \(S\) 集合内恰好形成一个置换环的方案数，那么可以求 \(g_S\) 表示 \(S\) 集合形成若干个置换环的方案数，于是可以快速回答询问。
求 \(h_S\) 是经典问题。考虑从环上编号最小的点断环为链，设 \(f_{S, i}\) 为链经过了 \(S\) 集合中的点，结尾是 \(i\) 的方案数。就可以直接枚举下一个点转移。
然后时间复杂度是 \(O(2^n n^2 + 3^n + q)\)。很抽象对吧。但是为啥不会呢。
108. [AGC010E] Rearranging
赛时在想一些奇怪的东西，没想到建图。
考虑使用元素两两之间的相对顺序来描述序列。发现若 \(x, y\) 互质那么它们的相对顺序被确定了。
先把输入的序列从小到大排序。然后考虑互质的数之间先连一条无向边。那么先手要把无向边定向使得它是个 DAG，后手会求出这个 DAG 的最大拓扑序。也就是说先手要最小化这个 DAG 的最大拓扑序。
考虑把所有点的边按编号从小到大排序，然后从小到大遍历这个图，从小到大遍历出边，这样会形成一个生成森林，边从祖先定向到儿子即可。
考虑这样贪心为什么是对的。发现若先遍历更大的点 \(v_2\) 肯定不优，因为若先遍历更小的点 \(v_1\)，说不定就在遍历 \(v_1\) 的过程中访问了 \(v_2\)，就能使得不用添加 \(u \to v_2\) 的边。所以是不优的。
时间复杂度为 \(O(n^2 (\log V + \log n))\)，\(\log V\) 为求 \(\gcd\) 复杂度。
109. [ABC337F] Usual Color Ball Problems
哎呀，这下搞笑了，做不出来黄题。
原来这题啥数据结构都不用。
双指针，维护一个 \(s\) 表示当前用的盒子个数。每种颜色维护一个 \(b_i, c_i\) 分别表示该颜色占用的盒子个数和该颜色的出现次数。那么直到 \(s < m\) 都可以更新。更新是 \(O(1)\) 的。总时间复杂度是 \(O(n)\)。
不明白我赛时在想什么，甚至还看错了一次题。
110. CF342E Xenia and Tree
比较谔谔，为什么题解区都在群魔乱舞。不是有个很简单的点分树做法吗。
考虑建出点分树，由点分树的性质可得任意两点在点分树上的 LCA 一定在它们的路径上。然后每次暴力跳父亲，每个分治中心维护一个 \(f_i\) 表示距离 \(i\) 最近的红色点的距离即可。
若使用 dfn 序 st 表求 lca，时间复杂度为 \(O((n + m) \log n)\)。
有操作分块的做法，大概懂了。就是每 \(O(\sqrt{m})\) 次操作分块，遍历到块左端点时先预处理出所有点到红色点的最短距离，然后块内只会加入 \(O(\sqrt{m})\) 个红色点，这部分可以暴力枚举。总时间复杂度 \(O(n \sqrt{m})\)。
111. CF1553G Common Divisor Graph
纯傻逼。考虑答案不超过 \(2\)，因为 \(2 \mid \gcd(a_s (a_s + 1), a_t (a_t + 1))\)。
考虑把 \(0, 1\) 的情况判掉，剩下就是 \(2\)。
考虑对质因子建图，一个 \(a_i\) 看成一些边。那么 \(0\) 是好判断的。
\(1\) 的情况是一个 \(a_i (a_i + 1)\) 的质因子连接了两个连通块，暴力枚举这样的连通块对塞进哈希表或者类似的东西即可判断。
112. CF1098C Construct a tree
考虑一个显然的转化，\(\sum sz_i = \sum dep_i\)。所以要构造一棵 \(\sum dep_i = s\) 的树，使得最大儿子数最小。
考虑二分这个儿子数。也就是二分到 \(x\) 时计算满 \(x\) 叉树的 \(\sum dep_i\)。
然后我们现在有一个满 \(x\) 叉树，其中 \(\sum dep_i \le s\)。我们希望在不影响最大儿子数 \(x\) 的前提下，让 \(\sum dep_i\) 增加至 \(s\)。
考虑从前往后遍历，贪心地判断 \(dep_i\) 是否能增加。算出增加 \(dep_i\) 的最小 \(\sum dep_i\)。如果此时 \(\sum dep_i \le m\) 那么就增加。这样可以覆盖到每一个 \(s\)。
得出每个点的 \(dep_i\) 后考虑构造它的父亲。贪心地选上一层儿子数最小的点当父亲即可。
时间复杂度 \(O(n \log n)\)。
113. [ARC170C] Prefix Mex Sequence
我们实际上并不关心 \(\text{mex}\) 的具体值，只关心它有没有成为 \(\text{mex}\)。
考虑有一个 \(k = \min(m + 1, n)\) 个空位的长条。我们每次可以往长条最左边的空位放一个球（对应 \(a_i\) 成为 \(\text{mex}\)），或者往长条不是最左边的空位或者非空位放一个球（对应 \(a_i < k\) 且 \(a_i\) 不是 \(\text{mex}\)），或者直接把这个球扔掉（对应 \(a_i \ge k\)）。
那么直接设 \(f_{i, j}\) 表示考虑了前 \(i\) 个数，长条占了的空位数为 \(j\) 的方案数。转移考虑 \(a_i\) 的取值个数即可。也就是：
- \(s_i = 1\)：往长条最左边的空位放一个球，有 \(f_{i, j + 1} \gets f_{i - 1, j}\)；
- \(s_i = 0\)：考虑放的球是否占用了空位，有 \(f_{i, j} \gets (j + m - k + 1) f_{i - 1, j}, f_{i, j + 1} \gets (k - j - 1) f_{i - 1, j}\)。
时间复杂度 \(O(n \min(n, m))\)。
114. [ARC170D] Triangle Card Game
赛后调了 40min，哈哈。
首先先把 \(a, b\) 排序。
考虑先枚举 Alice 选的数 \(a_i\)，然后若 \(\forall j, \exists k \ne i, (a_i, b_j, a_k)\) 能组成三角形，Alice 就赢了。
考虑简化条件。\((x, y, z)\) 能形成三角形的充要条件是 \(z \in (|x - y|, x + y)\)。那么条件变为 \(\forall j, \exists k \ne i, a_k \in (|b_j - a_i|, b_j + a_i)\)。
看到有个绝对值，考虑分类讨论。若 \(b_j \le a_i\)，那么 \(a_k \in (a_i - b_j, a_i + b_j)\)。可以发现 \(b_j\) 越小这个范围越窄。所以只用判断 \(b_j\) 最小，即 \(j = 1\) 的情况。这个可以维护一个 multiset，然后 upper_bound 找大于 \(a_i - b_1\) 的最小数判断。
考虑 \(b_j > a_i\)。考虑对每个 \(i\) 求出一个分界点 \(p_i\) 使得 \(b_{p_i}\) 为第一个大于 \(a_i\) 的数。那么条件变为 \(\forall j \ge p_i, \exists k \ne i, a_k \in (b_j - a_i, b_j + a_i)\)。
变形一下可得 \(b_j \in (a_k - a_i, a_k + a_i)\)。
这个条件就比较有意思了。可以把它看成是一个中点为 \(a_k\)，长度为 \(2a_i\) 的线段。考虑把所有 \(a, b\) 排列在数轴上，设 \(b_j\) 夹在 \(a_x, a_{x + 1}\) 之间。那么当 \(a_i \le t = \min(b_j - a_x, a_{x + 1} - b_j)\) 时，\(b_j\) 是不能被覆盖的。所以对于一个 \(i\)，若 \(i \le q_j\) 且 \(j \ge p_i\)，\(i\) 就不满足条件，就不能让 Alice 赢。这是一个二维偏序的形式，考虑第一维扫描线，第二维树状数组维护即可。
然后你写出来这个东西发现被这个 case 卡掉了：
1
2
3 8
4 4
答案是 Bob，而你输出了 Alice。原因是我们没有考虑 Alice 不能选重复的数的情况。考虑若 \(q_j = x\) 就会出现选重复数的情况，若 \(a_{x + 1}\) 不能用长度为 \(2a_x\) 的线段覆盖到 \(b_j\)，即 \(a_x + b_i \le a_{x + 1}\)，就让 \(q_j \gets q_j + 1\)。
总时间复杂度为 \(O(n \log n)\)。
115. CF1098D Eels
考虑最优策略是每次选最小的两个合并，那么答案就是把 \(a\) 排序后总个数减去满足 \(a_i > 2 \sum\limits_{j = 1}^{i - 1} a_j\) 的 \(i\) 的个数。
考虑值域分块，\([2^i, 2^{i + 1})\) 分块。那么块内只有最小的数可能成为满足条件的数。判断一下即可。
116. CF1609F Interesting Sections
看到 \(\max, \min\) 考虑单调栈。枚举右端点，计算有多少个符合条件的左端点。
单调栈维护的是对于每个右端点，以每个点为左端点的后缀 \(\max, \min\) 形成的极长的段。先枚举 \(\text{popcount} = k\)，然后如果一个段的 \(\max\) 的 \(\text{popcount} = k\) 就在线段树上把这段区间 \(+1\)。\(\min\) 同理。那么查询就是查 \([1, n]\) 的 \(2\) 的个数。可以维护区间最大值个数解决。
时间复杂度 \(O(n (\log n + \log V))\)。但是因为 \(\log n\) 是线段树的 \(\log\) 所以要卡常才能通过。
117. QOJ4829 Mark on a Graph
一开始按 time(0) 奇偶性过了，补了一个比较正常的做法。
考虑拎出度数最大的 \(5\) 个点，若它们形成了环就认为是 ok，否则 mark。
118. CF1609G A Stroll Around the Matrix
我独立做出一道 *3000？
考虑对于单次询问，除了 \(O(nm)\) 的 dp，有没有什么方法能快速算出答案。发现若 \(a_{i + 1} - a_i < b_{j + 1} - b_j\) 则 \(i \gets i + 1\)，否则 \(j \gets j + 1\) 是最优的。这个贪心的证明不难，考虑当前新走到某一行或某一列的贡献是差分数组乘上剩下的格子个数，显然选较小的乘上去最优。
那么现在单次询问我们能做到 \(O(n + m)\) 了。观察到 \(n \le 100\)，考虑从这里入手。可以枚举每一行，二分出在这一行能走到的最右的列（也就是最大的 \(j\) 使得 \(b_{j + 1} - b_j < a_{i + 1} - a_i\)）。用一棵树状数组维护 \(b\) 的二阶差分即可树状数组上二分找到这个位置。
\(a\) 对答案的贡献每次枚举 \(i\) 直接计算即可，\(b\) 对答案的贡献不难发现是 \([1, m]\) 的和加上一些单点的形式（单点的贡献是向下走产生的）。查 \(b\) 的单点的值，考虑转化成 \(b\) 的一阶差分的前缀和，也可以用树状数组维护。
总时间复杂度为 \(O((nm + q) \log m + nq)\)。
119. GDOJ8689 蛋糕（cake）
考虑把原序列看成一个折线图，\(1\) 是向上，\(0\) 是向下。那么一次操作相当于交换距离为 \(2\) 的一对 \(10\)，且要求 \(1\) 必须在 \(0\) 前面。
考虑分奇偶性讨论，最后把两部分的方案数互相插入一下乘个 \(\binom{a + b}{a}\) 的系数即可。那么一次操作可以交换相邻的一对 \(10\)。
考虑转化成杨表，相当于给每个格子一个标号，使得每个格子比它左边和上面的数字小。直接套用钩长公式即可：
注意钩长不带阶乘。时间复杂度 \(O(\sum a)\)。
120. CF1611G Robot and Candies
神秘贪心。
按 \(x + y\) 的和从小到大枚举，每次尝试延伸一条路径，若当前的斜线被删空了就跳到下一条斜线。
121. GDOJ8706 赛博航行（saber）
考虑加入一个 \(p_i\) 对答案的贡献。发现若 \(p_i \ge p_{i - 1}\) 贡献为 \(0\)，否则为 \(i - 1\)。
于是树状数组维护差分数组 \(< 0\) 的位置的个数和和即可。
122. CF1201E2 Knightmare (hard)
orz Charlie/bx.
考虑对棋盘染色，那么马移动到的格子和原来的格子异色。
进而发现若两个马初始异色，那么只有白马可以吃黑马，否则只有黑马可以吃白马。
下面只讨论初始异色的情况，同色是对称的。下文令 \(W, B, T_W, T_B\) 分别为白马起点，黑马起点，白马终点，黑马终点。
考虑若白马能比黑马早到终点，即 \(\text{dis}(W, T_W) \le \text{dis}(B, T_B)\)，那么白马直接不管黑马冲到终点就行了，反正黑马也吃不掉它。
否则白马比速度肯定比不过了，就要想办法吃掉黑马。发现如果白马能比黑马早到 \(T_B\) 白马才有可能吃掉黑马。因为题目说另一只马到了终点再吃也算吃掉，所以这里的早到定义为 \(\text{dis}(W, T_B) \le \text{dis}(B, T_B) + 1\)。
那么白马到了 \(T_B\) 后如果还没吃掉黑马，那么此时白马和黑马的距离一定至少为 \(2\)（因为两只马此时位置同色）。黑马肯定不能移动使得它与白马的距离为 \(1\)，否则白马就吃掉它了。所以黑马只能移动使得它与白马的距离为 \(3\)。又因为 \(\text{dis}(T_W, T_B) = 3\)，所以白马直接冲到终点就结束了。
如果不满足 \(\text{dis}(W, T_B) \le \text{dis}(B, T_B) + 1\) 那么白马无法吃掉黑马。这种情况黑马直接冲到终点就能赢，不用管白马。
直接模拟上面的分析过程即可。实现时需要以 \(W, B\) 为起点跑最短路并且记录一下前驱。
123. CF1218A BubbleReactor
虚高 *2800。放模拟赛 T2 人均切了。
考虑拎出环上的点，每个点下面都挂了一棵树。
那么可以预处理出每棵树从一个点开始染黑，这棵树对答案的贡献。因为一棵树染了一个点就只能去染子树了，所以这个贡献是固定的，用换根 dp 求即可。
那么我们现在可以在环上选择一个起点，每次可以把左端点或右端点往外拓展 \(1\)。拓展的贡献就是除了已经拓展的点外其他点挂的树的 \(sz\) 之和，加上要拓展的点的所有子树 \(sz\) 和。
套路区间 dp 即可。设 \(f_{i, j}\) 为已经拓展了环上在 \([i, j]\) 中的点即可。注意因为是个环所以 \(i > j\) 时 \(f_{i, j}\) 表示已经拓展了环上在 \([i, m] \cup [1, j]\) 的点，其中 \(m\) 为环上的点数。
按长度从小到大枚举，就可以滚动数组了。
时间复杂度 \(O(n + m^2)\)。实际跑得挺快。
124. QOJ7206 Triple
大分讨恶心题。
首先施容斥，变成求 \(\sum |AB| > \max(|AC|, |BC|)\)。
遇到这种三个点的路径问题，可以找出一个点 \(X\)，使得 \(A, B, C\) 在 \(X\) 的不同子树内，也就是 \(A \to B, A \to C, B \to C\) 的路径的唯一一个交点 \(X\)。那么：
考虑先点分治，考虑对于一个分治中心 \(R\)，计算 \(A, B, C\) 不是都在同一棵子树的方案。为了方便认为 \(R\) 是单独的一棵子树。
若 \(A, B, C\) 都不在同一棵子树，考虑直接枚举 \(C\)，对子树每个点的深度预处理一个后缀和 \(F_d\) 和在每棵子树选两个深度 \(\ge d\) 的点的方案数 \(G_d\)，为了容斥算出 \(A, B\) 不在同一棵子树的方案数。需要去除 \(C\) 所在子树对 \(F, G\) 的贡献。
若 \(A, C\) 在同一棵子树（\(B, C\) 一样，贡献 \(\times 2\)），考虑枚举 \(X\) 和 \(|CX|\)，那么要求 \(|AX| > |CX|\)，可以用长剖计算这样的对数。还要求 \(|BX| > |CX|\)，即 \(|BR| + |RX| > |CX|\)，即 \(|BR| \ge |CX| - |RX| + 1\)。这部分贡献可以用上部分处理的 \(F\) 数组。
若 \(A, B\) 在同一棵子树，考虑直接枚举 \(X\) 和 \(\min(|AX|, |BX|)\)，也可以用长剖计算 \(X\) 子树内 \(A, B\) 的对数使得 \(\min(|AX|, |BX|) = k\)。还要求 \(|CX| < k\)，即 \(|CR| \le k - |RX| - 1\)。这部分贡献也可以用第一部分处理的 \(F\) 数组。
于是总时间复杂度为 \(O(n \log n)\)。
注意讨论一些 corner case。
125. CF1684F Diverse Segments
考虑扫描线，扫到 \(i\) 时，设包含 \(i\) 的区间的最小左端点为 \(l\)。设 \(x = a_i\)。
若 \([l, i]\) 之间存在 \(\ge 2\) 个 \(x\)，那么就必须要修改。考虑序列此时的形式形如：
考虑若修改的区间左端点 \(\le l\) 右边第一个 \(x\) 的位置，那么修改的区间右端点必须在倒数第二个 \(x\) 位置或其之后。若修改的区间左端点 \(> l\) 右边第一个 \(x\) 的位置但是 \(\le l\) 右边第二个 \(x\) 的位置，那么修改的区间右端点必须在 \(i\) 或其之后。否则修改的区间左端点不可能 \(> l\) 右边第二个 \(x\) 的位置。
若设 \(f_i\) 为修改的区间左端点为 \(i\)，修改的区间右端点的最小值。那么上面就相当于对 \(f\) 的区间取 \(\max\)。最后我们要求出 \(f\) 的每个值，答案即 \(\min\limits_{i = 1}^n f_i - i + 1\)。可以使用线段树维护 \(f\)。
总时间复杂度 \(O(n \log n)\)。
126. SPOJ QTREE5 - Query on a tree V
考虑建点分树，每个分治中心开个可删堆维护子树内全部白点到它的距离。这样查询和修改都可以跳点分树上的父亲暴力做。
因为在同一棵子树内的点对的距离只会变大，所以不用钦定在同一棵子树内。
127. SPOJ QTREE4 - Query on a tree IV
和上题类似，不同之处在于要钦定贡献的点对在不同的子树。考虑每个点再维护一个堆存所有儿子的子树距离最大值。然后这个堆的前两大值的和可能对答案有贡献。仍然可以可删堆维护。
128. CF288E Polo the Penguin and Lucky Numbers
虚高 *2800，放模拟赛 T1 人均切了。
首先我们发现这玩意有可减性，用 \([1, r]\) 的答案减去 \([1, l]\) 即可。所以接下来我们只讨论前缀的情况。
考虑数位 dp。为了计算题目的那玩意我们考虑把每个状态的 dp 值用一个三元组 \((a_1, a_n, \sum\limits_{i = 1}^{n - 1} a_i a_{i + 1})\) 表示。那么这样是可以合并的，\(\sum\limits_{i = 1}^{n - 1} a_i a_{i + 1}\) 变成两边的 \(\sum\limits_{i = 1}^{n - 1} a_i a_{i + 1}\) 之和再加上左边的 \(a_n\) 乘上右边的 \(a_1\) 即可。
但是我们发现我们还要进行让全部 \(a_i\) 加上 \(x = t \times 10^k\) 的操作。考虑 \(\sum\limits_{i = 1}^{n - 1} (x + a_i) (x + a_{i + 1}) = (n - 1)x^2 + x \sum\limits_{i = 1}^{n - 1} (a_i + a_{i + 1}) + \sum\limits_{i = 1}^{n - 1} a_i a_{i + 1}\)。所以我们多维护 \(\sum\limits_{i = 1}^{n - 1} a_i + a_{i + 1}\) 和 \(n\) 即可转移。
时间复杂度 \(O(\log_{10} r)\)。
129. 2024.1.24 模拟赛 T2 欧内的环（lottop）
猜测答案 \(\le 5\)（不然这题就没法做了）。
三元环好处理。考虑判断有没有四元环。仍然沿用三元环的方法，给无向图定向，枚举出边后再在无向图上枚举一个点，若有重复就说明有四元环。
130. P7372 [COCI2018-2019#4] Slagalica
模拟赛赛时被这题题面唬住了，没想到原来这么简单/ll。
设第 \(i\) 个位置经过变化后的位置为 \(p_i\)。那么连边 \(i \to p_i\) 后所有环长的 \(\text{lcm}\) 为 \(K\)。
考虑先构造一组数 \(\{a_n\}\) 使得 \(\text{lcm}(a_1, a_2, \ldots, a_n) = K\) 且 \(\sum\limits_{i = 1}^n a_i\) 最小，\(a_i\) 表示第 \(i\) 个环的环长。结论是把 \(K\) 质因数分解后取 \(a_i = p_i^{e_i}\) 即可。
所以现在我们的任务是构造一些长度给定的环。考虑走 S 形拎出一条链（借用一下 Liquefyx 的图）：
所以我们如果可以交换相邻两个数，那么每次把链的第一个点逐个地交换到末尾即可。
写爆搜或者手玩可以得出交换相邻两个数的方案。于是这题就做完了。
131. CF1010E Store
想复杂了，其实蠢到家了/kk。
考虑一个包含全部 OPEN 点和询问点的长方体，如果长方体包含了 CLOSED 点那么这个询问就是 CLOSED。
只有询问点完全包含在全部 OPEN 点的长方体才是 OPEN。然后这题就做完了。
132. CF1010F Tree
educational 的。另一道类似的题是 [ABC269Ex] Antichain。
考虑令 \(b_u = a_u - \sum\limits_{v \in son_u} a_v\)。那么 \(\sum\limits_{i = 1}^n b_i = a_1 = x\)，且 \(\forall i \in [1, n], b_i \ge 0\)。所以最后连通块内有 \(y\) 个点，那么贡献系数为 \(\binom{x + y - 1}{y - 1}\)。所以转为计算包含 \(1\) 的连通块有 \(i\) 个点的方案数。
考虑经典树形背包，设 \(f_{u, i}\) 为 \(u\) 子树内包含 \(u\) 的连通块点数为 \(i\) 的方案数。特别地 \(f_{u, 0} = 1\) 表示转移上去断掉这条边。记 \(L, R\) 分别为 \(u\) 的左右儿子，有：
写成生成函数的形式，就是：
你发现这玩意直接做优化不了，因为 \(F_u(x)\) 的次数是 \(sz_u\) 级别的。这启发我们想到重链剖分。
具体地，考虑在重链顶处计算重链顶的多项式 \(F_u(x)\)。设重链上的点从浅到深依次为 \(a_1, a_2, \ldots, a_n\)，\(a_i\) 的轻儿子为 \(b_i\)（为了方便若没有轻儿子则 \(b_i = 0\)，\(F_0(x) = 1\)），我们有：
以此类推，设 \(G_i = x F_{b_i}(x)\)，那么 \(F_u(x) = G_1 (G_2(\ldots (G_n + 1)) \ldots + 1) + 1 = (\sum\limits_{i = 1}^n \prod\limits_{j = 1}^i G_j) + 1\)。
这个东西可以分治 NTT 计算。具体就是每次递归 \([l, r]\) 返回一个二元组 \((\sum\limits_{i = l}^r \prod\limits_{j = l}^i G_j, \prod\limits_{i = l}^r G_i)\)，那么 \([l, mid]\) 和 \([mid + 1, r]\) 的信息就可以合并了。
考虑每次计算的 \(G_i\) 次数之和为一棵树所有轻儿子的子树大小 \(= O(n \log n)\)，分治 NTT 再带两个 \(\log\)，总时间复杂度就是 \(O(n \log^3 n)\)。实际运行效率还可以。
133. CF995E Number Clicker
考虑取逆元相当于求了个随机数，所以直接双向 bfs 时间复杂度是对的。但是有更厉害的做法。
令 \(u \equiv \frac{a}{b} \pmod p\)，那么 \(-1\) 操作可以看成 \(u \to \frac{a - b}{b}\)，求逆元操作可以看成 \(u \to \frac{b}{a}\)。所以我们直接辗转相减可以让 \(u, v\) 都走到 \(0\)。
但是 \(100\) 的步数限制比较烦。考虑多随几个 \(b\) 直到走到 \(0\) 的步数 \(\le 100\)。看上去就很对。
134. [ABC269Ex] Antichain
和 CF1010F Tree 基本一致。
考虑经典树形背包，设 \(f_{u, i}\) 为 \(u\) 子树内选了 \(i\) 个点的方案数。初始有 \(f_{u, 0} = 1\)。每次考虑合并儿子 \(v\)，有转移：
最后有 \(f_{u, 1} \gets f_{u, 1} + 1\) 表示只选 \(u\)。
写成生成函数的形式，就是：
你发现这玩意直接做优化不了，因为 \(F_u(x)\) 的次数是 \(sz_u\) 级别的。这启发我们想到重链剖分。
具体地，考虑在重链顶处计算重链顶的多项式 \(F_u(x)\)。设重链上的点从浅到深依次为 \(a_1, a_2, \ldots, a_n\)，\(a_i\) 的所有轻儿子的 \(F_u(x)\) 的积为 \(b_i\)（为了方便若没有轻儿子则 \(b_i = 1\)），那么 \(b_i\) 可以分治 NTT 计算。然后有：
以此类推，可以得到 \(F_u(x) = b_1 (b_2(\ldots (b_n + x) \ldots) + x) + x = (\sum\limits_{i = 1}^{n - 1} x \prod\limits_{j = 1}^i b_j) + x\)。
这个东西可以分治 NTT 计算。具体就是每次递归 \([l, r]\) 返回一个二元组 \((\sum\limits_{i = l}^r \prod\limits_{j = l}^i b_j, \prod\limits_{i = l}^r b_i)\)，那么 \([l, mid]\) 和 \([mid + 1, r]\) 的信息就可以合并了。
考虑每次计算的 \(b_i\) 次数之和为一棵树所有轻儿子的子树大小 \(= O(n \log n)\)，分治 NTT 再带两个 \(\log\)，总时间复杂度就是 \(O(n \log^3 n)\)。可过。
135. CF1667E Centroid Probabilities
首先需要了解重心的三种定义：
- 删掉一个点后剩下子树大小 \(\le \frac{n}{2}\) 的点
- \(\sum\limits_{i = 1}^n \text{dis}(u, i)\) 最小的点
- 最深的 \(sz_u \ge \left\lceil\frac{n}{2}\right\rceil\) 的点
这道题我们使用第三种定义，也就是要统计 \(i\) 为最深的 \(sz_i \ge \left\lceil\frac{n}{2}\right\rceil\) 的点。
首先设 \(m = \left\lceil\frac{n}{2}\right\rceil\)。那么我们先计算 \(sz_i \ge m\) 的方案数 \(f_i\)。
枚举 \(sz_i = j\)，选点方案为 \(\binom{n - i}{j - 1}\)；子树内的点和子树外的点选父亲的方案数分别为 \((j - 1)!\) 和 \((n - j - 1)!\)，\(i\) 号点选父亲的方案为 \(i - 1\)。
所以：
考虑化成能快速算的形式。首先把和 \(i\) 有关的项提出来，消掉 \((j - 1)!\)，分母补一个 \((i - 2)!\)，有：
这不是组合数上指标求和吗。众所周知 \(\sum\limits_{i = m}^n \binom{i}{m} = \binom{n + 1}{m + 1}\)，所以：
现在 \(f_i\) 已经被化成能 \(O(1)\) 算的形式了。考虑再容斥计算答案。设 \(g_i\) 为 \(i\) 为最深的 \(sz_i \ge \left\lceil\frac{n}{2}\right\rceil\) 的点的方案数。枚举 \(i\) 子树内最深的 \(sz_i \ge \left\lceil\frac{n}{2}\right\rceil\) 的点为 \(j\)，我们有：
\(\frac{1}{i}\) 是 \(j\) 在 \(i\) 子树内的概率。考虑 \(j\) 不断跳父亲，跳到的第一个编号 \(\le i\) 的点在 \([1, i]\) 是等概率的。
所以维护一个后缀和就可以算 \(g_i\)。时间复杂度 \(O(n)\)。
136. QOJ7894 Many Many Heads
ucup 签到题。
考虑先任意求出一个合法括号序列。然后建出括号树。发现儿子有和父亲括号类型一样的就不行。并且儿子的括号类型不能有相同的。于是可以推出一定是形如不超过两条链的森林，并且两个根类型不同。然后就做完了。
137. QOJ836 Farm of Monsters
先把 \(h_i\) 全部减 \(1\)。设 \(a_i = \left\lfloor\frac{h_i \bmod B}{A}\right\rfloor + 1\) 表示若要获得 \(i\) 的得分要打多少次。\(b_i = \left\lfloor\frac{h_i}{B}\right\rfloor\) 表示对手要打多少次。
那么考虑一个序列 \(x_i = b_i - a_i - 1\) 或 \(x_i = b_i\)，\(x_i\) 表示打完第 \(i\) 个怪物后先手与后手的步数差值。因为是先手所以 \(x_0 = 1\)。那么 \(x\) 的前缀和 \(\ge 0\) 就合法。
考虑反悔贪心。一开始全部选 \(b_i - a_i - 1\)。一旦发现前缀和 \(< 0\) 就把前面 \(a_i + 1\) 最大的删了换成 \(b_i\)。正确性显然。时间复杂度 \(O(n \log n)\)。
138. P6681 [CCO2019] Bad Codes
被 QOJ1193 Ambiguous Encoding 撞了。
考虑直接 dp，设 \(f_{i, j}\) 为较长的串未被较短的串覆盖的部分是第 \(i\) 个字符串的长为 \(j\) 的后缀。转移考虑枚举接在较短的串后面是第 \(k\) 个串，然后讨论一下 \(j\) 和第 \(k\) 个字符串的大小关系就可以确定转移到哪。
发现转移成环，考虑建图用最短路转移。这里 \(|E| = n^2m, |V| = nm\)，复杂度看似是 \(O(|E| \log |V|) = O(n^2m \log nm)\) 的。但是 Dijkstra 最短路复杂度中的 \(|E|\) 实际上是松弛次数，但是这题考虑最大边权 \(\le m\) 所以任意时刻队列距离的极差 \(\le m\)，所以每个点松弛次数 \(\le m\)，所以复杂度其实是 \(O(n^2m + nm^2 \log nm)\)。这可以解释为什么 QOJ1193 Ambiguous Encoding 跑得那么快。
139. CF1427E Xum
vp 的时候随机化寄了，难过。
考虑不断构造 \(x\) 的最高位，这样可以不断消掉最高位直到 \(x\) 变为 \(1\)。
我们有这样的方案：
1a1 + 1a1 = 1a10
1a10 + 1a10 = 1a100
1a1 ^ 1a100 = 1a0a1
1a100 + 1a0a1 = 1a01a1
1a01a1 ^ 1a1 = 1a0000
1a100 + 1a100 = 1a1000
1a0000 ^ 1a1000 = 1000
这样我们构造出了 \(2^{\text{highbit}(x) + 1}\)。考虑用这个数去把 1a100 的除 \(\text{highbit}(x)\) 的位消掉，这样我们就得到了 \(2^{\text{highbit}(x)}\)。
好人类智慧啊/ll。
140. QOJ7737 Extending Distance
考虑平面图最短路转对偶图最小割，最小割转最大流。那么对于对偶图的每条边 \((u, v, w)\)，连 \((u, v, w, 0), (u, v, +\infty, 1)\)，那么就是要求一条流量为 \(dis + k\) 的流，使得费用最小。
直接跑费用流复杂度难以接受。考虑前 \(dis\) 单位流量的费用都是 \(0\)，所以先跑一遍最大流，然后在残量网络上再建新边即可。时间复杂度 \(O((nm)^3 + (nm)^2 k)\)。
141. P4565 [CTSC2018] 暴力写挂
考虑把其中一个 \(\text{dep}(\text{lca}(x, y))\) 去掉。答案的式子可以化成：
考虑建出边分树链，然后在第二棵树上 dfs，在 \(\text{lca}\) 处边分树合并统计不同子树的信息。
边分树链上每个点维护一个 \(g_u\) 表示子树内 \(\text{dis}(x, u) + \text{dep}(x)\) 的最大值。合并时，有 \(ans \gets \max(g_{ls_u} + g_{rs_v} - 2d, g_{ls_v} + g_{rs_u} - 2d)\)。然后更新 \(g_u \gets \max(g_u, g_v)\)。
时空复杂度均为 \(O(n \log n)\)。
142. CF757G Can Bash Save the Day?
考虑边分树可持久化，对于排列的一个前缀维护这些点的边分树链的并。查询直接跳边分树链即可。
边分树每个点维护子树点数和往左或右子树走的点到分治中心的距离之和。查询就跳一边计算另一边的贡献即可。
考虑交换排列的两个位置相当于重构两个前缀，直接重构即可。
时空复杂度均为 \(O((n + m) \log n)\)。
143. CF1656I Neighbour Ordering
首先显然每个点双独立，所以不同点双构造后直接合并即可。下面只考虑图点双连通的情况。
发现一个环显然有解。一个环加一条边也有解（例如 \((1, 2), (2, 3), (3, 4), (4, 1), (1, 3)\)）。
发现一个环连出去一条链再连回来就无解（例如 \((1, 2), (2, 3), (3, 4), (4, 1), (2, 5), (5, 4)\)）。
由此可见，图有哈密顿回路是有解的必要条件。
那么假设可以求出这个哈密顿回路，发现有两条交叉的边也无解了（例如 \((1, 2), (2, 3), (3, 4), (4, 1), (1, 3), (2, 4)\)）。所以图是一个平面图。进一步地，图是一个广义串并联图。
所以我们可以用缩二度点、叠重边的方法先把整个图缩成一条边（一个二元环）。然后把这个过程反过来变成加边，就能得到一条哈密顿回路。
然后发现此时一定有解。每个点的出边极角排序即可。
时间复杂度 \(O(n \log n)\)。
启示：若直接构造毫无思路，不妨考虑一些不能构造的情况，除去这些情况说不定会有很好的性质。
144. CF1091F New Year and the Mallard Expedition
神秘贪心不会做一点/ll。
我们考虑直接走，若 L 所需的能量不够了就从前面的 W 或 G 补充。
最后再考虑转化能量。考虑维护走 G 能转化的能量数，每个时刻这个数字都不能超过当前的能量值。然后从答案减去即可。
145. QOJ895 Color
神仙题。
相当于每个颜色有 \(\frac{m + 1}{2}\) 组匹配。特判掉一些显然无解的情况。
考虑记 \(c_{i, 0}\) 表示第 \(i\) 种颜色在 \([n + 1, m]\) 的点中还要多少对匹配，\(c_{i, 1}\) 表示在已有的点中有几个单点，\(c_{i, 2}\) 表示已有几对匹配。
若 \(c_{i, 1} + c_{i, 2} > \frac{m + 1}{2}\) 就无解，否则考虑网络流构造，从 \(n\) 个点的情况推到 \(n + 1\) 个点的情况。
左部点是 \(m\) 种颜色，右部点是 \(n + 1\) 个点，前 \(n\) 个点表示原图的点，最后一个点表示第 \(n + 1\) 个点暂时不选的颜色。若第 \(j\) 个点还没有第 \(i\) 种颜色就连边，左部点和右部点分别和源点、汇点连容量为 \(1\) 的边。特别地，第 \(i\) 个颜色向右部点的第 \(n + 1\) 个点连容量为 \(2 c_0\) 的点（这样可以保证二分图每个点度数相同，并且 \(c_0 = 0\) 时没有容量）。
正则二分图一定有完美匹配。于是我们可以从 \(n\) 推到 \(n + 1\)。一直推到 \(m + 1\) 就做完了。
146. CF995F Cowmpany Cowmpensation
考虑一个显然的树形 dp，设 \(f_{u, i}\) 为 \(u\) 结点染颜色 \(i\) 的方案数，有 \(f_{u, i} = \prod\limits_{v \in son_u} \sum\limits_{j = 1}^i f_{v, j}\)。前缀和后可得 \(f_{u, i} = f_{u, i - 1} + \prod\limits_{v \in son_u} f_{v, i}\)。
发现 \(f_u(x)\) 为最高次数为 \(sz_u\) 的多项式。考虑归纳证明，叶子结点有 \(f_u(x) = x\)。差分后是儿子的多项式乘积，次数为 \(\sum\limits_{v \in son_u} sz_v = sz_u - 1\)。前缀和后有次数为 \(sz_u\)。
于是树形 dp 算出 \(d = 1, 2, \ldots, n\) 的答案，拉格朗日插值即可。
时间复杂度 \(O(n^2)\)。
147. P7906 [Ynoi2005] rpxleqxq
考虑莫队二次离线。剩下是平衡插入和查询复杂度的问题。
考虑现在的问题：要求 \(O(\sqrt{n})\) 往集合里插入一个数，\(O(1)\) 回答集合内有多少个数 \(x\) 满足 \(z \oplus x \le m\)（\(z\) 给定）。
考虑高低位分块。先钦定 \(z\) 在前 \(9\) 位时 \(z \oplus x < m\)，枚举 \(z\) 的前 \(9\) 位更新答案；然后钦定 \(z\) 前 \(9\) 位 \(= m \oplus x\)，枚举 \(z\) 的后 \(9\) 位更新答案。查询是 \(O(1)\) 的。
总时间复杂度 \(O(n + (\sqrt{n} + \sqrt{q}))\)。
148. CF1017F The Neutral Zone
纯搞笑题。
显然每个质数的贡献可以直接算出来。但是内存限制不允许你直接筛质数。
但是你可以分块筛，\([k 10^6, (k + 1) 10^6 - 1]\) 一块，然后就做完了。
149. CF1017E The Supersonic Rocket
考虑求出两个点集的凸包，显然平移条件说明我们只用关心凸包的向量而不用关心点的具体位置。
为了处理可以旋转的条件，可以把这些向量按照“模长 - 角度 - 模长 - 角度”地拼成一个串，那么只用判两个串是否循环同构，把一个复制一遍然后 kmp 找子串即可。
算角度可以点乘除以两个向量的模长。
150. CF1017G The Tree
考虑没有 \(2\) 操作怎么做。
考虑减小一次修改的影响。发现我们 \(1\) 操作可以只单点 \(+1\)，查询就是 \(1 \to x\) 的链的最大后缀和是否 \(\ge 0\)。初始每个点权值为 \(-1\)。
考虑加入 \(2\) 操作怎么做。一个直观的想法是把 \(x\) 子树内的所有点权都赋为 \(-1\)。但是有可能出现 \(x\) 的祖先被加了很多次，导致全部赋为 \(-1\) 还是会被错判成黑色。解决办法是把 \(x\) 的权值减去 \(\text{x 到根的链的最大后缀和} + 1\)。
树剖 + 线段树维护，时间复杂度 \(O(n + q \log^2 n)\)。
151. [ABC338G] evall
考虑计算每个后缀的答案。分成 \(i\) 到最近一个 *，\(i\) 到最近一个 + 和 \(i\) 到末尾计算。
因为我懒了所以用线段树维护一个数字串的每个前缀读成的数的和。
152. CF1924B Space Harbour
不知道为什么好像大家在这题上花了挺久的。
发现对于一对相邻的港口 \((x_i, x_{i + 1})\)，\(x \in (x_i, x_{i + 1})\) 的花费是 \(y_i (x_{i + 1} - x)\)。拆开得 \(y_i x_{i + 1} - y_i x\)。
考虑用 set 维护所有港口，这样可以知道一个港口左边和右边的港口的坐标和价值。那么前一项 \(y_i x_{i + 1}\) 可以线段树区间覆盖，后一项 \(-y_i x\) 也可以线段树区间覆盖处理，相当于让一个代表 \([l, r]\) 区间的线段树结点的和变成 \(- y_i \frac{(l + r)(r - l + 1)}{2}\)。这个标记是可以下传的。
总时间复杂度为 \(O((m + q) \log n)\)。
153. CF1924D Balanced Subsequences
发现去掉匹配的 \(2k\) 个括号后，剩下的串一定形如 \()) \ldots )(( \ldots (\)，其中右括号数量为 \(a = m - k\)，左括号数量为 \(b = n - k\)。
考虑把剩下的串像 \()) \ldots ) \mid (( \ldots (\) 一样分成两半。枚举左半边加入了 \(\frac{i}{2}\) 对匹配，则长度为 \(a + i\)，右半边长度为 \(b + 2k - i\)。根据乘法原理把两半的方案数相乘即可。下面只讨论左半边的计算，右半边类似。
考虑折线图。相当于每一步可以向右上或右下走，求 \((0, 0) \to (a + i, -a)\) 且不接触直线 \(y = -a - 1\) 的方案数。这是经典问题。考虑容斥，总方案数 \(\binom{a + i}{a + \frac{i}{2}}\) 减去接触的方案数。把折线与 \(y = -a - 1\) 最后一个交点之前的部分对称过去，相当于 \((0, -2a - 2) \to (a + i, -a)\)。可以解得需要向右上走 \(a + \frac{i}{2} + 1\) 步，所以接触的方案数就是 \(\binom{a + i}{a + \frac{i}{2} + 1}\)。
注意为了避免算重，我们钦定左半边到达 \((a + i, -a)\) 是最后一次接触直线 \(y = -a\)。也就是说右半边除了第一步外不能接触直线 \(y = -a\)。钦定第一步向右上走后也可以类似地计算。
时间复杂度 \(O(\sum n + m + k)\)。
154. CF1924C Fractal Origami
对这种题一点办法都没有。。。
可以手动折叠发现 \(n = 3\) 时 \(M = 2 + 2 \sqrt{2}, V = 2 + 4 \sqrt{2}\)。于是大胆猜结论，第二次折叠开始，每次产生的山谷和山峰的长度相等。
为什么呢？考虑从第二次折叠开始，设当前纸的层数为 \(k\)（事实上若当前是第 \(i\) 次折叠，\(k = 2^{i - 1}\)）。则奇数层的纸展开后是山谷，偶数层的纸展开后是山峰。所以 \(V = M + 2 \sqrt{2}\) 恒成立。
这意味着我们只用计算 \(n\) 次折叠后的总折痕长度 \(V + M\)，就能算出 \(M\) 和 \(V\) 的值。考虑每次折叠，纸的每一层的折痕长度为上一次折叠时 \(\times \frac{1}{\sqrt{2}}\)，但是纸的层数为上一次折叠时 \(\times 2\)。所以每次折叠，总折痕长度为上一次的 \(\sqrt{2}\) 倍。于是 \(M = \sum\limits_{i = 0}^{n - 2} 2 \sqrt{2}^i, V = 2 \sqrt{2} + \sum\limits_{i = 0}^{n - 2} 2 \sqrt{2}^i\)。
至此直接套用等比数列求和公式 \(s = \frac{a (1 - q^n)}{1 - q}\) 即可出答案。由于需要快速幂，时间复杂度为 \(O(\sum \log n)\)。
实现时封装一个 \(a + b \sqrt{2}\) 的类会好写很多。
155. CF1924E Paper Cutting Again
印度出题人玩原神玩的吧？？？
考虑计算每条折线被选的概率。考虑相当于是有一个 \(1 \sim n + m - 2\) 的排列 \(p\)，然后一条 \(x = i\) 的直线被选且不是最后一个被选的，当且仅当它在 \(p\) 中排在 \(x = 1 \sim i - 1\) 和 \(y = 1 \sim \left\lfloor\frac{k}{i}\right\rfloor\) 之前。\(y = i\) 则类似。
一个 \(1 \sim N\) 的排列中，\(M\) 个数中一个数在其他 \(M - 1\) 个数前面的概率是 \(\frac{1}{M}\)。于是我们能很轻松地枚举每条 \(x = i\) 和 \(y = i\) 的直线计算答案。总时间复杂度 \(O(n + m)\)。
156. CF1197F Coloring Game
没啥意思的题。
考虑如何判定合法方案。考虑直接计算 sg 函数。
所以我们可以维护每个位置后面第 \(0, 1, 2\) 个位置的 sg 函数（显然 sg 值 \(\le 3\)），然后讨论第 \(i\) 个位置的颜色取值。显然没有限制的位置转移固定，可以矩阵快速幂优化。
但是复杂度 \(O(64^3 (n + m) \log V)\)，爆了。考虑预处理矩阵的 \(2^i\) 次幂，用向量乘矩阵即可优化到 \(O(64^3 \log V + 64^2 (n + m) \log V)\)。
157. CF1239E Turtle
放放/ll/ll/ll。
这题是个性质题。
首先第一排一定是升序，第二排一定是降序。考虑第一排若存在 \(i < j\) 使得 \(a_{1, i} > a_{1, j}\)，那么交换这两个数不会变劣。第二排类似。
然后发现在 \(1\) 走下去或在 \(n\) 走下去最优。考虑先求出从 \(1\) 走下去的答案 \(k\)，然后令 \(w_i = a_{1, i + 1} - a_{2, i}\)，那么从位置 \(x\) 走下去的答案就是 \(k + \sum\limits_{i = 1}^{x - 1} w_i\)。容易发现 \(w_i\) 单增，所以只可能在 \(1\) 或 \(n\) 处取到最值。
最后发现 \(a_{1, 1}, a_{2, n}\) 一定是最小值或次小值。若不是则把最小值（或次小值）交换过去不会变劣。
然后直接写个背包 dp，bitset 优化一下就完了。
时间复杂度 \(O(n^2 \sum a) = O(n^3 \max a)\)。
158. P5354 [Ynoi2017] 由乃的 OJ
考虑树剖套线段树，维护出每一位是 \(0\) 或 \(1\) 得到的结果是 \(0\) 还是 \(1\)。那么可以贪心求出答案，就是在不影响答案的前提下尽量填 \(0\)。
线段树维护上面那个东西显然可以开 \(k\) 个变量维护。观察到转移的形式都是一样的，所以可以把这 \(k\) 个变量压缩到一个 unsigned long long 里面，用位运算把转移变成 \(O(1)\)。
159. CF1158D Winding polygonal line
考虑限制相当于下一个点必须位于前两个点的直线的某一侧。
那么每次就选连成的直线最靠左（或最靠右）的点即可。
160. CF1142D Foreigner
考虑在一个排名为 \(k\) 的数后接上 \(c\)，新数的排名为 \(10 + c + \sum\limits_{i = 1}^{k - 1} i\)。
容易发现 \(\sum\limits_{i = 1}^{k - 1} i = \sum\limits_{i = 1}^{k \bmod 11 - 1} i\)。所以可以直接把 \(k \bmod 11\) 记到 dp 状态中。
具体就是，设 \(f_{i, j}\) 为以第 \(i\) 个位置结尾的，排名 \(\bmod 11 = j\) 的数的个数即可。
161. P9663 [ICPC2021 Macao R] Permutation on Tree
考虑转 01，枚举一个 \(x\)，令 \(a_i = [i \le x]\)，统计相邻不同对数。
设 \(f_u\) 为 \(u\) 子树的拓扑序个数，\(g_{u, i, 0/1}\) 表示 \(u\) 子树内拓扑序第 \(i\) 个点为 \(0/1\) 的方案数，\(h_{u, i, 0/1}\) 表示 \(u\) 子树内拓扑序第 \(i\) 和点和第 \(i + 1\) 个点值不同的方案数。
转移树形背包即可。\(g\) 的转移讨论合并后的子树拓扑序第 \(i\) 个点从原来哪棵子树来，\(h\) 的转移讨论合并后原来的相邻对是否破坏，若没破坏从哪棵子树来。时间复杂度 \(O(n^3)\)。
162. P4429 [BJOI2018] 染色
非常有趣的结论题。
首先显然，整个图不是二分图就无解。
然后显然每个连通块独立，可以分连通块判定。
然后发现一度点是没什么用的，因为无论和它相连的点颜色是什么，它都能找到一种和这种颜色不同的颜色。所以考虑类似拓扑排序剥一度点。剩下的图的 \(deg_u \ge 2\)。
考虑若有一个偶环 \(1 \to 2 \to 3 \to 4 \to 1\)，可以 \(\{A, B\}, \{A, B\}, \{B, C\}, \{A, C\}\)，容易发现这样可以钦定 \(1\) 号点染 \(B\)。
所以若有两个仅交于一点或者不交的偶环就寄了，因为通过钦定一定可以导出矛盾。
进一步地，若有两个不重合部分点数 \(\ge 2\) 的偶环就寄了，因为可以让不公共部分放 \(\{B, C\}, \{A, C\}\)，公共部分放 \(\{A, B\}\)，也可以导出矛盾。
考虑如何快速判断这个东西。
不妨研究一下这个图的度数特点。考虑若存在两个度数 \(\ge 3\) 的点 \(u, v\)，取出任意三条 \(u \to v\) 的路径 \(P_1, P_2, P_3\)。
考虑若两条路径 \(P_1, P_2\) 存在除 \(u, v\) 外的交点 \(w_1, w_2, \ldots, w_k\)，那么让 \(u \to w_1 \to u, v \to w_k \to v\) 即可构造出无解（此时认为路径在第一个点和最后一个点不重合）。
所以 \(P_1, P_2, P_3\) 一定两两不交。不妨设 \(|P_1| \le |P_2| \le |P_3|\)（定义路径长度为经过的边数）。有解当且仅当 \(|P_1| = |P_2| = 2\)。
考虑存在度数 \(\ge 4\) 的点也寄了，因为要么其他点度数都 \(\ge 2\)（此时为两个重合于一点的环），要么存在一个点度数 \(\ge 3\)。
所以有解的充要条件为：
- 不存在度数 \(\ge 4\) 的点；
- 不存在度数 \(\ge 3\) 的点，或存在且仅存在两个度数 \(\ge 3\) 的点 \(x, y\)，使得存在至少两个度数 \(= 2\) 的点连接 \(x, y\)。
163. P2435 染色
直接轮廓线 dp，设 \(f_{i, j, S}\) 为已经 dp 到 \((i, j)\) 这个格子，之前一行的状态为 \(S\)。转移枚举下一个格子的颜色即可。需要滚动数组。时间复杂度 \(O(nk^{m + 1})\)。
