CodeForces 887E Little Brother

洛谷传送门

CF 传送门

根据初中数学知识，圆心在 \(AB\) 线段的中垂线上。

又因为给定圆与 \(AB\) 线段所在直线不交，所以圆心在中垂线的一端极远处完全包含这个给定圆，在另一端极远处与这个给定圆相离。而具体在哪一端只与圆心在 \(AB\) 的左侧还是右侧有关。

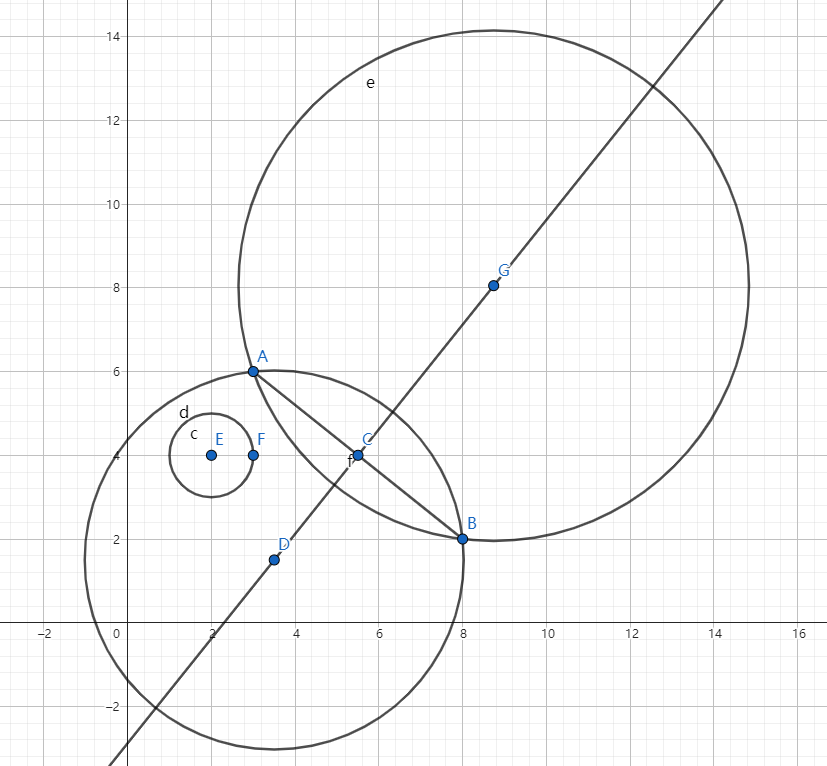
因此可以二分找到与给定圆外切和内切时圆心的坐标。那么一个给定圆只可能挡住一段连续的坐标。扫描线即可。

code

#include <bits/stdc++.h>
#define pb emplace_back
#define fst first
#define scd second
#define mkp make_pair
#define mems(a, x) memset((a), (x), sizeof(a))

using namespace std;
typedef long long ll;
typedef double db;
typedef unsigned long long ull;
typedef long double ldb;
typedef pair<ll, ll> pii;

const int maxn = 100100;

ll A, B, C, D, n, a[maxn], b[maxn], c[maxn];
ldb mx, my;

inline ldb calc(ldb x, ldb y) {
	return sqrtl(x * x + y * y);
}

void solve() {
	scanf("%lld%lld%lld%lld%lld", &A, &B, &C, &D, &n);
	mx = (ldb)(A + C) / 2;
	my = (ldb)(B + D) / 2;
	vector< pair<ldb, int> > vc;
	for (int i = 1; i <= n; ++i) {
		scanf("%lld%lld%lld", &a[i], &b[i], &c[i]);
	}
	if (B == D) {
		swap(mx, my);
		swap(A, B);
		swap(C, D);
		for (int i = 1; i <= n; ++i) {
			swap(a[i], b[i]);
		}
	}
	ldb kk = -(ldb)(A - C) / (B - D);
	ldb bb = my - mx * kk;
	ldb k1 = (ldb)(B - D) / (A - C);
	ldb b1 = my - mx * k1;
	for (int i = 1; i <= n; ++i) {
		if ((A != C && (b[i] - b1) / k1 > a[i]) || (A == C && A > a[i])) {
		// if (0) {
			ldb l = -2e12, r = 2e12;
			while (r - l > 1e-3) {
				ldb mid = (l + r) / 2;
				ldb x = mid, y = kk * mid + bb;
				ldb dis = calc(x - a[i], y - b[i]), R = calc(A - x, B - y);
				// printf("%.5Lf %.5Lf %.5Lf %lld %.5Lf\n", x, y, dis, c[i], R);
				if (dis + c[i] <= R) {
					l = mid;
				} else {
					r = mid;
				}
			}
			// printf("%.5Lf ", l);
			vc.pb(l, 1);
			r = 2e12;
			while (r - l > 1e-3) {
				ldb mid = (l + r) / 2;
				ldb x = mid, y = kk * mid + bb;
				ldb dis = calc(x - a[i], y - b[i]), R = calc(A - x, B - y);
				// printf("%.5Lf %.5Lf %.5Lf %lld %.5Lf\n", x, y, dis, c[i], R);
				if (dis <= R + c[i]) {
					l = mid;
				} else {
					r = mid;
				}
			}
			vc.pb(l, -1);
			// printf("%.5Lf\n", l);
		} else {
			// printf("i: %d\n", i);
			ldb l = -2e12, r = 2e12;
			while (r - l > 1e-3) {
				ldb mid = (l + r) / 2;
				ldb x = mid, y = kk * mid + bb;
				ldb dis = calc(x - a[i], y - b[i]), R = calc(A - x, B - y);
				// printf("%.5Lf %.5Lf %.5Lf %lld %.5Lf\n", x, y, dis, c[i], R);
				if (dis + c[i] >= R) {
					l = mid;
				} else {
					r = mid;
				}
			}
			// printf("%.5Lf ", l);
			vc.pb(l, -1);
			l = -2e12;
			while (r - l > 1e-3) {
				ldb mid = (l + r) / 2;
				ldb x = mid, y = kk * mid + bb;
				ldb dis = calc(x - a[i], y - b[i]), R = calc(A - x, B - y);
				// printf("%.5Lf %.5Lf %.5Lf %lld %.5Lf\n", x, y, dis, c[i], R);
				if (dis >= R + c[i]) {
					l = mid;
				} else {
					r = mid;
				}
			}
			vc.pb(l, 1);
			// printf("%.5Lf\n", l);
		}
	}
	vc.pb(mx, 0);
	sort(vc.begin(), vc.end());
	int x = 0;
	ldb ans = 1e18;
	for (auto p : vc) {
		if (!x) {
			// printf("x, y: %.5Lf %.5Lf\n", p.fst, kk * p.fst + bb);
			ans = min(ans, calc(A - p.fst, B - (kk * p.fst + bb)));
		}
		x += p.scd;
		if (!x) {
			// printf("x, y: %.5Lf %.5Lf\n", p.fst, kk * p.fst + bb);
			ans = min(ans, calc(A - p.fst, B - (kk * p.fst + bb)));
		}
	}
	printf("%.5Lf\n", ans);
}

int main() {
	int T = 1;
	// scanf("%d", &T);
	while (T--) {
		solve();
	}
	return 0;
}