AtCoder Beginner Contest 258 F Main Street
发现这题有个远古的 WA 就来改了(
发现走法很多种,不想分类讨论,考虑最短路。
设起点编号为 \(1\),终点为 \(11\)。
\(x = Bn\) 和 \(y = Bn\) 把坐标系分成了若干块。考虑过起点作一条平行于 \(Ox\) 的直线,与左右两条 \(x = Bn\) 的线有两个交点,给它们编号 \(3, 5\),同样地作一条平行于 \(Oy\) 的直线,与上下两条 \(y = Bn\) 的线有两个交点,给它们编号 \(4, 2\)。然后把起点所在块的四个角分别编号 \(6, 7, 8, 9\),然后连 \(1 \to 2, 3, 4, 5\),\(2, 3, 4, 5\) 再连到 \(6, 7, 8, 9\),像这样:
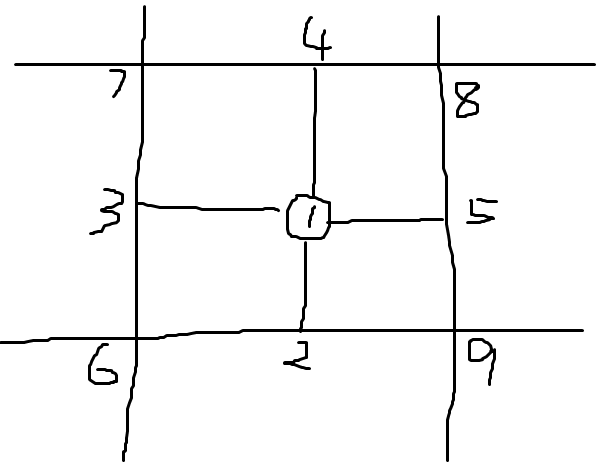
对于终点也是类似地建图,编号相对于起点 \(+ 10\)。
那对于起点和终点不在一个块的情况,先走到起点所在块的四个角的一个再走到终点所在块四个角的一个是一种备选方案。因此连边 \(x \to y + 10, x, y \in \{6, 7, 8, 9\}\),边权可以算出来。
在同一个块内,或者起点终点两个块相邻,可以不走到四个角,这个要特判,连相应的边。这里因为连边较复杂不展开,可以看代码。
然后跑一遍 \(1\) 到 \(11\) 的最短路就行。
code
#include <bits/stdc++.h>
#define pb push_back
#define fst first
#define scd second
using namespace std;
typedef long long ll;
typedef pair<ll, ll> pii;
ll B, K, sx, sy, ex, ey, head[30], len;
ll dis[30];
bool vis[30];
struct edge {
ll to, dis, next;
} edges[10000];
struct node {
ll dis, pos;
node() {}
node(ll a, ll b) : dis(a), pos(b) {}
bool operator < (const node &u) const {
return dis > u.dis;
}
};
void add_edge(ll u, ll v, ll d) {
// printf("%lld %lld %lld\n", u, v, d);
edges[++len].to = v;
edges[len].dis = d;
edges[len].next = head[u];
head[u] = len;
}
void solve() {
len = 0;
memset(head, 0, sizeof(head));
memset(dis, 0x3f, sizeof(dis));
memset(vis, 0, sizeof(vis));
scanf("%lld%lld%lld%lld%lld%lld", &B, &K, &sx, &sy, &ex, &ey);
ll sxb = (sx - 1) / B + 1, syb = (sy - 1) / B + 1;
ll exb = (ex - 1) / B + 1, eyb = (ey - 1) / B + 1;
add_edge(1, 2, (sy - (syb - 1) * B) * K);
add_edge(1, 3, (sx - (sxb - 1) * B) * K);
add_edge(1, 4, (syb * B - sy) * K);
add_edge(1, 5, (sxb * B - sx) * K);
add_edge(2, 6, sx - (sxb - 1) * B);
add_edge(2, 9, sxb * B - sx);
add_edge(3, 6, sy - (syb - 1) * B);
add_edge(3, 7, syb * B - sy);
add_edge(4, 7, sx - (sxb - 1) * B);
add_edge(4, 8, sxb * B - sx);
add_edge(5, 8, syb * B - sy);
add_edge(5, 9, sy - (syb - 1) * B);
add_edge(6, 7, B);
add_edge(6, 9, B);
add_edge(9, 6, B);
add_edge(9, 8, B);
add_edge(8, 9, B);
add_edge(8, 7, B);
add_edge(7, 8, B);
add_edge(7, 6, B);
// -----------------------------------
add_edge(12, 11, (ey - (eyb - 1) * B) * K);
add_edge(13, 11, (ex - (exb - 1) * B) * K);
add_edge(14, 11, (eyb * B - ey) * K);
add_edge(15, 11, (exb * B - ex) * K);
add_edge(16, 12, ex - (exb - 1) * B);
add_edge(19, 12, exb * B - ex);
add_edge(16, 13, ey - (eyb - 1) * B);
add_edge(17, 13, eyb * B - ey);
add_edge(17, 14, ex - (exb - 1) * B);
add_edge(18, 14, exb * B - ex);
add_edge(18, 15, eyb * B - ey);
add_edge(19, 15, ey - (eyb - 1) * B);
add_edge(16, 17, B);
add_edge(16, 19, B);
add_edge(19, 16, B);
add_edge(19, 18, B);
add_edge(18, 19, B);
add_edge(18, 17, B);
add_edge(17, 18, B);
add_edge(17, 16, B);
// -----------------------------------
add_edge(6, 16, (abs(sxb - exb) + abs(syb - eyb)) * B);
add_edge(6, 19, (abs(sxb - 1 - exb) + abs(syb - eyb)) * B);
add_edge(6, 17, (abs(sxb - exb) + abs(syb - eyb - 1)) * B);
add_edge(6, 18, (abs(sxb - 1 - exb) + abs(syb - eyb - 1)) * B);
add_edge(9, 16, (abs(sxb + 1 - exb) + abs(syb - eyb)) * B);
add_edge(9, 19, (abs(sxb - exb) + abs(syb - eyb)) * B);
add_edge(9, 17, (abs(sxb + 1 - exb) + abs(syb - eyb - 1)) * B);
add_edge(9, 18, (abs(sxb - exb) + abs(syb - eyb - 1)) * B);
add_edge(7, 16, (abs(sxb - exb) + abs(syb + 1 - eyb)) * B);
add_edge(7, 19, (abs(sxb - 1 - exb) + abs(syb + 1 - eyb)) * B);
add_edge(7, 17, (abs(sxb - exb) + abs(syb - eyb)) * B);
add_edge(7, 18, (abs(sxb - 1 - exb) + abs(syb - eyb)) * B);
add_edge(8, 16, (abs(sxb + 1 - exb) + abs(syb + 1 - eyb)) * B);
add_edge(8, 19, (abs(sxb - exb) + abs(syb + 1 - eyb)) * B);
add_edge(8, 17, (abs(sxb + 1 - exb) + abs(syb - eyb)) * B);
add_edge(8, 18, (abs(sxb - exb) + abs(syb - eyb)) * B);
// printf("%lld %lld %lld %lld %lld\n", sx, sy, ex, ey, K);
// -----------------------------------
if (sxb == exb && syb == eyb - 1) {
add_edge(4, 12, abs(sx - ex));
} else if (sxb == exb && syb == eyb + 1) {
add_edge(2, 14, abs(sx - ex));
} else if (sxb == exb - 1 && syb == eyb) {
add_edge(5, 13, abs(sy - ey));
} else if (sxb == exb + 1 && syb == eyb) {
add_edge(3, 15, abs(sy - ey));
}
if (sxb == exb && syb == eyb) {
add_edge(2, 12, abs(sx - ex));
add_edge(3, 13, abs(sy - ey));
add_edge(4, 14, abs(sx - ex));
add_edge(5, 15, abs(sy - ey));
}
add_edge(1, 11, (abs(sx - ex) + abs(sy - ey)) * K);
priority_queue<node> pq;
pq.push(node(0, 1));
dis[1] = 0;
while (pq.size()) {
int u = pq.top().pos;
pq.pop();
if (vis[u]) {
continue;
}
vis[u] = 1;
for (int i = head[u]; i; i = edges[i].next) {
ll v = edges[i].to, d = edges[i].dis;
if (dis[v] > dis[u] + d) {
dis[v] = dis[u] + d;
if (!vis[v]) {
pq.push(node(dis[v], v));
}
}
}
}
printf("%lld\n", dis[11]);
}
int main() {
int T = 1;
scanf("%d", &T);
while (T--) {
solve();
}
return 0;
}



