HDU 2073 无限的路

http://acm.hdu.edu.cn/showproblem.php?pid=2073

 

 

Problem Description

甜甜从小就喜欢画图画，最近他买了一支智能画笔，由于刚刚接触，所以甜甜只会用它来画直线，于是他就在平面直角坐标系中画出如下的图形：



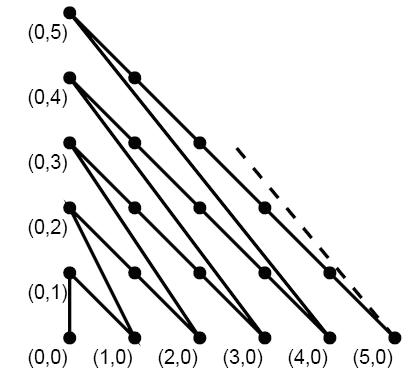
甜甜的好朋友蜜蜜发现上面的图还是有点规则的，于是他问甜甜：在你画的图中，我给你两个点，请你算一算连接两点的折线长度（即沿折线走的路线长度）吧。

 

Input

第一个数是正整数N（≤100）。代表数据的组数。
每组数据由四个非负整数组成x1，y1，x2，y2；所有的数都不会大于100。

 

Output

对于每组数据，输出两点(x1,y1),(x2,y2)之间的折线距离。注意输出结果精确到小数点后3位。

 

Sample Input

5

0 0 0 1

0 0 1 0

2 3 3 1

99 99 9 9

5 5 5 5

 

Sample Output

1.000

2.414

10.646

54985.047

0.000

 

代码：

#include <bits/stdc++.h>
using namespace std;

double A(int x,int y) {
    if(x == 0 && y == 0)
        return 0.0;
    if(x == 0 && y == 1)
        return 1.0;
    if(x != 0)
        return A(x - 1 , y + 1) + sqrt(2.0);
    else
        return A(y - 1, 0) + sqrt(y * y * 1.0 + (y - 1.0) * (y - 1.0));
}

int main() {
    int N, x1, x2, y1, y2;
    scanf("%d", &N);
    for(int i = 1; i <= N; i ++) {
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        printf("%.3lf\n", fabs(A(x1, y1) - A(x2, y2)));
    }
    return 0;
}