N 皇后问题
N 皇后
【题目】
N 皇后问题是指在 N*N 的棋盘上要摆 N 个皇后,要求任何两个皇后不同行、不同列,也不在同一条斜线上。给定一个整数 n,返回 n 皇后的摆法有多少种。
例子:
n=1,返回 1
n=2或3,返回 0
n=8,返回 92
【分析】
以行为单位进行判断,这样做的好处是,不需要考虑皇后共行的问题,只需要考虑共列或者共斜线的问题。
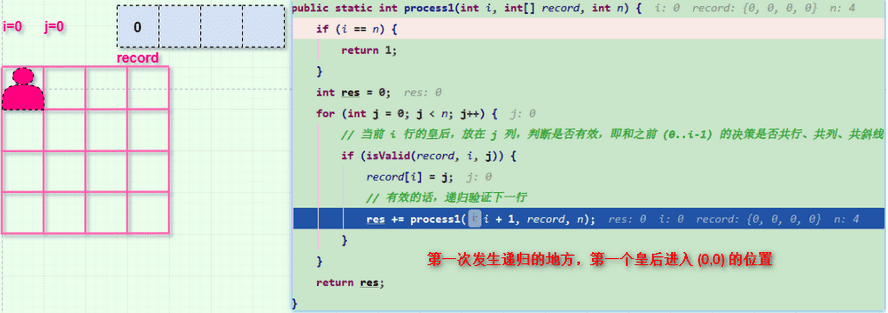
上面在第一行 (0, 0)的位置放置了第一个皇后之后,开始判断第二行的位置
依次判断 (1, 0)(共列) 、(1, 1)(共斜线)
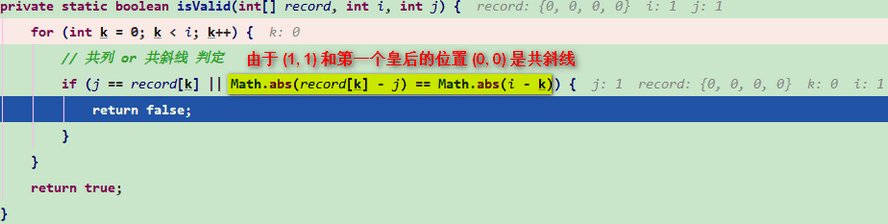
等到了 (1, 2),找到了第二个皇后的位置,找到之后,进行递归调用,找第三个皇后的位置
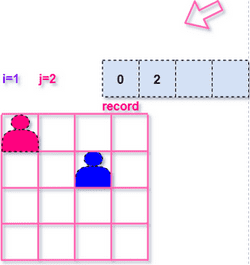
依次判断第三行的各个位置,发现都没有第三个皇后的立足之地,当前递归函数结束,返回到上一层调用处,即 (1, 2) 的位置,这说明当前的决策有问题,第二个皇后需要调整位置,找到了 (1, 3) 的位置,修改相关变量:
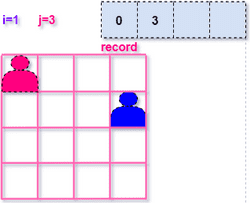
基于当前的决策,继续向下进行递归调用,即判断第三行皇后的位置。和上面的流程一样,找到了 (2, 1) 的位置
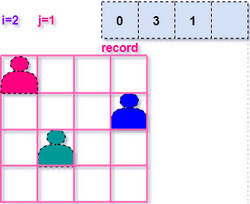
继续往下层递归调用,寻找第四个皇后的位置。通过一轮验证,发现第四行四个位置都没有皇后的合适位置,当前递归函数结束,返回到上一层,即 (2, 1) 的位置,从 (2, 2) 继续往后验证。
通过一轮验证,发现第三行剩余位置都没有皇后的合适位置,则说明当前决策有问题,当前递归过程结束,返回到上一层递归函数,即 (1, 3) 的位置,由于第二行已经是验证完毕,没有位置了,说明第二行的决策也有问题,返回到上一层递归函数,即 (0, 0) 的位置。
第一个皇后从 (0, 1) 的位置决策,重复上面描述的步骤。
代码如下:
public class Code19_NQueens {
public static void main(String[] args) {
int n = 4;
System.out.println(num1(4));
}
public static int num1(int n) {
// base case
if (n < 1) {
return 0;
}
// 记录皇后的位置,数组下标表示行,值表示列
int[] record = new int[n];
return process1(0, record, n);
}
/**
* @param i 来到了第 i 行
* @param record recode[0..i-1] 表示之前的行,放了的皇后的位置,即已经决策好的
* @param n 代表整体一共有多少行 0~n-1
* @return 摆完所有的皇后,合理的摆法有多少种
*/
public static int process1(int i, int[] record, int n) {
if (i == n) {
return 1;
}
int res = 0;
// j 代表列
for (int j = 0; j < n; j++) {
// 当前 i 行的皇后,放在 j 列,判断是否有效,即和之前 (0..i-1) 的决策是否共行、共列、共斜线
if (isValid(record, i, j)) {
record[i] = j;
// 有效的话,递归验证下一行
res += process1(i + 1, record, n);
}
}
return res;
}
/**
* 验证 (i, j) 位置是否和之前的决策共列或共斜线
*/
private static boolean isValid(int[] record, int i, int j) {
for (int k = 0; k < i; k++) {
// 共列 or 共斜线 判定
if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {
return false;
}
}
return true;
}
}
在此基础上改造了 leetcode 51 题
class Solution {
public List<List<String>> solveNQueens(int n) {
if (n < 1) {
return new ArrayList<>();
}
List<List<String>> res = new ArrayList<>();
// 记录皇后的位置,数组下表表示行,值表示列
int[] record = new int[n];
process1(0, record, n, res);
return res;
}
/**
* @param i 来到了第 i 行
* @param record recode[0..i-1] 表示之前的行,放了的皇后的位置,即已经决策好的
* @param n 代表整体一共有多少行 0~n-1
* @return
*/
public void process1(int i, int[] record, int n, List<List<String>> res) {
if (i == n) {
res.add(new ArrayList<String>(assemblePos(record)));
}
// j 代表列
for (int j = 0; j < n; j++) {
// 当前 i 行的皇后,放在 j 列,判断是否有效,即和之前 (0..i-1) 的决策是否共行、共列、共斜线
if (isValid(record, i, j)) {
record[i] = j;
// 有效的话,递归验证下一行
process1(i + 1, record, n, res);
}
}
}
private List<String> assemblePos(int[] record) {
char[][] temp = new char[record.length][record.length];
for (int i = 0; i < temp.length; i++) {
for (int j = 0; j < temp[0].length; j++) {
temp[i][j] = '.';
}
}
for (int i = 0; i < record.length; i++) {
temp[i][record[i]] = 'Q';
}
List<String> ans = new ArrayList<>();
for (char[] chars : temp) {
ans.add(new String(chars));
}
return ans;
}
/**
* 验证 (i, j) 位置是否和之前的决策共列或共斜线
*/
private boolean isValid(int[] record, int i, int j) {
for (int k = 0; k < i; k++) {
// 共列 or 共斜线 判定
if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {
return false;
}
}
return true;
}
}
代码优化
使用位运算进行代码的优化
需要准备三个变量,作为位运算的容器,比如 Java 中 int 可以用 32 bit 来表示,1 表示这个位置不可以放置皇后,0 表示这个位置可以放置皇后。
三个变量 colLimit、leftDiaLim、rightDiaLim 分别限制列、左斜线、右斜线在 N 皇后的期盼上面有没有放置限制。
举个例子:
假设我们在 N*N 的棋盘的第一行,(0, 4) 的位置,放置了一个皇后。则 colLimit 这个相应的 bit 位置应该设置为 1,表示这个列已经不可以再放置皇后了。
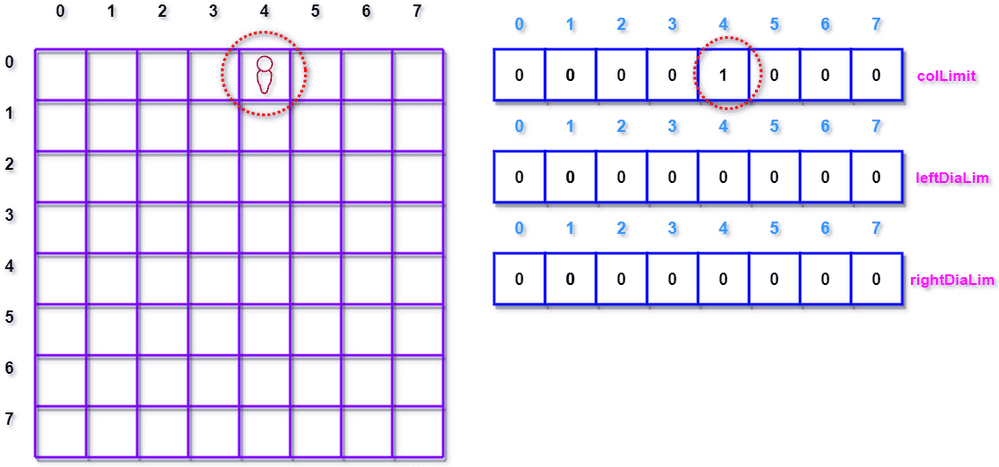
再考虑 leftDiaLim 和 rightDiaLim 该如何处理呢?
对于第二行,应该是 (1, 3) 和 (1, 5) 两个位置不能放置皇后,因为其和 (0, 4) 位置在同一条对角线上面。所以 leftDiaLim 在 colLimit 的基础上左移一位即可,rightDiaLim 在 colLimit 的基础上右移一位即可。如下图:
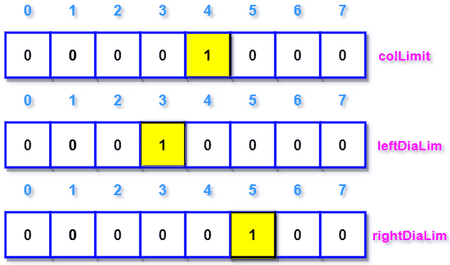
当判断第二行的哪些位置可以放置皇后的时候,只需要将上面的三个变量进行 | 运算即可得到哪些位置可以尝试放置皇后。
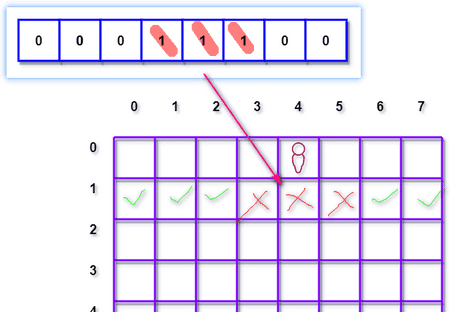
假设,第二个皇后放置到了 (1, 1) 的位置,则对于第三行来说,不可放置的位置如下图所示:

对于 colLimit 变量好处理,即在相应的位置标记为 1 即可。
而对于 leftDiaLim 来说,第一行 (0, 4) 的皇后对第三行的左对角线上的影响,相对于之前是向左移动了一位,第二行皇后 (1, 1) 对第三行的影响还是左下左移一位,所以总体来说 leftDiaLim 需要左移一位。rightDiaLim 同理需要右移一位。最后的数据如下图:
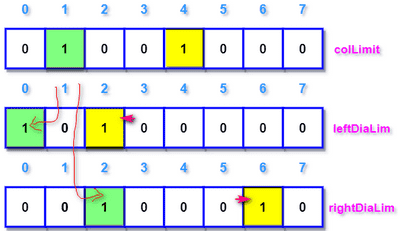
当判断第三行的哪些位置可以放置皇后的时候,只需要将上面的三个变量进行 | 运算即可得到哪些位置可以尝试放置皇后。
……
以后的步骤都是如此,,,
代码如下:
/**
* 使用位运算优化
*/
public static int num2(int n) {
if (n < 1 || n > 32) {
return 0;
}
// 如果是 n 皇后问题,limit 最右是 n 个 1,其他都是 0(32 个 1 的话,值是 -1)
int limit = n == 32 ? -1 : (1 << n) - 1;
return process2(limit, 0, 0, 0);
}
/**
* @param limit 划定问题的规模,几皇后问题?固定变量
* @param colLimit 列的限制,1 的位置表示不能放皇后,0 的位置表示可以放皇后
* @param leftDiaLim 左斜线的限制
* @param rightDiaLim 右斜线的限制
* @return
*/
private static int process2(int limit, int colLimit, int leftDiaLim, int rightDiaLim) {
// corner case
if (colLimit == limit) {
return 1;
}
// 总的限制(解决左侧超出问题规模的 1 的干扰),结果是每一个 1 的位置是可以放皇后的
int pos = limit & (~(colLimit | leftDiaLim | rightDiaLim));
int mostRightOne = 0;
int res = 0;
// 尝试 post 中所有的 1
while (pos != 0) {
// 提出 post 中,最右侧的 1,即放皇后的位置
mostRightOne = pos & (~pos + 1);
pos = pos - mostRightOne;
res += process2(limit, colLimit | mostRightOne, (leftDiaLim | mostRightOne) << 1, (rightDiaLim | mostRightOne) >>> 1);
}
return res;
}
上面代码中有几个点需要补充说明下:
代码中有 limit 变量是用来控制问题的规模,也是利用的二进制位表示,比如 8 皇后问题,最右是 8 个 bit 全是 1,左边全是 0,9 皇后问题,右边 9 个 bit 全是 1,左边全是 0,……,如果达到 32 bit 全是 1,则对应的只就是 -1。
int pos = limit & (~(colLimit | leftDiaLim | rightDiaLim)); 这行代码,是处理二进制位左侧对于程序的影响,又利用了 limit 控制里问题的规模。最后计算出来的二进制,只需要尝试位置为 1 的 bit 位即可。
尝试所有 bit 位为 1 的逻辑是:
int mostRightOne = 0;
// 尝试 post 中所有的 1
while (pos != 0) {
// 提出 post 中,最右侧的 1,即放皇后的位置
mostRightOne = pos & (~pos + 1);
pos = pos - mostRightOne;
……
}
递归的执行上面的流程。
【时间复杂度】
由于每一行都要尝试 N 次,一共 N 行,所以时间复杂度是 O(N*N)



