Paper Reading - Convolutional Sequence to Sequence Learning ( CoRR 2017 ) ★

Link of the Paper: https://arxiv.org/abs/1705.03122

Motivation:

• Compared to recurrent layers, convolutions create representations for fixed size contexts, however, the effective context size of the network can easily be made larger by stacking several layers on top of each other. This allows to precisely control the maximum length of dependencies to be modeled. Convolutional networks do not depend on the computations of the previous time step and therefore allow parallelization over every element in a sequence. This contrasts with RNNs which maintain a hidden state of the entire past that prevents parallel computation within a sequence.
• Multi-layer convolutional neural networks create hierarchical representations over the input sequence in which nearby input elements interact at lower layers while distant elements interact at higher layers. Hierarchical structure provides a shorter path to capture long-range dependencies compared to the chain structure modeled by recurrent networks. Inputs to a convolutional network are fed through a constant number of kernels and non-linearities, whereas recurrent networks apply up to n operations and non-linearities to the first word and only a single set of operations to the last word. Fixing the number of nonlinearities applied to the inputs also eases learning.

Innotation:

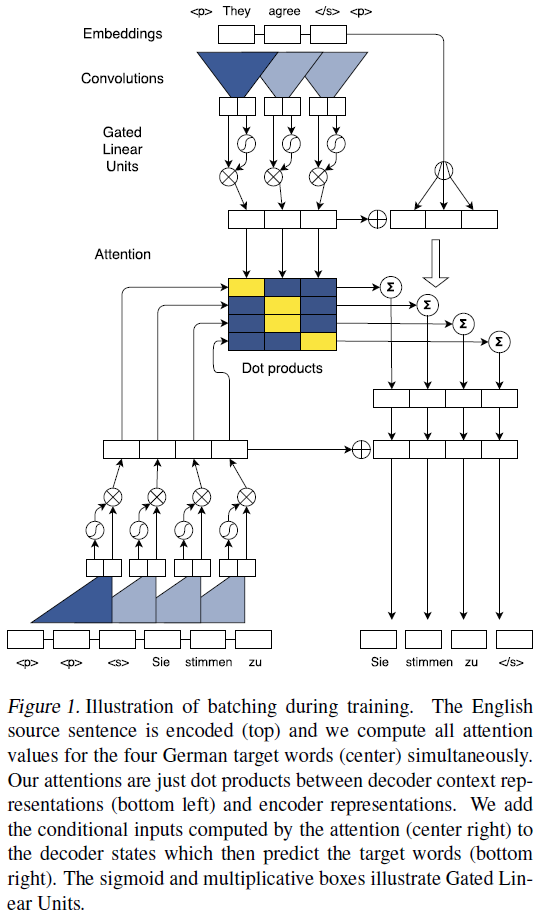
• An architecture for Seq2Seq modeling based entirely on convolutional neural networks. Both encoder and decoder networks share a simple block structure that computes intermediate states based on a fixed number of input elements. Each block contains a one dimensional convolution followed by a non-linearity. For a decoder network with a single block and kernel width k, each resulting state h_i¹ contains information over k input elements. Stacking several blocks on top of each other increases the number of input elements represented in a state. ( Stacking is similar to the pooling process. )
• Position Embeddings: Input elements x = (x₁, . . . , x_m) embedded in distributional space as w = (w₁, . . . , w_m), where w_j ∈ R^f is a column in an embedding matrix D ∈ R^V×f. The authors also equip the model with a sense of order by embedding the absolute position of input elements p = (p₁, . . . , p_m) where p_j ∈ R^f. Both are combined to obtain input element representations e = (w₁+p₁, . . . , w_m+p_m). Position embeddings are useful in the architecture since they give the model a sense of which portion of the sequence in the input or output it is currently dealing with.
• The authors introduce a separate attention mechanism for each decoder layer.

Improvement:

• The model is equipped with gated linear units ( Language modeling with gated linear units - Dauphin et al., arXiv 2016 ) and residual connections ( Deep Residual Learning for Image Recognition - He et al., CVPR 2015a ). 
  • The authors choose gated linear units as non-linearity which implement a simple gating mechanism over the output of the convolution Y = [A B] ∈ R^2d: v([A  B]) = A  ⓧ σ(B), where A, B ∈ R^d are the inputs to the non-linearity, ⓧ is the point-wise multiplication and the output v([A B]) ∈ R^d is half the size of Y. The gates σ(B) control which inputs A of the current context are relevant. And GLUs perform better than tanh in the context of language modelling.
  • To enable deep convolutional networks, authors add residual connections from the input of each convolution to the output of the block. h_i^l = v( W^l [h_i−k/2^l−1, . . . , h_i+k/2^l−1] + b_w^l ) + h_i^l−1 
• For encoder networks authors ensure that the output of the convolutional layers matches the input length by padding the input at each layer. However, for decoder networks they have to take care that no future information is available to the decoder. Specifically, we pad the input by k − 1 elements on both the left and right side by zero vectors, and then remove k elements from the end of the convolution output.

General Points:

• Sequence to sequence modeling has been synonymous with recurrent neural network based encoder-decoder architectures. The encoder RNN processes an input sequence x = (x₁, . . . , x_m) of m elements and returns state representations z = (z₁, . . . , z_m). The decoder RNN takes z and generates the output sequence y = (y₁, . . . , y_n) left to right, one element at a time. To generate output y_i+1, the decoder computes a new hidden state h_i+1 based on the previous state h_i, an embedding g_i of the previous target language word y_i, as well as a conditional input c_i derived from the encoder output z. Models without attention consider only the final encoder state z_m by setting c_i = z_m for all i, or simply initialize the first decoder state with z_m, in which case c_i is not used. Architectures with attention compute c_i as a weighted sum of (z₁, . . . , z_m) at each time step. The weights of the sum are referred to as attention scores and allow the network to focus on different parts of the input sequence as it generates the output sequences. Attention scores are computed by essentially comparing each encoder state z_j to a combination of the previous decoder state h_i and the last prediction y_i; the result is normalized to be a distribution over input elements.