深度理解普里姆算法的贪心策略

在求解MST的普里姆和克鲁斯卡尔两个算法中都用到了贪心的策略，贪心一直是一个比较不好想且不好证明的算法。

这里就以普里姆算法为例详细的介绍一下它是怎么贪的。

首先我们需要知道普里姆算法的基本过程就是从某一点开始开始，不断的从未选择的点的集合U中选出能到达集合V（即为MST的顶点的集合）的最小权值的点，直到这个集合包含了所有的节点，也就是一个贪心过程，集合V指的就是已经被选入为最小生成树的点的集合。

那么首先我们以两个点为例，如下图所示

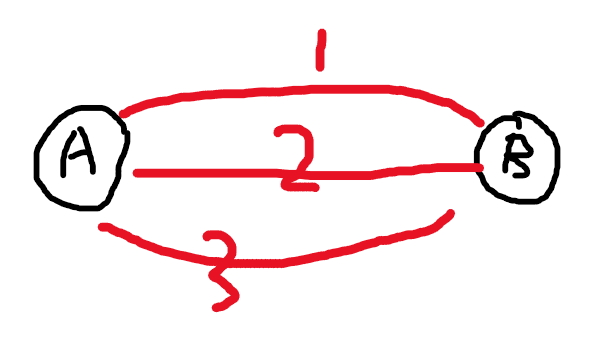
 那么我们可以很明显的知道这个最小生成树就是A-B并且选权值为1的点，这就是最优解。

那么N个点其实也是一样，我们只要把集合U和集合V看成是两个点，就好理解了，比如说起点到第一个点为例

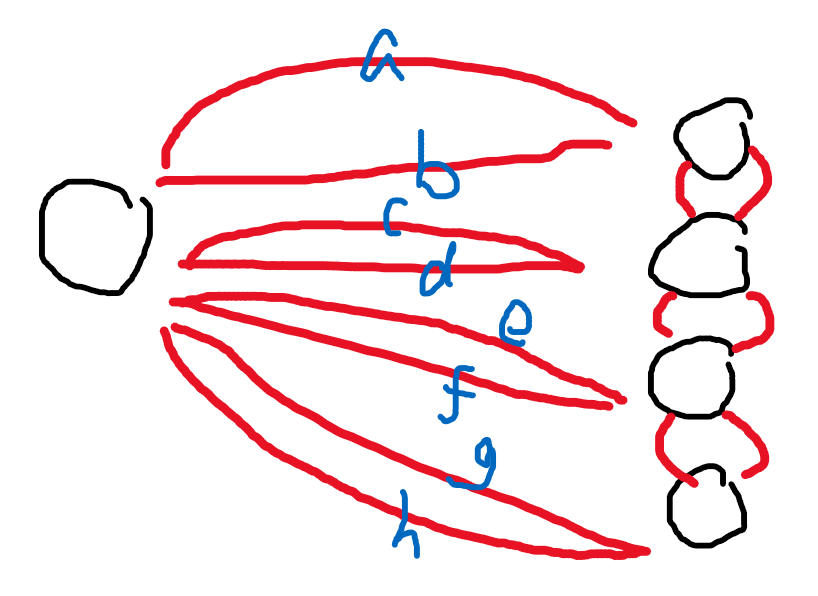
 那么从这个图为例，我们以左边的点作为起点，在abcdefg中我们应该选择哪一条边呢，我们可以把右边的4个点看成是一个整体，也就是看成是一个点，这个图就会变成这样

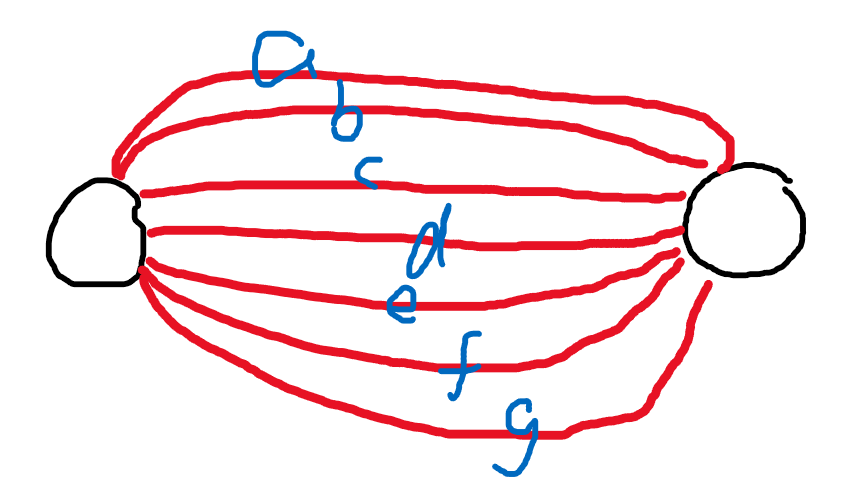
 这个图和我们的第一张图就很像了，我们只要选这7条边中最短的一条就可以了，那么我们假设a最短，这个图就会变成这样(b没用了，就不用管它)

 那么第三个点我们应该怎么找呢（左边为集合V，右边为集合U），跟前面一样，只要把左边看成一个点，右边看成一个点，就可以得到下面这个图

 然后我们只要选所有边中最短的一条就行了。之后就是不断的用这种方法，直到把所有的点都放到左边这个集合，那么MST就找到了。

那么我们就把找MST的每一步都看成是求两个点之间的最短路，每两个点之间都是最短路，也就是每一步都是最优解，那么所有点构成的当然就是最小生成树了，这就是普里姆算法的贪心思想。

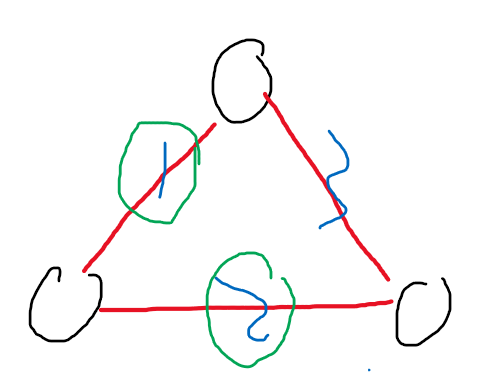
为了进一步证明这个结论，我们再举两个例子（为了方便观察，两点之间只有一条边，因为多的也没用，肯定选最少的）

三个点之间找MST

四个点的MST

 

  我们可以看到两个MST中的每一条边对每一个点来说，都是权值较小的边。

也就是说，把这些点任意分成两个集合，那么MST的边一定是连接这两个集合中权值最小的边。