2020牛客寒假算法训练营第一场题解(持续更新中)
这一题要求计算格点图中”好三角形“的数量。好三角形是面积为1,至少有一条边平行于x轴或y轴,并且顶点都在格点上的三角形。
那么我们可以分两种情况考虑,分别为同时平行于x轴和y轴以及只有一条边平行。
第一种情况很简单,在每个1*3的矩形中都有4个,那么在n*m的矩形中一共有(m-2)*(n-1)+(n-2)*(m-1)种这样的不同矩形,所以就有((m-2)*(n-1)+(n-2)*(m-1))*4个矩形。
第二种情况又可以分为两种情况,分别为底为2高为1和底为1高为2两种情况。
以底为2高为1为例,设x轴为m,y轴为n,这里需要注意的就是不要与第一种情况重复。
如果底与x轴平行,我们可以得到(m-2)*n个不同的底,对于每个底来说,只需要选择第三个点即可,因为第三个点选择的时候不能构成直角三角形,否则会重复,所以对于每一个底,只能选择(m-2)个点作为其顶点,然后对于每一行来说,都可以往上取或者往下取,但是由于最下面一行只能往上取和最上面一行只能往下取,所以我们把这两行合并,最后就得到这样的三角形有((m-2)*(m-2)*(n-1))*2个,那么以y轴为底就有((n-2)*(n-2)*(m-1))*2个。
同理可得,以底为1的三角形分别有((m-1)*(m-2)*(n-2))*2和((n-1)*(n-2)*(m-2))*2个。最后只要把这5种全部加起来就行了。
在这里我犯了一个非常低级的错误,那就是取模。写这个题解也就是要提醒自己以后不要犯一样的错误。下面是错误示范

ll ans=0; ans+=((m-2)*(n-1)+(n-2)*(m-1))*4%mod; ans+=((m-2)*(m-2)*(n-1))*2%mod; ans+=((n-2)*(n-2)*(m-1))*2%mod; ans+=((m-1)*(m-2)*(n-2))*2%mod; ans+=((n-1)*(n-2)*(m-2))*2%mod; cout<<ans%mod<<endl;
一定要记得,取模一定要对每一个元素都要取模!!!!以下为AC代码

#include <iostream> using namespace std; #define ll long long ll mod=1000000007; int main() { ll n,m; cin>>n>>m; ll ans=0; ans+=(((m-2)%mod*(n-1))%mod+((n-2)*(m-1)%mod))*4%mod; ans+=((m-2)%mod*(m-2)%mod*(n-1)%mod)*2%mod; ans+=((n-2)%mod*(n-2)%mod*(m-1)%mod)*2%mod; ans+=((m-1)%mod*(m-2)%mod*(n-2)%mod)*2%mod; ans+=((n-1)%mod*(n-2)%mod*(m-2)%mod)*2%mod; ans%=mod; cout<<ans<<endl; return 0; }
一个算数学期望的水题,知道数学期望就能做,就直接上代码了

#include<iostream> int main() { double n,x,a,b; scanf("%lf%lf%lf%lf",&n,&x,&a,&b); printf("%.2f",n*((x/100.00)*a+(1-x/100.00)*b)); }
这个题是一个不是很明显的矩阵快速幂,关于矩阵快速幂的问题我在别的博客已经讲过,这里就不讲,我们可以看到给的递推式为
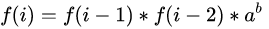
由于ab是一个常数,我们把这个常数设为t,那么我们首先写一下前几项,可以很轻易的得到
f(1)=x f(2)=y f(3)=xyt f(4)=xy2t2 f(5)=x2y3t4 f(6)=x3y5t7 f(7)=x5y8t12
然后我们分别看x,y以及t的系数,我们看到他们的系数随着n的变换形成的是斐波那契额数列,如果我们把斐波那契额的第n项设为feb(n)的话
那么我们可以得到f(n)的表达式为
f(n)=xfeb(n-2)yfeb(n-1)t(feb(n-2)+feb(n-1)-1)
由于x,y,t均为常数,所以要想求f(n),我们只需要求出斐波那契的数列的第n-1项和第n-2项即可。
求斐波那契的第n项是个非常经典的矩阵快速幂,我们只要设矩阵为
1 1 2 1 3 2 5 3
1 0 那么对其2次方为 1 1 三次方为 2 1 四次方为 3 2
根据矩阵快速幂我们可以很快的得到,但是这里还有一点就是要利用费马小定理




