组合数，快速幂，取模。

例题

题目来源：

http://acm.hdu.edu.cn/contests/contest_showproblem.php?pid=1007&cid=843

组合数的性质（参考于以下博客）

https://blog.csdn.net/litble/article/details/75913032

组合数的通项公式

组合数的递推公式（重要）

 

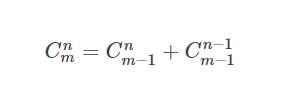
一些重要的公式

 

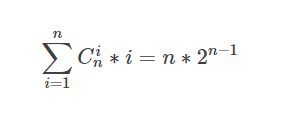
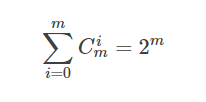
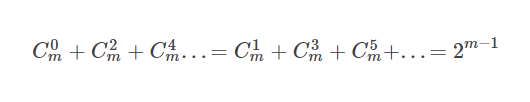
一般的公式

 

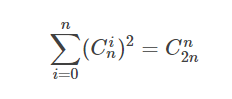
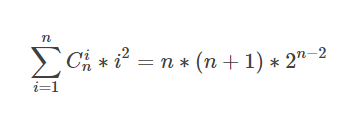
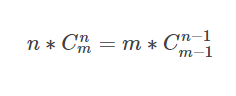
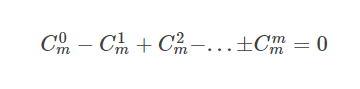
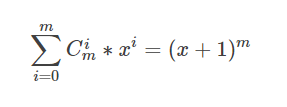
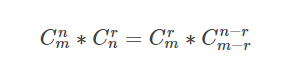
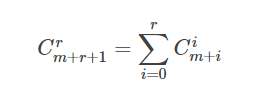
快速幂（取模）（代码出自以下网站，但略有修改）

 https://blog.csdn.net/dbc_121/article/details/77646508

ll a,b,mod;
ll Mode(ll a,ll b)
{
  if(b==0)
  return 1%mod;
  ll sum=1;
  a=a%mod;
  while(b>0)
  {
    if(b%2==1)
    sum=(sum*a)%mod;
    b/=2;
    a=(a*a)%mod;
    }
  return sum;
}

解题思路

 先通过组合数的性质推出公式为（n-1）*2^n+1,然后根据快速幂取模求解。

完整代码

#include<iostream>
#include<stdio.h>
#define m 1000000007
using namespace std;
long long Mode(long long a,long long b)
{
    long long sum=1;
    a=a%m;
    while(b>0)
    {
        if(b%2==1)
        sum=(sum*a)%m;
        b/=2;
        a=(a*a)%m;
    }
    return sum;
}

int main()
{
    long long num,n;
    while(scanf("%lld",&n)!=EOF)
    {
        num=(((n-1)%m*Mode(2,n))%m+1)%m;
        printf("%lld\n",num);
    }
    return 0;
}