134. 加油站

labuladong 题解思路

难度中等

1270

在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

给定两个整数数组 gas 和 cost ，如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则 保证 它是 唯一 的。

 

示例 1:

输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
因此，3 可为起始索引。

示例 2:

输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发，因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发，可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站，此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站，此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站，因为返程需要消耗 4 升汽油，但是你的油箱只有 3 升汽油。
因此，无论怎样，你都不可能绕环路行驶一周

 

class Solution:
    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
        start = cur_sum = min_sum = 0
        n = len(gas)
        for i in range(n):
            cur_sum+= gas[i]-cost[i]
            if cur_sum < min_sum:
                min_sum = cur_sum
                start = i+1
        if cur_sum < 0:
            return -1 
        return start

 

暴力：

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
       
        for (int a = 0; a <gas.size();a++) {
            if (gas[a]<cost[a]) continue;
            int remains = 0;
            for(int step = 0; step < gas.size();step++) {
                int i = (step+a)%gas.size();
                remains += gas[i];
                remains -= cost[i];
                if (remains<0) {break;}
            }
            if (remains>=0) {
                return a;
            } 

        }
        return -1;
    }
};

 

思路1：

 对于站点 i，我们把 gas[i] - cost[i] 当作整体考虑，我们用diff[i] = gas[i] - cost[i] 表示从当前站点出发，到下一个站点后剩余的油量。

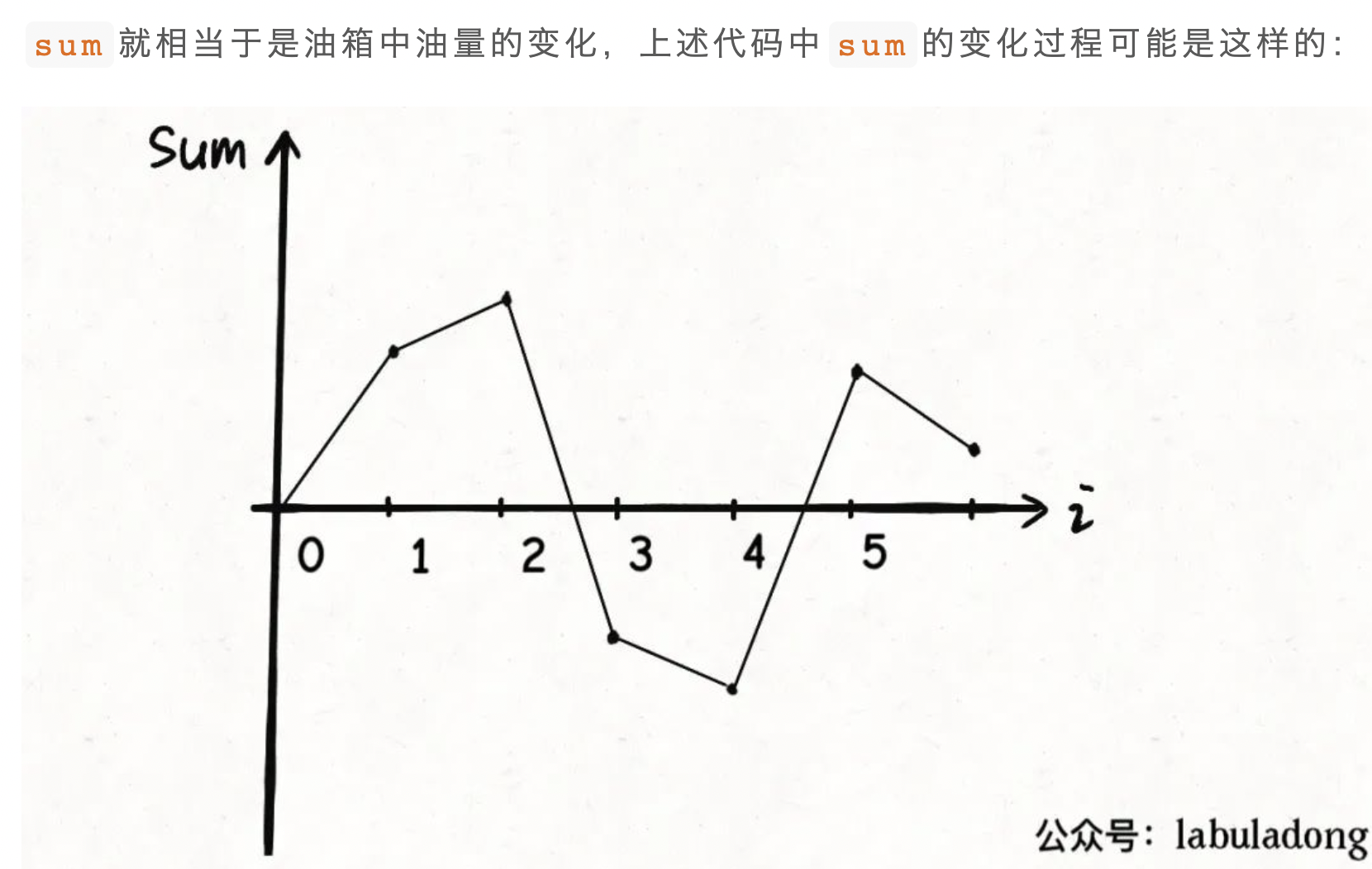
题目就是需要找出这么一个点，从这个点出发，diff的累加值能达到峰值。

这道题就是求diff[]数组上的 和最大连续子序列，这个最大子序列的起始点就是车的出发点！如果车从这儿开都不能做到油箱不空，那么这个题目就该返回-1了。

因此，这道题转化成了 求循环数组的最大子序列问题。

 

思路2：

基于一个数学定理：

如果一个数组的总和非负，那么一定可以找到一个起始位置，从他开始绕数组一圈，累加和一直都是非负的

有了这个定理，判断到底是否存在这样的解非常容易，只需要把全部的油耗情况计算出来看看是否大于等于0即可。

那么如何求开始位置在哪？

注意到这样一个现象：

1. 假如从位置i开始，i+1，i+2...，一路开过来一路油箱都没有空。说明什么？说明从i到i+1，i+2，...肯定是正积累。
2. 现在突然发现开往位置j时油箱空了。这说明什么？说明从位置i开始没法走完全程(废话)。那么，我们要从位置i+1开始重新尝试吗？不需要！为什么？因为前面已经知道，位置i肯定是正积累，那么，如果从位置i+1开始走更加没法走完全程了，因为没有位置i的正积累了。同理，也不用从i+2，i+3，...开始尝试。所以我们可以放心地从位置j+1开始尝试。

 

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int diff=0;
        for(int i=0;i<gas.length;i++)
            diff+=gas[i]-cost[i];
        if(diff<0) return -1;
        
        
        int start =0;
        int sum = 0;
        for(int i =0;i<gas.length;i++){
            if(sum<0){
                sum = gas[i]-cost[i];
                start = i;
            }
            else
                sum+=gas[i]-cost[i];
        }
        return start;
    }   
}