198. House Robber(动态规划)

198. House Robber

You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.

Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.

Example 1:

Input: [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
             Total amount you can rob = 1 + 3 = 4.

Example 2:

Input: [2,7,9,3,1]
Output: 12
Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
             Total amount you can rob = 2 + 9 + 1 = 12.

 

 

 

如果两个相邻的房子在同一个晚上被打破，它将自动联系警察。

 

dfs

class Solution {
public:
    int dfs(int end, vector<int>& nums) {
        if (end < 0) return 0;
        int res = 0;
        for(int i = 0; i <= end;i++) {
            res  = max(res, nums[i] + dfs(i-2,nums));
        }
        return res;
    }
    int rob(vector<int>& nums) {
        return dfs(nums.size()-1,nums);
    }
};

 

 

 

记忆化

class Solution {
public:
    int dfs(int end, vector<int>& nums,vector<int>& dp) {
        if (end < 0) return 0;
        if (dp[end]!=-1) return dp[end];
        int res = 0;
        for(int i = 0; i <= end;i++) {
            res  = max(res, nums[i] + dfs(i-2,nums,dp));
        }
        dp[end] = res;
        return res;
    }
    int rob(vector<int>& nums) {
        vector<int> dp(nums.size(),-1);
        return dfs(nums.size()-1,nums,dp);
    }
};

 

 

 

class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp (n+1,0);
        dp[1] = nums[0];
        if (n <= 1) return dp[n];
        dp[2] = max(nums[0],nums[1]);
        for(int i = 2;i <=n; ++i) {
            dp[i] = max(dp[i-2] + nums[i-1],dp[i-1]);  
        }
        return dp[n];
    }
};

 

 

 

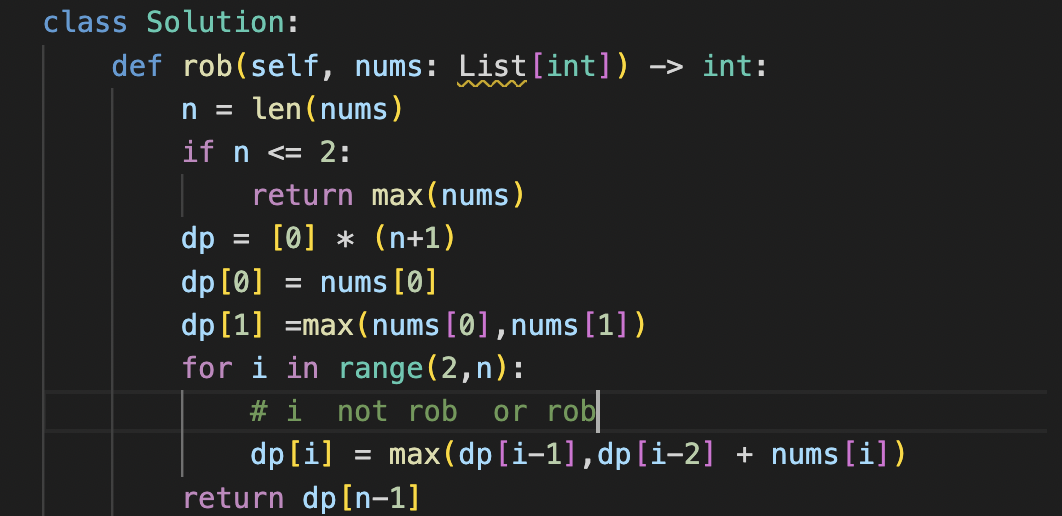
 1 class Solution:
 2     def rob(self, nums):
 3         """
 4         :type nums: List[int]
 5         :rtype: int
 6         """
 7         n = len(nums)
 8         if n==0:
 9             return 0
10         if n==1 :
11             return nums[0]
12         dp=[0]*n
13         dp[0] =nums[0]
14         dp[1] = max(nums[0],nums[1])
15         for i in range(2,n):
16             dp[i] = max(dp[i-2]+nums[i],dp[i-1])
17         return dp[n-1]
18

 

 

 1 class Solution {
 2 public:
 3     int rob(vector<int>& nums) {
 4         int n = nums.size();
 5         if(n==0) return 0;
 6         if(n==1) return nums[0];
 7         if(n==2) return std::max(nums[0],nums[1]);
 8         vector<int> dp(n,0);
 9         dp[0] = nums[0];
10         dp[1] = std::max(nums[0],nums[1]);
11         for(int i = 2;i<n;i++)
12             dp[i] = std::max(dp[i-1],nums[i]+dp[i-2]);
13         return dp[n-1];
14     }
15 };

 

posted @ 2018-04-09 17:50  乐乐章  阅读(157)  评论(0)  编辑  收藏  举报